Скорости точек твердого тела. Угловая скорость тела.
Скорость любой точки тела определяется в неподвижном базисе:
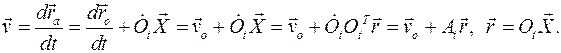
Матрица 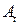 есть антисимметричная матрица, что доказывается так:
есть антисимметричная матрица, что доказывается так: 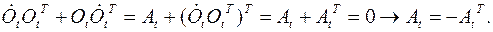
Тогда получим
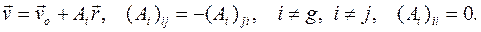
Вектор 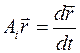 можно представить следующим образом:
можно представить следующим образом:
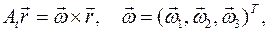
так как
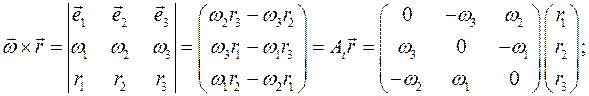
где три различных элемента матрицы 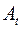 , по определению, образуют вектор угловой скорости твердого тела
, по определению, образуют вектор угловой скорости твердого тела 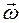 :
:
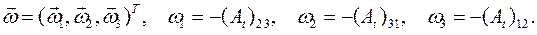
Тогда скорость точки тела вычисляется как векторная сумма скорости поступательного движения 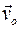 с выбранным началом подвижной системы координат О и скорости вращательного движения
с выбранным началом подвижной системы координат О и скорости вращательного движения 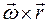 :
:
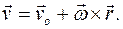
Вектор угловой скорости 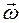 не зависит от выбора полюса О и определяется только матрицей вращения
не зависит от выбора полюса О и определяется только матрицей вращения 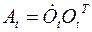 .
.
Связь скоростей любых двух точек А и В тела.
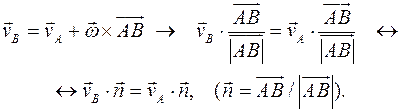
Таким образом, проекции скоростей любых двух точек твердого тела 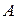 и
и 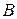 на направление вектора
на направление вектора 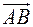 , соединяющего точки, равны.
, соединяющего точки, равны.
Положение и движение любой точки твердого тела при поступательном движении тела.
Поступательное движение тела имеет три степени свободы из шести, так как элементы матрицы вращений постоянны, а вектор 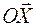 тоже постоянен для всех точек тела и его будем считать нулевым, взяв начало подвижной системы координат в центре масс тела (его положение в теле всегда можно определить). Поэтому все точки тела в любом его положении имеют одинаковые скорости и одинаковые ускорения, а траектории всех точек тела имеют одинаковую форму.
тоже постоянен для всех точек тела и его будем считать нулевым, взяв начало подвижной системы координат в центре масс тела (его положение в теле всегда можно определить). Поэтому все точки тела в любом его положении имеют одинаковые скорости и одинаковые ускорения, а траектории всех точек тела имеют одинаковую форму.
Введем неподвижную ортогональную систему координат с координатами x , y, z и началом О. Для простоты обозначений абсолютное положение некоторой точки тела 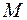 обозначим вектором положения точки
обозначим вектором положения точки
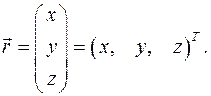
Движение точки тела определяется изменением её положения во времени:
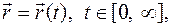
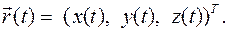
Скорость точки тела есть вектор 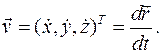
Компоненты вектора скорости есть производные по времени от компонент вектора движения.
Ускорение точки тела есть вектор 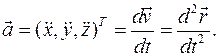
Компоненты вектора ускорения есть производные по времени от компонент вектора скорости.
Компоненты векторов скорости и ускорения (проекции векторов) записаны в декартовом базисе.
Траектория точки есть геометрическое место всех последовательных положений точки при ее движении:
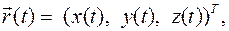
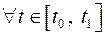 .
.
Дата добавления: 2020-05-20; просмотров: 542;











