Оптическая активность. Искусственная анизотропия
1. Оптическая активность. В 1811 году Франсуа Араго, изучая прохождение линейно поляризованного света через кварц, установил, что в ряде случаев плоскость поляризации вышедшего из кварца луча поворачивалась по сравнению с вошедшим на некоторый угол. Способность среды вызывать вращение плоскости поляризации проходящего через нее света назвали оптической активностью среды.
Подробно исследовал оптическую активность Жан Био в 1815 году. Он обнаружил наличие оптической активности помимо твердых тел в растворах (сахар в воде) и в парах некоторых органических веществ. Био установил закон: угол поворота плоскости поляризации пропорционален толщине слоя активного вещества и концентрации этого вещества в растворе. j = [a]∙l∙c Закон Био, 1815(20.1)
| Таблица 20.1 | |||
| Вещество | Растворитель | с, % | a, град/дм |
| Сахар С12Н22О11 | Вода | +68 | |
| Глюкоза С6Н12О6, a | Вода | +112 | |
| Фруктоза С6Н12О6, b | Вода | –132 | |
| Хинхонин С19Н22ОN2 | Спирт | 0,735 | +264 |
| Хинидин С20Н24О2N2 | Спирт | 0,77 | +243 |
| Хинин С20Н24О2N2 | Спирт | 2,0 | –169 |
| Камфора С10Н16О, d | Спирт | +44 | |
| Никотин С10Н14N2 | Вода | –79 |
Здесь [a] - удельная оптическая активность.
В таблице 20.1 с – весовая концентрация, т.е. концентрация растворенного вещества в граммах на 100 г раствора. Все значения удель-ной активности [a] приведены при l = 589,3 нм и температуре 293 К в свеже-приготовленных растворах. Для чистых веществ (скипидар, кварц) формула закона Био записывается в виде: j = a∙l. (20.2)
Здесь a - удельное вращение на единицу длины. Некоторые вещества оптически активны лишь в кристаллическом состоянии. Например кварц (a = ±21,7 град/мм), соль NaClO3 (a = ±21,2 град/мм). Их оптическая активность есть свойство кристалла в целом и называется структурной. Другие веществ активны в любом агрегатном состоянии. Это значит, что их оптическая активность определяется свойствами отдельных молекул.
Направление вращения у разных веществ неодинаково. Если свет, идущий в глаз наблюдателя, поворачивает плоскость колебаний вектора 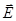 по часовой стрелке, то вещество называют правовращающим (луч «выглядит» как левый винт, a записывают со знаком «+»). Если свет закручивается против часовой стрелки, вещество называют левовращающим (луч – правый винт, a со знаком «–»). Все оптически активные вещества существуют в двух модификациях – правовращающей и левовращающей.
по часовой стрелке, то вещество называют правовращающим (луч «выглядит» как левый винт, a записывают со знаком «+»). Если свет закручивается против часовой стрелки, вещество называют левовращающим (луч – правый винт, a со знаком «–»). Все оптически активные вещества существуют в двух модификациях – правовращающей и левовращающей.
2. Нормальная и аномальная оптическая активность. В первом случае удельное вращение a растет с уменьшением длины волны l по приближенному закону (Био, 1815):

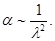 Нормальная активность (20.3)
Нормальная активность (20.3)
В случаях аномальной оптической активности, которая была открыта позднее, удельное вращение примерно пропорционально длине волны: 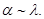 Аномальная активность (20.4)
Аномальная активность (20.4)
Оба вида оптической активности присущи любому оптически активному веществу. Нормальная оптическая активность наблюдается при l, сильно отличающихся от длины волны lо, при которых в оптически активном веществе происходит резонансное поглощение. Аномальная активность наблюдается при l вблизи lо.
3. Теория оптической активности Френеля. В 1823 году Френель предложил феноменологическую теорию оптической активности. Она состоит в следующем.
Линейно поляризованная волна ведет себя в оптически активном веществе так, как если бы она состояла из двух волн, поляризованных по кругу в противоположных направлениях, с одинаковыми частотами и амплитудами (рис.173-а).
Если скорости распространения обеих волн не одинаковы, то по мере прохождения света через вещество один из векторов 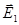 или
или 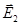 будет отставать. В результате плоскость колебаний суммарного вектора
будет отставать. В результате плоскость колебаний суммарного вектора 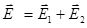 будет поворачиваться (рис.173-б).
будет поворачиваться (рис.173-б).
 Не имея возможности доказать гипотезу теоретически (не было уравнений Максвелла), Френель доказал ее экспериментально. Для этого он сконструировал призму, состоящую из трех призм. Две крайние призмы сделаны из правовращающего кварца, средняя – из левовращающего (рис.174).
Не имея возможности доказать гипотезу теоретически (не было уравнений Максвелла), Френель доказал ее экспериментально. Для этого он сконструировал призму, состоящую из трех призм. Две крайние призмы сделаны из правовращающего кварца, средняя – из левовращающего (рис.174).
Оптические оси АА всех призм совпадают с направлением падающего на сложную призму луча. Этот луч, не преломляясь на грани АВ (угол падения 0°), на границе призм АМ расщепляется на два луча, поляризованных по кругу.
Луч с правым вращением (на рис.174 внизу) имеет в первой призме меньший показатель преломления nп, чем луч с левым вращением (nл), nп < nл. В левовращающей призме соотношение меняется nп > nл. Поэтому на границе АМ лучи испытывают разное преломление. Правый луч отклоняется к стороне AD, а левый – к стороне ВС. На гранях МD и СD это расхождение еще более усиливается.
В результате из призмы выходят два луча, угол между которыми составляет около 4 минут. Исследование с помощью четвертьволновой пластинки показало, что верхний луч поляризован по правому, а нижний – по левому кругу.
Таким образом Френель доказал, что при вступлении в оптически активную среду луч света испытывает двойное круговое лучепреломление. Лучи, поляризованные по правому и по левому кругу, идут внутри оптически активной среды с разными фазовыми скоростями.
Если падающий свет был линейно поляризован, то при выходе из такой среды эти волны снова слагаются в линейно поляризованную волну с повернутой плоскостью поляризации.
4. Круговой дихроизм состоит в том, что коэффициенты поглощения двух волн, циркулярно поляризованных во взаимно перпендикулярных направлениях, различны.
В отличие от линейного дихроизма, наблюдающегося в двояко преломляющих кристаллах, круговой дихроизм наблюдается в оптически активных средах. Если линейный дихроизм используется в поляроидах для преобразования естественного света в линейно поляризованный, то круговой дихроизм может использоваться для преобразования естественного света в циркулярно поляризованный. Однако на практике удобнее линейные поляризаторы с четвертьволновыми пластинками.
5. Фотоупругость. Так называется явление возникновения оптической анизотропии под действием механических напряжений. Фотоупругость открыли в 1813 году Томас Зеебек и независимо от него в 1816 году Дейвид Брюстер.
Причина фотоупругости состоит в том, что под действием механических напряжений упорядочивается ориентация оптически анизотропных молекул или их частей, а также деформируются электронные оболочки атомов и молекул. В результате однородное в обычных условиях вещество при механических напряжениях приобретает свойства двояко преломляющего кристалла. Для малых одноосных растяжений или сжатий выполняется закон Брюстера: Dn = ne – no= Г∙s Закон Брюстера, 1815 (20.5)
 Здесь s – нормальное напряжение, Г– упругооптическая постоянная (постоянная Брюстера). Для стекол Г = 10–12÷10–11 м2çН, для целлулоида Г = 10–11÷10–10 м2çН.
Здесь s – нормальное напряжение, Г– упругооптическая постоянная (постоянная Брюстера). Для стекол Г = 10–12÷10–11 м2çН, для целлулоида Г = 10–11÷10–10 м2çН.
Схема опыта для излучения фотоупругости такая же, как схема для наблюдения двойного лучепреломления в кристаллах. Она включает в себя источник света S, поляризаторы П1 и П2 и деформируемое тело (рис.175). Обычно плоскости пропускания анализаторов взаимно перпендикулярны и образуют с осью напряжений MN углы 45о.
Деформируемое тело приобретает свойства одноосного кристалла, оптическая ось которого совпадает с направлением деформации MN.
Показатель преломления ne соответствует волне, вектор Ее которой колеблется вдоль оси напряжений MN, а показатель nо – волне, вектор Ее которой колеблется поперек оси MN.
Разность ne – no может быть положительной и отрицательной в зависимости от материала. Кроме того, она зависит от длины волны l (дисперсия двойного преломления). Поэтому при наблюдении в белом свете при скрещенных поляризаторах деформируемое тело окрашивается в разные цвета. Фотоупругость используется при изучении напряжений в механических конструкциях, расчет которых очень сложен. Исследование сводится к измерению анизотропии, возникающей под действием нагрузок в модели, изготовленной из прозрачного материала, с учетом критериев подобия.
6. Эффект Фарадея. В 1845 году Майкл Фарадей обнаружил поворот плоскости поляризации света в веществах, помещенных в магнитное поле и в обычных условиях не являющихся оптически активными. Это было первое явление, в котором выявилась связь между оптическими и электромагнитными процессами. Схема установки на рис.176.
 Линейно поляризованный свет, выходящий из поляризатора П1, проходит через отверстие электромагнита и далее через исследуемое тело К так, чтобы направление луча совпадало с направлением магнитных силовых линий. Установив поляризатор П2 на темноту в отсутствии поля, при включении поля можно обнаружить поворот плоскости поляризации.
Линейно поляризованный свет, выходящий из поляризатора П1, проходит через отверстие электромагнита и далее через исследуемое тело К так, чтобы направление луча совпадало с направлением магнитных силовых линий. Установив поляризатор П2 на темноту в отсутствии поля, при включении поля можно обнаружить поворот плоскости поляризации.
Если наблюдатель смотрит вдоль силовых линий магнитного поля (рис.176), то вращение вправо плоскости поляризации луча, идущего в глаз наблюдателя, считается положительным, влево – отрицательным. Если свет идет перпендикулярно линиям магнитного поля, то образец К ведет себя как одноосный двояко преломляющий кристалл, оптическая ось которого параллельна линиям поля.
Опыты самого Фарадея, а затем более точные опыты М. Верде показали, что угол поворота плоскости поляризации пропорционален длине l пути света в веществе и магнитной индукции поля В. j = VBl. Закон Верде, 50-ые годы 19 века. (20.6)
| Таблица 20.2 | ||
| Вещество | 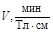
| |
| Газы | ||
| Азот N2 | 6,92×10–2 | |
| Воздух | 6,83×10–2 | |
| Гелий He | 0,72×10–2 | |
| Кислород О2 | 3,14×10–1 | |
| Жидкости | ||
| Азот N2 | 4,15×101 | |
| Бензин | 3,0×102 | |
| Бензол C6H6 | 2,1×104 | |
| Вода H2O | 1,3×102 | |
| Спирт эт. C2H5OH | 1,1×102 | |
| Твердые тела | ||
| Стекло крон | 1,7×102 | |
| Стекло флинт | 8,9×102 | |
| Кварц | 1,7×102 | |
| NaCl, кристалл | 3,3×102 | |
| ZnS, кристалл | 2,8×103 | |
Коэффициент пропорциональности V называют удельным магнитным вращением или коэффициентом Верде. В таблице 20.2 приведены значения постоянной Верде для некоторых веществ при l = 589 нм.
Величина V в таблице соответствует углу поворота плоскости поляризации в угловых минутах на одном сантиметре при индукции поля 1 Тл при температуре 20оС.
Углы поворота очень невелики. Вычислим для примера угол j поворота в опытах Фарадея, который использовал в работе стеклянный параллелепипед размером 2´2´0,5 дюймов из боросиликатного крона. Отсюда l = 5 см, V = 1,7∙102 мин/Тл×см. Если допустить, что магнитное поле в опытах Фарадея было умеренным и его индукция В составляла в диэлектрике (в стекле) 0,01 Тл, получаем j = V×l×B = 1,7∙102∙5∙0,01 = 8,5 угловых минут.
Но поскольку направление вращения зависит от направления магнитного поля по отношению к направ-лению луча, то эффект можно усилить за счет много-кратного прохождения луча в активной зоне. Эту воз-можность реализовал еще Фарадей, который посеребрил противоположные грани стеклянного образца (рис.177).
 Заметим, что такой возможности нет в случае естественной оптической активности, поскольку луч поворачивается все время в одну сторону. Отразившись от зеркала, он идет по тому же поляризационному пути и возвращается в исходное состояние. Направление вращения положительно у диамагнетиков и отрицательно у пара-магнетиков. Например, в растворе FeCl3 V = –2,03∙105 мин/Тл×см.
Заметим, что такой возможности нет в случае естественной оптической активности, поскольку луч поворачивается все время в одну сторону. Отразившись от зеркала, он идет по тому же поляризационному пути и возвращается в исходное состояние. Направление вращения положительно у диамагнетиков и отрицательно у пара-магнетиков. Например, в растворе FeCl3 V = –2,03∙105 мин/Тл×см.
7. Электрооптический эффект Керра. В 1875 году Джон Керр открыл явление двойного лучепреломления в обычно однородном диэлектрике, помещенном в электрическое поле. В результате эффекта Керра жидкость или газ в электрическом поле приобретают свойства одноосного кристалла, оптическая ось которого направлена вдоль поля.
Для наблюдения эффекта Керра естественный монохроматический свет пропускают через поляризатор П1 и направляют в плоский конденсатор, заполненный обычно анизотропным веществом, например, нитробензолом (рис.178). Кювету К с жидкостью и конденсатором называют ячейкой Керра.
 Если к обкладкам конденсатора не приложено напряжение, то поляризация света, проходящего через вещество ячейки Керра, не меняется. Свет полностью гасится анализатором П2, плоскость пропускания которого перпендикулярна плоскости пропускания поляризатора П1.
Если к обкладкам конденсатора не приложено напряжение, то поляризация света, проходящего через вещество ячейки Керра, не меняется. Свет полностью гасится анализатором П2, плоскость пропускания которого перпендикулярна плоскости пропускания поляризатора П1.
Если к обкладкам конденсатора приложено напряжение, то заполняющее его вещество приобретает свойства одноосного кристалла. Линейно поляризованная световая волна в ячейке Керра распадается на две волны – обыкновенную и необыкновенную.
Плоскость колебаний вектора Ео обыкновенной волны совпадает с полем конденсатора, а вектора Ее необыкновенной волны – перпендикулярна полю. Из-за разной скорости распространения этих волн их фазы на выходе сдвигаются друг относительно друга. В результате из ячейки Керре выходит линейно поляризованная волна, которую можно исследовать с помощью компенсатора Бабине и анализатора П2. Опыт показывает, что величина оптической анизотропии Dn = ne – no пропорциональна квадрату напряженно-сти электрического поля в конденсаторе. Dn = ne – no = КЕ2. Закон Керра, 1815 (20.7)
Здесь К – постоянная Керра. Чем она больше, тем ярче выражен эффект.
В таблице 20.3 приведены значения постоянной Керра К для некоторых жидкостей при температуре 20оС и l =589 нм. Как видно из таблицы, эффект выражен довольно слабо. Например, в кювете с нитробензолом длиной l =0,1 м находится конденсатор, расстояние между пластинами которого 3 мм. К конденсатору приложено напряжение 2500 В. При этих условиях, разность хода D= l∙Dn=l∙K∙E2 = 0,1∙2,2∙10–18×(2500ç3∙10–3)2 = 153 нм. Если в работе используется луч лазера с l = 630 нм, то эта разность хода соответствует четверти длины волны. Ячейка Керра эквивалента в этом случае четвертьволновой пластинке.
| Таблица 20.3 | |
| Жидкость | К, м2/В2 |
| Нитробензол C6H5NO2 | 2.2×10–18 |
| Нитротолуол CH3-C6H- NO2 | 1.2×10–18 |
| Хлорбензол C6H5Cl | 1.0×10–19 |
| Вода H2O | 4.7×10–20 |
| Сероуглерод CS2 | 3.2×10–20 |
| Бензол С6H6 | 6.0×10–21 |
| Хлороформ CHCl3 | –3.5×10–21 |
Из всех исследованных чистых веществ нитробензол имеет самое большое значение постоянной Керра К. У других веществ оно значительно меньше.
Время релаксации ячейки Керра с низкомолекулярным веществом (например, нитробензолом) не превышает 10–11 секунды. Такой промежуток времени достаточен для того, чтобы через ячейку прошло большое число волновых цугов с периодом колебаний порядка 10–14 секунды, но очень мал по сравнению с используемыми в технике интервалами времени. Поэтому ячейка Керра широко используется в качестве практически безынерционного затвора для световых лучей, а также для модуляции светового потока.
Теоретически эффект Керра объяснили Поль Ланжевен в 1910 году и Макс Борн в 1916 году как следствие поляризации вещества в электрическом поле. Электрическое поле не только ориентирует молекулы, но и создает в них дипольный момент. В результате действия поля в веществе возникает определенная ориентация частиц и как следствие – оптическая анизотропия. Тепловое движение препятствует ориентации атомов и молекул, поэтому постоянная Керра убывает с ростом температуры.
8. Магнитооптический эффект состоит в возникновении оптической анизотропии в веществах, помещенных в магнитное поле. Впервые этот эффект наблюдал Джон Керр в коллоидных растворах в 1901 году. Подробно его исследовали в 1907-1910 годах Э. Коттон и А. Мутон, поэтому его часто называют эффектом Коттона–Мутона.
Эффект Коттона – Мутона наблюдается в веществах с анизотропными молекулами, обладающими постоянным и отличным от нуля магнитным моментом (парамагнетики). В магнитном поле молекулы парамагнетика ориентируются вдоль по силовым линиям поля. В результате вещество становится анизотропным, оптическая ось его направляется вдоль поля.
Схема наблюдения эффекта Коттона – Мутона такая же, как схема наблюдения эффекта Керра (рис.188) при условии, что магнитные силовые линии идут так же, как электрические. Анизотропия вещества в магнитооптическом эффекте так же, как и электрооптическом эффекте Керра пропорциональна квадрату поля. ne – no = СВ2. (20.8)
Здесь С – постоянная Коттона – Мутона.
Магнитооптический эффект невелик. У нитробензола, например, постоянная С = 6,6×10–9 Тл-2. В магнитном поле с индукцией 2 Тл на пути 10 см возникает разность хода D = l(ne–no) = l×C×B2 =0,1∙6,6∙10–9∙4 = 2,64 нм. Для желтой линии натрия l = 589 нм это составляет всего 2,64ç589 » 0,005×l. Поэтому для изучения этого эффекта нужны сильные магнитные поля.
Дата добавления: 2020-05-20; просмотров: 792;











