Дифракция в параллельных лучах

1. Виды дифракции.В оптике различают два типа дифракционных явлений. В тех случаях, когда дифракционная картина, создаваемая сферической или плоской волной, изучается в точке, лежащей на конечном расстоянии от препятствия, говорит о дифракции Френеля. Эти явления рассмотрены в § 13 и § 14.

Йозеф Фраунгофер изучил в 1820 г. типы дифракции в параллельных лучах. Дифракционная картина, образованная параллельными лучами, формируется в идеале на бесконечности от препятствия, а реально в фокусе собирающей линзы. В результате освещенность картины сильно увеличивается.

В отличие от дифракции в сходящихся лучах, называемой дифракцией Френеля, дифракцию в параллельных лучах называют дифракцией Фраунгофера. Последняя имеет важное значение в виду того, что на ее основе создан такой замечательный многолучевой интерферометр как дифракционная решетка.

2. Дифракция света на щели.Пусть на щель шириной а перпендикулярно падает пучок параллельных лучей (рис.126). Щель СВ вырезает часть падающей плоской волны. Все точки этой части фронта являются источниками вторичных когерентных волн, которые интерферируют друг с другом. Результат интерференции в любом направлении под углом j можно определить, если разбить щель на зоны так, чтобы каждые две вторичные волны были сдвинуты друг относительно друга на полволны, то есть lç2.

Если разбиение дает четное число зон, то все волны попарно гасят друг друга, и в направлении j наблюдается минимум освещенности. Если же разбиение дает нечетное число зон, то одна волна остается не скомпенсированной, и в направлении j наблюдается максимум освещенности.

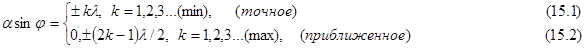
Для наблюдения дифракционной картины в параллельных лучах на конечном расстоянии используется собирающая линза, в фокальной плоскости которой размещается экран (рис.127). На экране наблюдаются светлые и темные полосы, параллельные щели. В центре, где j = 0, всегда наблюдается светлая полоса (центральный максимум).

Максимальное число темных полос в любую сторону от центра находится из условия: sinj = klça = 1. Отсюда k_max= açl.

Если ширина щели меньше l, нет ни одного минимума. Все пространство заполнено центральным максимумом.

С увеличением ширины щели положение первых минимумов смещается к центру картины, центральный максимум становится все резче. При a >> l в центре получается резкое изображение щели, а боковые максимумы становятся неразличимыми.

Обычная оптическая щель в лабораторных условиях имеет ширину не более 1 мм. Если ее длина в 50-100 раз больше ширины, щель может считаться одномерной.

Диаметр линзы, с помощью которой формируется дифракционная картина от щели, обычно в сотни и тысячи раз больше ширины щели. Если щель перемещать параллельно самой себе и экрану в пределах линзы, то дифракционная картина, наблюдаемая на экране, остается неподвижной. Ее главный максимум лежит в фокусе линзы.

Если расстояние от щели до экрана много больше ширины щели, то дифракция Фраунгофера будет реализоваться и в отсутствии линзы, при условии, что на щель падает плоская волна. В этом случае лучи, идущие от краев щели к любой точке экрана, остаются практически параллельными.

3. Дифракция света на круглом отверстии. Если длину щели уменьшить так, чтобы получилось прямоугольное отверстие со сторонами, мало отличающимися друг от друга, то дифракционная картина получается как бы от двух щелей, перпендикулярных друг другу (рис.128).

Если же отверстие круглое, то дифракционная картина получается в виде концентрических светлых и темных полос (рис.129). Во всех случаях в центре светлое пятно. Решение дифракционной задачи от круглого отверстия в параллельных лучах сложно, поскольку зоны Френеля имеют разную площадь. Поэтому длины суммируемых векторов в векторной диаграмме так же имеют разные значения.

Угловой радиус темных колец определяется приближенным соотношением: 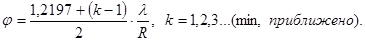(15.3)

Здесь R-радиус отверстия, k-номер темного дифракционного кольца, считая от центра.

Дифракция света на круглом отверстии очень важна в практике оптических приборов, поскольку все оправы линз и объективов имеют круглую форму.

В чистом виде эта дифракция реализуется в телескопах при наблюдении звезд. Поскольку звезды удалены от Земли на столь огромные расстояния, что их угловые размеры находятся за пределами оптического разрешения, свет от них идет параллельными лучами. При наблюдении звезды в фокусе телескопа получается не изображение звезды, а дифракционная картина от круглой оправы объектива телескопа в параллельных лучах.

Как видно из формулы (15.3), чем больше диаметр объектива 2R, тем меньше самое маленькое дифракционное кольцо, тем точнее можно определить положение звезды.

4. Дифракционная решетка– это система из большого числа параллельных щелей одинаковой ширины а, расположенных на одинаковом расстоянии друг от друга b. Расстояние a + b = d называется периодом решетки.

Если на решетку падает волновой фронт, то интерферируют не только вторичные волны, идущие от разных точек одной щели, но и волны, идущие от соответственных (одинаково расположенных) точек разных щелей (рис.130).

Закономерности интерференции вторичных волн на N щелях можно сформулировать в виде трех выводов.

а. Если решетка находится от линзы на расстоянии L >> Nd, где N – число щелей решетки, d – ее период, то интерференционные картины от одиночных щелей просто накладываются одна на другую. Интенсивность света в каждой точке интерференционной картины от одной щели в случае решетки увеличивалась в N раз.

На рис.127 условию L >> Nd соответствует перенос щели в пределах линзы. Независимо от положения щели все лучи, идущие под углом j, соберутся в точке A.

б. Появляются направления, в которых волны от соответственных точек щелей усиливают друг друга, dsinj = ± kl, где k = 0, 1, 2, 3 … . Это главные максимумы решетки. Центральному максимуму соответствует k = 0.

в. Появляются направления, в которых система лучей от всех N щелей дает нулевую освещенность, поскольку набегающая от всех N щелей в этих направлениях разность хода составляет целое число длин волн. (N∙d)sinj = ± kl, где …Векторная сумма амплитуд образует замкнутый многоугольник. Замыкающий вектор обращается в нуль. Этим направлениям соответствуют вторичные минимумы (первичными называют минимумы у одной щели). Их число N – 1. Итак, интерференционная картина от дифракционной решетки определяется тремя условиями:

аsinj = ± kl, k = 0, 1, 2, 3 … . (минимумы единичной щели) (15.4)

dsinj = ± kl, k = 0, 1, 2, 3 … . (главные максимумы решётки) (15.5)

(N∙d)sinj = ± kl, … (вторичные минимумы системы N щелей) (15.6)

На рис.131 показана схема расположения максимумов и минимумов интенсивности в интерференционной картине от решетки с параметрами: . По горизонтальной оси отложены значения sin 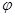в пределах от –1 до +1. Здесь: 1-кривая, показывающая расположение максимумов и минимумов в интерференционной картине от одной щели, 2-кривая интенсивности главных максимумов. Их число соответствует dçl = 4. (в одну сторону нуля). Но в направлениях, соответствующих sinj = ± ½ и sinj = ± 1, главне максимумы приходятся на минимумы одиночной щели. Там нет света, поэтому главные максимумы в направлениях k = ± 2 и k = ± 4 не реализуются.

5. Вторичные минимумы решетки.Рассмотрим их появление подробнее. В случае системы N щелей к минимумам, создаваемым каждой щелью порознь, добавляются минимумы, возникающие в результате интерференции элементарных волн, приходящих от соответственных точек всех N щелей. Разность хода, возникающая между крайними элементарными лучами решетки, идущими от соответственных точек в направлении угла j, равна D = Nd∙sinj. Здесь Nd – ширина решетки (рис.132).

Если эта разность хода кратна целому числу волн, то векторная сумма амплитуд световых векторов от этих волн образует замкнутый многоугольник. Замыкающий вектор равен нулю. Поэтому нулю равняется освещенность в этом направлении. Возникает вторичный минимум. Из уравнения Nd∙sinj = kl можно определить разность фаз Dj между элементарными волнами, идущими от соседних соответственных точек в направлении угла j. 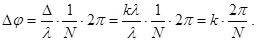(15.7)

На рис.133 показаны векторные диаграммы, соответствующие первому вторичному минимуму (k = 1) для решеток с одинаковыми периодами d и шириной щели а, но с разным числом щелей N. Все многоугольники замкнуты, замыкающий вектор равен нулю.

С ростом k форма векторных диаграмм меняется. На рис.134 показана эволюция векторной диаграммы решетки с N = 6 щелями с ростом k от 1 до 6. При k = 2 шестиугольник распадается на два одинаковых замкнутых треугольника. При k = 3 диаграмма представляет собой три пары одинаковых по модулю и противоположных по направлению векторов. При k = 4 шестиугольник распадается, как и при k = 2, на два одинаковых замкнутых треугольника. При k = 5, то есть k = N – 1 повторяется ситуация при k = 1. Итак, при k = 2 вся решетка как бы делится по длине на две части с одинаковыми комбинациями векторных диаграмм. При всех k от 1 до N – 1 имеют место вторичные минимумы.

Но ситуация меняется при k = N, в нашем примере при k = 6 (рис 135). Фазовый сдвиг между соседними элементарными волнами 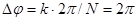. Все волны от соседних точек сдвинуты друг относительно друга на l, колеблются в одной фазе и поэтому усиливают друг друга. Это направление j соответствует первому главному максимуму решетки. .

Такая же ситуация имеет место при k = 2N, 3N и так далее. Из условия 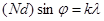, определяющего направление j вторичных минимумов, выпадают направления j, соответствующие k = 0, N, 2N… . Это направления главных максимумов решетки.

Между каждыми двумя главными максимумами дифракционной решетки помещается N – 1 вторичных минимумов. В направлениях главных максимумов амплитуды световых векторов складываются, так что при N щелях E = NE_i, где E_i – амплитудный световой вектор от одной щели. Отсюда следует, что интенсивность света в направлениях главных максимумов пропорциональна квадрату числа щелей решетки, .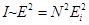

С другой стороны, чем больше число щелей N в решетке, тем теснее расположены вторичные минимумы между главными максимумами. Поэтому практически весь свет, проходящий через дифракционную решетку с N = 5000 ± 10000, локализуется в узких углах, соответствующих главным максимумам решетки.

6. Отражательная решетка представляет собой металлическую зеркальную пластину, на которой нанесена система параллельных штрихов с постоянным периодом.

Если q - угол падения лучей на решетку, y - угол дифракции, то разность хода двух соответственных лучей равна 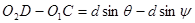(рис.136-а). Условие главных максимумов: (15.8)

Преобразуем по формулам тригонометрии: .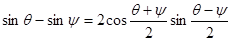

В случае грубых решеток, когда 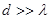, угол дифракции y мало отличается от угла падения q (по абсолютной величине), .

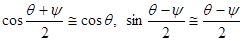Условие (15.8) принимает вид: d∙cosq sin(q –y) = ±kl (15.9)

Разность q –y = j есть угол дифракции, отсчитываемый от отраженного луча. Условие главных максимумов принимает в этом случае привычный вид (рис.136-б). 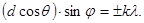(15.10)

Выражение d∙cosq есть проекция периода d на фронт волны. Чем больше угол падения q, тем меньше эффективный период решетки d∙cosq, тем больше ее дисперсия.

6. Разрешающая способность оптических приборов. В геометрической оптике полагается, что идеальная оптическая система преобразует один гомоцентрический пучок в другой. То есть лучи, вышедшие из светящейся точки, взаимодействуя с линзой, зеркалом, более сложной системой, снова сходятся в точку. Или в точку сходятся их продолжения. Говорят, каждой точке пространства предметов соответствует точка в пространстве изображений. Но свет – волновой процесс. Поэтому изображение предмета в оптической системе представляет собой дифракционную картину волн, идущих от предмета и взаимодействующих с оптической системой.

В телескопе с радиусом объектива R изображение святящейся точки (звезды на большом расстоянии) представляет собой не точку, а систему дифракционных концентрических колец. Угловой радиус первого темного кольца (его называют кругом Эйри) находится из формулы (15.3) при k = 1. j_min = 0,61lçR. (15.11)

Этот угол j_min и определяет предел углового разрешения телескопа. Если угол между направлениями на две звезды менее j_min = 0,61lçR, то их круги Эйри сливаются, и обе звезды воспринимаются как одна.

Применительно к микроскопу интерес представляет не угловое, а линейное разрешение, то есть то минимальное расстояние l_min, на котором две точки на предметном стекле микроскопа воспринимаются еще раздельно. , (15.12)

где n – показатель преломления среды, в которой находится рассматриваемый в микроскоп предмет, a – апертурный угол, то есть угол между оптической осью объектива и направлением от предмета на край объектива.

С целью уменьшения l_min предмет заливают иммерсией – прозрачной жидкостью с большим значением n. Апертурный угол обычных микрообъективов не более 10°. Используя иммерсию с n = 1,5, получаем в желтых лучах l_min = 0,61∙589∙10^–9ç1,5sin10°= 1,4 м = 1,4 мкм. На воздухе l_min = 1,4∙1,5 = 2 мкм.

Отрезок длиной l_min = 1.4 ¸ 2 мкм воспринимается под микроскопом еще как отрезок прямой и наблюдается при увеличении 300^´ ¸ 600^´. С уменьшением длины предмета его геометрия уже не воспринимается, наблюдается дифракционное пятно. Наращивание увеличения не спасает положение. Когда размер предмета станет менее l, дифракционное пятно исчезнет, предмет не наблюдается при любом увеличении.