Эллиптическая поляризация света

1. Интерференция линейно поляризованных волн. Все случаи интерференции, рассмотренные в главе 3, характерны тем, что соответственные элементы интерферирующих когерентных волн поляризованы в одной плоскости. Каждому цугу одной волны соответствует его двойник в другой, когерентной волне. Функции всех интерференционных приспособлений – бипризмы Френеля, билинзы Бийе и других – как раз и сводятся к тому, чтобы формировать вторичные цуги, во всем тождественные между собой. Наложение только таких волн приводит к интерференционному эффекту – перераспределению интенсивности света в пространстве.

При изучении поляризованного света возникает вопрос: как взаимодействуют между собой цуги, поляризованные во взаимно перпендикулярных плоскостях. Чтобы ответить на него, выясним характер поведения вектора напряженности суммарного электрического поля, возникающего при наложении двух когерентных линейно поляризованных волн с взаимно перпендикулярными плоскостями колебаний вектора .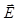

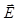Пусть вдоль оси ОХ распространяются две линейно поляризованные когерентные волны, плоскости колебаний векторов которых взаимно перпендикулярны. Например, вектор 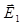колеблется вдоль оси OY, а 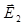- вдоль оси OZ (рис.164). Обе волны имеют между собой сдвиг по фазе на некоторый угол j.

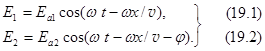
Электрическое поле подчиняется принципу суперпозиции. Поэтому вектор напряженности 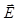суммарного электрического поля в любой момент времени и в любой точке пространства равен сумме векторов 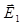и 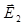. Пространство, в котором распространяются волны, полагаем изотропным. В этом случае фазовый сдвиг между волнами остается постоянным.

Найдем уравнение годографа вектора 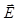суммарного поля в фиксированной точке пространства. Для упрощения уравнений удобнее всего взять точку х = 0.

Задача сводится к отысканию формы кривой, которую описывает конец вектора 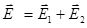в неподвижной плоскости, перпендикулярной оси ОХ и расположенной в точке х =0. Уравнение волн в этом случае упрощается.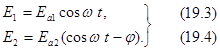

Исключим из уравнения время t. Для этого выразим из первого уравнения 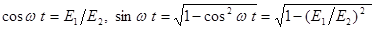. Распишем во втором уравнении косинус разности аргументов и подставим в него cosw t и sinw t из первого. 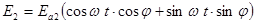. Получаем: 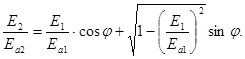(19.5)

Оставим корень в правой части и возведем уравнение в квадрат. После преобразований получаем: 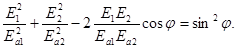(19.6)

Это уравнение эллипса. Конец вектора 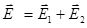описывает в фиксированной плоскости эллипс. Поэтому получающаяся волна называется эллиптически поляризованной.

Форма эллипса зависит от соотношения амплитуд напряженностей электрических полей складываемых волн E_a1 и E_a2, а так же от величины угла j фазового сдвига волн.

Рассмотрим несколько частных случаев.

а. Сдвиг по фазе отсутствует, j =0. Уравнение эллипса в этом случае вырождается в уравнение прямой. 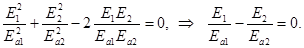(19.7)

Получается также линейно поляризованная волна, вектор 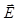которой колеблется в плоскости, ориентированной под углом a к плоскости колебаний вектора 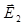(рис.165-а). Очевидно, tga =E_a1/E_a2. Годографом вектора 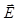является в этом случае прямая линия.

б. Сдвиг по фазе j = p/2. (Отставание на четверть волны). Уравнение эллипса при этом упрощается.

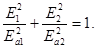(19.8)

Полуосями эллипса являются в этом случае амплитудные значения векторов напряженности E_a1 и E_a2 (рис.165-б). Если E_a1=E_a2 (интерферируют волны одинаковых интенсивностей), то эллипс вырждается в окружность. В этом случае говорят, волна поляризована по кругу или циркулярно поляризованная волна.

в. Сдвиг по фазе j = p. (отставание на полволны). Как и в первом случае, эллипс вырождается в прямую (рис.165-в). 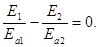(19.9)

Чтобы представить графический образ эллиптически поляризованной волны, нужно принять во внимание, что годограф вектора 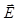в неподвижной плоскости есть траектория точки пересечения неподвижной плоскости с годографом 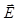движущейся волны. Поэтому пространственный годограф эллиптически поляризованной волны растягивается в эллиптическую пружину, годограф циркулярно поляризованной волны – в цилиндрическую пружину, а годограф линейно поляризованной волны – в плоскую синусоиду.

2. Получение эллиптически поляризованной волны можно реализовать с помощью плоскопараллельной пластинки, вырезанной из двоякопреломляющего кристалла (рис.166).

Если плоскость колебаний вектора E падающей на пластинку линейно поляризованной волны составляет с оптической осью кристалла АА угол a ¹ 0, то падающая волна расщепляется на две когерентные линейно поляризованные волны с взаимно перпендикулярными плоскостями колебаний вектора E. Обе волны распространяются в пластинке с разными скоростями.

При выходе из пластинки эти волны приобретают разность хода D = (n_е – n_o)∙d, где d – толщина пластинки, а n_е и n_o– показатель преломления пластинки по отношению к обыкновенному и необыкновенному лучам. Соответствующая этой разности хода D разность фаз j составляет j = (Dçl)∙2p.

Если D= lç2∙(j = p), говорят, пластинка в полволны. Этот случай рассмотрен в пункте 1-в (рис.165-в). Линейно поляризованная волна преобразуется также в линейно поляризованную волну с повернутой плоскостью поляризации.

Если D= lç4 (j = pç2), говорят пластинка в четверть волны. Этот случай рассмотрен в пункте 1-б (рис.165-б). Линейно поляризованная волна преобразуется в эллиптически поляризованную. Если угол a между плоскостью колебаний 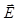падающей волны и оптической осью АА пластинки составляет 45°, то амплитудные векторы напряженности электрического поля обыкновенной E_a0 и необыкновенной E_ae волн одинаковы. (предполагается, что дихроизма нет). Получается частный случай эллиптической поляризации – циркулярно поляризованная волна.

3. Момент импульса циркулярно поляризованной волны. В 1898 году русский физик Александр Садовский теоретически предсказал, что на тело, облучаемое эллиптически или по кругу поляризованным светом, должен действовать вращающий момент. Это ожидаемое действие вращающего момента называют эффектом Садовского. Он обусловлен наличием у эллиптически поляризованной волны отличного от нуля момента импульса, который и передается волной телу, поглощающему ее или изменяющему состояние ее поляризации. Эффект Садовского очень мал. Экспериментально его удалось обнаружить лишь в 1935 году. Одиночный цуг циркулярно поляризованной электромагнитной волны (фотона) имеет момент импульса, равный постоянной Планка ћ = 1,05∙10^–34Дж∙с. Суть эффекта Садовского состоит в законе сохранения момента импульса.

Поскольку волна, эллиптически поляризованная, имеет отличный от нуля момент импульса, а линейно поляризованная не имеет его, то электромагнитный волновой цуг при прохождении через четверть волновую пластинку в любом случае изменяет свойства импульса. При прохождении слева направо по рисунку 166 линейно поляризованная волна «закручивается» и приобретает момент импульса. При прохождении справа налево в силу принципа обратимости эллиптически поляризованный цуг «выпрямляется» и теряет свой момент импульса. В обоих случаях четверть волновая пластинка получает равный по величине, но противоположный по направлению момент импульса отдачи.

4. Четверть волновая пластинка может быть изготовлена как из отрицательного так и положительного кристалла. Толщина ее d найдется из соотношения:

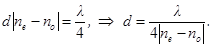(Здесь l – длина волны света в вакууме.) (19.10)

Толщина четвертьволновой пластинки, определяемая формулой (19.10), минимальна. Для пластинки исландского шпата при l = 555 нм она равна 0,8 мкм, для пластинки из кварца равна 15,4 мкм. Столь тонкие пластинки очень хрупки и неудобны в работе.

Обычно пластинки изготавливают большей толщиныlç4 + kl, где k = 1,2,3,… Тогда:

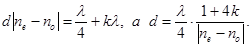(19.11)

Подбирая соответствующие значения k, можно изготовить достаточно толстую и прочную четвертьволновую пластинку. Направление закручивания волны определяется знаком разности n_е – n_o. Отрицательные и положительные кристаллы закручивают цуг в противоположных направлениях.

5. Изучение эллиптически поляризованного света. Трудность измерения параметров эллиптически поляризованного света состоит в том, что обычные поляризационные анализаторы, например, призма Николя, не позволяют отличать эллиптически поляризованный свет от частично поляризованного, циркулярно поляризованный – от естественного.

Если пропустить эллиптически поляризованный свет через николь, то при вращении николя вокруг оси луча (на рис.167 ПП – плоскость пропускания николя) наблюдаемый результат полностью совпадает с результатами пропускания частично поляризованного света. Интенсивность прошедшего через николь света в обоих случаях изменяется плавно, проходя через максимумы и минимумы.

Амплитуда прошедшего через анализатор света зависит от ориентации плоскости пропускания анализатора ПП относительно осей эллипса и определяется анализатором ОА.

При циркулярной поляризации эллипс превращается в окружность. Как бы не вращался николь вокруг оси луча, интенсивность падающего света будет оставаться постоянной. То же самое получается при прохождении естественного света.

Существуют три типа приборов для изучения эллиптически поляризованного света: четвертьволновая пластинка, компенсатор Бабине и компенсатор Солейля.

6. Изучение эллиптически поляризованного света с помощью четвертьволновой пластинки представляется наиболее эффективным. При определенной ориентации пластинки относительно осей эллипса свет эллиптически поляризованный превращается в линейно поляризованный, который уже может быть обнаружен анализатором (рис.168-а).

Естественный свет, состоящий из линейно поляризованных цугов, после четверть волновой пластинки превращается в статистике цугов в циркулярно – поляризованный (рис.168-б). Потому анализатор не выделяет в ней эффекта линейной поляризованности.

Однако использование четвертьволновой пластинки постоянной толщины имеет два недостатка.

а. Каждая пластинка является четвертьволновой лишь для определенной длины волны l. Для других длин волн она непригодна.

б. Чтобы эллиптически поляризованная волна, пройдя пластинку, превращалась в линейно поляризованную, нужно, чтобы оптическая ось пластинки совпадала с осью эллипса. Но для этого требуются дополнительные измерения.

Поэтому на практике для изучения эллиптически поляризованного света используются специально сконструированные приборы – компенсаторы Бабине и Солейля. (компенсаторы – в смысле компенсируют разность хода между компонентами Е_о и Е_е).

7. Компенсатор Бабине. В 1839 году француз Жак Бабине сделал устройство для изучения линейно поляризованного света, состоящее из двух слабо скошенных клиньев с взаимно перпендикулярными оптическими осями. Поэтому луч обыкновенный в первом клине становится необыкновенным во втором, и наоборот. Дополнительная разность хода между обоими лучами равна: 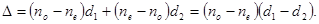(19.12)

Здесь d₁ и d₂ – геометрические пути прохождения луча в клиньях.

Если рассматривать поверхность компенсатора через николь в проходящем свете, то в зависимости от того, как поляризован свет, картина будет различной.

а. Компенсатор освещается естественным светом (рис.169). В этом случае в тех местах, где разность хода лучей D = lç4 (лучи 2,6,), а также D = 5lç4, 9lç4 и так далее, естественный свет превращается в циркулярно поляризованный (смотри рис.168-б). При любом угле поворота николя в этих местах наблюдается светлая полоса.

В тех местах, где D = 0, lç2, l, 3lç2, и так далее, образуется линейно поляризованный свет. Поэтому через половину оборота николя темная полоса в этих местах будет сменятся на светлую и наоборот (рис.170).

б. Компенсатор освещается циркулярно поляризованным светом. В этом случае в тех местах, где компенсатор соответствует четверть-волновой пластинке (D = lç4, 5lç4, 9lç4, … ), циркулярно поляризованная волна превращается в линейно поляризованную (смотри рис.168-а). При вращении николя в этих местах будут чередоваться светлые и темные полосы. В тех местах, где D = 0, lç2, l, 3lç2,…, характер линейно поляризованной волны не изменяется. Здесь наблюдается светлая полоса.

Бабине сконструировал свой компенсатор как окулярную насадку для поляризацион-ного микроскопа. Пластинка компенсатора может устанавливаться в этом случае в плоскости окулярной шкалы. Положение темных полос определяется просто по делениям шкалы.

8. Компенсатор Солейля. Для практической работы удобнее компенсаторы, вся поверхность зрения которых представляет область одной и той же добавочной фазы. Это реализуется в усовершенствованном варианте компенсатора Бабине – компенсаторе Солейля. Компенсатор Солейля состоит из двух клиньев и плоскопараллельной пластинки (рис.171). Оптические оси клиньев параллельны между собой и перпендикулярны оптической оси прямоугольной пластинки. Сдвигая или раздвигая клинья, можно установить любую нужную разность хода, которая одинакова по всему участку перекрытия клиньев.

9. Хроматическая поляризация. Так назвал группу явлений, связанных с эллиптической поляризацией света, Франсуа Араго в 1811 году. Он наблюдал слюдяные и гипсовые пластинки, освещенные линейно поляризованным светом, сквозь призму Рошона и обнаружил на поверхности этих кристаллов разноцветные полосы. Цвет этих полос изменяется в зависимости от того, в каком луче призмы Рошона велось наблюдение.

Схема для наблюдения хроматической поляризации включает в себя три основные элемента: поляризатор П1, формирующий пучок линейно поляризованных лучей, анизотропную пластинку Пл и поляризатор П2, играющий роль анализатора, через который ведется наблюдение (рис.172).

Если пластинка Пл создает в монохроматическом свете разность хода, кратную длине волны, D = l,2l, 3l,…, то при скрещенных поляризаторах (угол между плоскостями пропускания 90^о) наблюдается темнота, а при параллельных поляризаторах (параллельны плоскости пропускания) наблюдается свет. Если пластинка Пл создает разность хода, равному нечетному числу полуволн, D = lç2,3lç2, 5lç2,…, то при скрещенных поляризаторах виден свет, при параллельных – темнота.

Если пластинку Пл освещать линейно поляризованным белым светом, то оказывается, что всегда найдутся две волны l₁ и l₂, интерференционный максимум для одной из которых соответствует интерференционному минимуму для другой. Поэтому при скрещенных поляризаторах будет наблюдаться свет с длиной волны l₁, а при параллельных – с длиной волны l₂. Цвета, наблюдающиеся при параллельных и скрещенных поляризаторах, называются дополнительными. Соотношение между длинами волн l₁ и l₂ дополнительных цветов находится из системы уравнений:

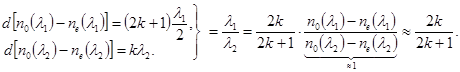(19.13)

Если анизотропная пластинка Пл имеет неравномерную толщину d или неодинаковый в разных точках коэффициент преломления, то разные точки такой пластинки будут создавать неодинаковую разность хода D. При освещении монохроматическим светом на ней будут видны светлые и темные полосы.

При освещении пластинки белым светом линии окрашены в разные цвета. При вращении поляризатора цвет линий постепенно меняется на дополнительный.