Дифракция в сходящихся лучах на щели

1. Зоны Шустера. Для изучения дифракции на одномерных препятствиях, таких как прямолинейный край полубесконечного экрана, щель и цилиндр, Артур Шустер предложил разбивать плоский волновой фронт не на кольцевые, а на полосатые зоны Френеля. Рассмотрим технологию определения светового вектора, возникающего при действии плоского бесконечного волнового фронта, с помощью полосатых зон (рис.115).

Пусть ФФ – бесконечная поверхность плоской волны, находящаяся на расстоянии L от расположенного параллельно волне экрана Э. Чтобы определить световой вектор действия светового фронта в точке А экрана, разобьем всю волновую поверхность на зоны Френеля, представляющие собой прямые полосы, перпендикулярные плоскости рисунка (зоны Шустера).

В отличие от кольцевых зон Френеля на поверхности сферы площадь плоскопараллельных зон неодинакова. Поэтому векторы Е от разных зон имеют разную длину, тем меньшую, чем дальше находится зона от точки О.

Поскольку зоны Френеля уходят в бесконечность вправо и влево, то это значит, что векторная диаграмма должна иметь две точки, к которым ассимптотически стремятся концы диаграммы (рис.116). В результате действие бесконечной волны ФФ в точке А представляется длиной вектора Е_¥, проведенного из одной ассимптотической точки В_¥' в другую В_¥. Впервые количественную дифракционную задачу о действии неограниченного волнового фронта решал Френель. Он разбивал волновой фронт на кольцевые зоны и получил решение в виде специальных интегралов (интегралов Френеля), которые находятся лишь численными методами.

Графически отобразил решение в виде центрально-симметричной спирали француз Мари Корню в 70-х г.г. 19 в. Поэтому диаграмму на рис.116 называют спиралью Корню. Участок АВ₁ на спирали Корню соответствует действию правой зоны 1 на рис.115, участок В₁В₂ - действию правой зоны 2 и так далее. Участки левой спирали соответствуют действию зон, расположенных слева от точки О.

2. Дифракция на краю прямолинейного полубесконечного экрана. Совмещаем плоский волновой фронт с плоскостью экрана и производим разбиение фронта на зоны Шустера, параллельные краю экрана.

Если точка А находится точно под краем препятствия, как показано на рис.117, то все левые зоны Френеля оказываются закрыты препятствием. Действие волнового фронта в точке А определится правой ветвью спирали Корню. Отсюда длина светового вектора Е в точке А равна половине длины вектора Е_¥ от бесконечного волнового фронта. 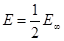. (14.1)

При смещении точки А вправо открывается столько полувитков левой спирали, сколько укладывается левых зон (рис.118).

А

При смещении точки А влево в область геометрической тени закрываются не только витки левой спирали Корню, но и часть полувитков правой спирали (на рис.119 - три), соответствующих числу закрытых правых зон.

Вычисленный так вектор Е позволяет найти распределение интенсивностей в дифракционной картине на краю полубесконечного экрана (рис.120). Здесь Е_¥, I_¥ - световой вектор и интенсивность, создаваемые в точке А неограниченным волновым фронтом.

3. Дифракция на щели. Если точка А находится под серединой щели, то освещенность в ней зависит от того, сколько зон Френеля укладывается на половине щели.

Если, как на рис.121, на каждой половине укладывается по одной зоне, то длина светового вектора Е, соединяющего на спирали Корню точки В₁' и В₁, максимальна. Максимальна и освещенность. Если на каждой половине щели укладывается по две зоны, то длина вектора Е, соединяющего точки В₂' и В₂ минимальна, в точке А относительно темно.

В целом можно сделать вывод: если на половине щели укладывается нечетное число зон, то на экране в центре щели свет. Если на половине щели укладывается четное число зон, то на экране в центре щели относительная темнота.

По мере увеличения ширины щели колебания интенсивности на экране под ее центром все менее заметны, а I ® I_¥.

Если точку А смещать к какому-либо краю щели, то в каждом конкретном случае величина светового вектора найдется по спирали Корню (рис.122).

4. Дифракция на длинном цилиндре. Пусть на пути светового пучка находится длинный непрозрачный цилиндр радиуса R. Форма сечения препятствия роли не играет. Это может быть узкая тонкая полоса, призма и так далее. Просто цилиндр легче реализуется на практике в виде волос, нитей, проволоки и других тел.

Волновой фронт как и в предыдущих случаях полагаем плоским. Разбиваем его на полосатые зоны и анализируем ситуацию.

В примере на рис.123 препятствие закрывает слева одну зону, а справа – две. Действие левой части волнового фронта выражается световым вектором , а действие правой части – световым вектором 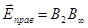. Суммарное действие в точке А определяется суммой этих векторов, .

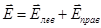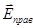Легко видеть, что если точка А находится в центре геометрической тени от препятствия, то количество закрытых зон слева и справа от точки О одинаково. Поэтому векторы и одинаковы по величине и одинаково ориентированы. Их сумма всегда отлична от нуля и больше, чем в точках А, смещенных вправо или влево в пределах 1 – 2 зон.

Это значит, что по центру геометрической тени от цилиндра всегда проходит светлая полоса, подобная светлому пятну Пуассона от круглого препятствия.

Заметим, что положение светлых и темных полос при дифракции света на цилиндре (рис.124-а) можно определить и не прибегая к спирали Корню.

Действие всего волнового фронта, как в случае шара или диска сводится к половине действия первой, ближайшей к цилиндру зоны. Но это значит, что вблизи геометрической тени задача сводится к интерференционной схеме Юнга: в точках М и N на концах диаметра цилиндра имеются два когерентных источника, излучающих в одной фазе (рис.124-б).

На экране должны наблюдаться светлые и темные полосы, параллельные оси цилиндра. В центре аналогично пятну Пуассона всегда будет светлая полоса. Наиболее контрастными являются темные полосы первого порядка (k = ± 1), между которыми находится центральная светлая полоса. Это объясняется тем, что разница в интенсивностях лучей от точек М и N здесь минимальна.

Из приближенного равенства Dç2R = YçL, где L – расстояние от цилиндра до точки наблюдения А, получаем условия и координаты максимумов и минимумов.

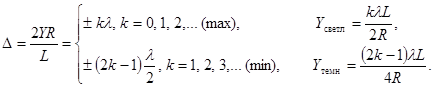
	(14.2)
(14.3)

Здесь D = l₂ – l₁ – разность хода между вторичными интерферирующими лучами.

5. Достоинства и недостатки метода зон Френеля. Достоинства – простота и наглядность. С его помощью, прибегая к относительно простым вычислениям, можно оценить как амплитуду, так и интенсивность световой волны в любой точке наблюдения.

Однако метод зон Френеля не позволяет построить последовательную точную теорию по нескольким причинам.

а. Метод Френеля, правильно определяя амплитуду результирующего колебания, неудачно определяет его фазу. Получается, что фаза колебания светового вектора Е в точке А, обусловленного всей сферической волной, отличается на pç2 от фазы колебаний центральной точки в центральной зоне (рис.125). Тогда как очевидно, что фаза колебаний светового вектора в точке А должна совпадать с фазой колебаний центральной точки центральной зоны, то есть Е_¥ должно быть в положении Е₀.

б. Формулировка Френеля в принципе Гюйгенса-Френеля содержит трудность, состоящую в том, что из нее следует наличие двух вторичных волн: одной, идущей вперед от источника света, и другой, построенной так же, как огибающая элементарных волн, но по направлению обратно к источнику.

в. Теория Френеля, разработанная в модели упругих волн, не учитывает взаимодействие света с веществом препятствия. Правда, это взаимодействие проявляется лишь на расстояниях, меньших длины волны. Поэтому на наблюдаемых дифракционных картинах оно практически незаметно.

В 1882 г. Густав Кирхгоф показал, что все поправки, за исключением последней, учитываются, если при решении дифракционных задач исходить из дифференциальных волновых уравнений оптики.

В 1894 г. Арнольд Зоммерфельд первый решил дифракционную задачу на краю идеально проводящего экрана в теории электромагнитных волн с учетом их взаимодействия с веществом экрана.