Дифракция Вульфа – Брэгга.
Вскоре после открытия М.Лауэ (1912) электромагнитной природы рентгеновских лучей русский ученый Ю.В. Вульф (1912) и независимо от него английские физики отец и сын Г. и Л.Брэгги дали простое истолкование интерференции рентгеновских лучей, объяснив это явление зеркальным отражением от атомных плоскостей.
Пусть на кристалл, который можно представить состоящим из семейства параллельных атомных плоскостей, находящихся на одинаковом межплоскостном расстоянии d (рис 2.2.1), под углом 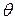 падает параллельный пучок монохроматических рентгеновских лучей с длиной волны
падает параллельный пучок монохроматических рентгеновских лучей с длиной волны 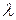 .
.

Отраженные от атомных плоскостей под тем же углом 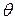 ( зеркальное отражение), параллельные лучи I и II интерферируют, т.е. усиливают или ослабляют друг друга в зависимости от разности хода между ними. Если разность хода
( зеркальное отражение), параллельные лучи I и II интерферируют, т.е. усиливают или ослабляют друг друга в зависимости от разности хода между ними. Если разность хода 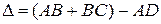 равна целому числу n длин волн
равна целому числу n длин волн 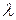 , то наблюдается интерференционный максимум. Из рис. 2.2.1 видно, что это имеет место, когда
, то наблюдается интерференционный максимум. Из рис. 2.2.1 видно, что это имеет место, когда
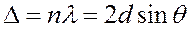 или
или 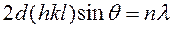 . (2.2.1)
. (2.2.1)
Условие (2.2.1), при котором возникает интерференционный максимум, и носит название формулы Вульфа – Брэгга. Зная брэгговские углы отражения 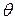 , которые определяются из дифракционной картины, можно вычислить межплоскостные расстояния d, а по ним и индексы интерференции hkl.
, которые определяются из дифракционной картины, можно вычислить межплоскостные расстояния d, а по ним и индексы интерференции hkl.
Условие дифракции в терминах обратной решетки.Рассмотрим обратную решетку и мысленно проведем атомную плоскость из семейства атомных плоскостей (hkl) c межплоскостным расстоянием d. Пусть на решетку падает излучение с волновым вектором 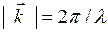 и выполняется условие дифракции Вульфа-Брэгга (2.2.1). Тогда из рис.2.2.1 и ранее доказанной теоремы,
и выполняется условие дифракции Вульфа-Брэгга (2.2.1). Тогда из рис.2.2.1 и ранее доказанной теоремы,  устанавливающей связь между семейством атомных плоскостей и вектором обратной решетки, можно записать следующую цепочку равенств:
устанавливающей связь между семейством атомных плоскостей и вектором обратной решетки, можно записать следующую цепочку равенств:
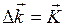
 где m – порядок дифракционного максимума. При m=1 условие дифракционного максимума принимает окончательный вид
где m – порядок дифракционного максимума. При m=1 условие дифракционного максимума принимает окончательный вид
(2.2.2)
Умножив обе части уравнения (2.2.2) на 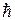 получим
получим
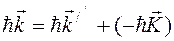

 (2.2.3)
(2.2.3)
Уравнение (2.2.3) можно рассматривать как закон сохранения импульса для кристаллической решетки.
Метод Лауэ.
Пусть на неподвижный кристалл (рис.2.3.1) падает пучок рентгеновского излучения, содержащего все длины волн – от 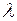 до некоторого
до некоторого  .
.
Для того чтобы понять характер и происхождение лауэграммы (рис.2.3.2), обратимся к трактовке интерференции с помощью обратной решетки и сферы Эвальда.
Если на кристалл падает спектр, содержащий длины волн от 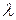 до
до  это означает, что имеется непрерывный ряд сфер Эвальда с радиусами от
это означает, что имеется непрерывный ряд сфер Эвальда с радиусами от 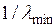 до
до 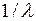 (рис.2.3.3).
(рис.2.3.3).

Все те узлы обратной решетки, которые попали в область между граничными сферами (на рис.2.3.3 заштрихованная область), находятся в отражающем положении, поскольку для них выполняется условие Вульфа – Брэгга. Как можно видеть из рис. 2.3.2 , в случае, если направление первичного пучка совпадает с одной из осей симметрии кристалла или лежит в плоскости симметрии, то такую же симметрию имеет и дифракционная картина, образованная лучами, которые испытали брэгговское отражение. Поэтому, ориентируя кристалл определенным образом относительно первичного пучка, всегда можно найти нужные направления, в частности направления, необходимые для выявления осей элементарной ячейки.

Дата добавления: 2021-02-19; просмотров: 770;











