Дифракция в сходящихся лучах
1. Дифракция света (от лат. diffractus – разламывание) – это явление, состоящее в загибании световых волн в область геометрической тени. Дифракцию открыл в 1650 г. экспериментально и назвал так итальянец Франческо Гримальди. Он же объяснил дифракцию света как результат проявления его волновой природы. Приближенную теорию дифракции разработал в 1818 г. Огюстен Френель. В основе ее лежит принцип Гюйгенса-Френеля. В электромагнитной теории света его можно сформулировать так:
Свет есть процесс распространения в пространстве генерируемых источником электромагнитных волн. Каждая точка фронта волны есть источник вторичных волн. Вторичные волны когерентны и поэтому интерферируют между собой.
2. Проблема прямолинейного распространения света – это первая проблема, которую пришлось решать в рамках волновой модели.
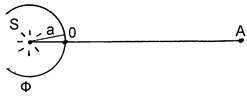 Рис.105 Рис.105
|
Пусть точечный источник S испускает монохроматическое излучение с длиной волны l. Волновой фронт Ф в однородной изотопной среде имеет в произвольный момент времени форму сферы радиуса а (рис.105).
Спрашивается, почему наблюдатель, находящийся вне волнового фронта в точке А, не воспринимает всю сферу как светящуюся поверхность? Ведь в точку А должны приходить все вторичные волны от всех видимых точек сферы.
3. Метод зон Френеля. Для подсчета суммарного действия вторичных волн в произвольной точке А Френель предложил разбивать волновой фронт на кольцевые зоны (рис.106). Граница первой зоны очерчивается лучом из точки А длиной L + lç2, внешняя граница второй зоны – лучом L + 2lç2, третьей зоны – лучом L + 3lç2 и так далее. Внешняя граница произвольной k-той зоны очерчивается лучом L + klç2.
 Если предположить, что поверхность волнового фронта Ф ламбертова, а зоны малы по сравнению с расстоянием до точки А, то можно считать, что интенсивность света от зон пропорциональна их площади. Найдем площадь зон.
Если предположить, что поверхность волнового фронта Ф ламбертова, а зоны малы по сравнению с расстоянием до точки А, то можно считать, что интенсивность света от зон пропорциональна их площади. Найдем площадь зон.
Шаровой сегмент высотой х и радиусом R, содержащий k зон имеет площадь 2pах, где а – радиус сферы. Величина х найдется из условия 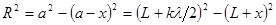 . Пренебрегая малыми членами l2 и х2, получаем
. Пренебрегая малыми членами l2 и х2, получаем  . Отсюда площадь k зон
. Отсюда площадь k зон 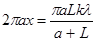 . (13.1)
. (13.1)
При увеличении числа зон на одну их суммарная площадь увеличивается на одну и ту же величину 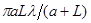 , равную площади центральной зоны. Но это значит, что площади всех зон одинаковы, а лучи, идущие от них в точку А, близки по интенсивности.
, равную площади центральной зоны. Но это значит, что площади всех зон одинаковы, а лучи, идущие от них в точку А, близки по интенсивности.
Интенсивность I электромагнитной волны пропорциональна квадрату амплитуды вектора напряженности Е0 электрического поля волны, I ~ Е02. Поэтому подсчет суммарной интенсивности сводится к сложению амплитудных векторов Е01, Е02, Е03 и так далее. Нечетные векторы направлены в одну сторону; а четные – в противоположную, поскольку волны от зон в точке А сдвинуты по фазе одна от другой на lç2. Это вытекает из условия построения зон.
С увеличением номера зоны проекция площади зоны, видимая из точки А, постепенно уменьшается. Уменьшается в точке А и модуль вектора Е0. Поэтому Френель предложил записать сумму так:  . (13.2)
. (13.2)
При постепенном убывании Е0 суммы в скобках стремятся к нулю. Поэтому  .
.
Действие всей волны в точке А сводится к половине действия центральной зоны. Вторичные волны от других участков волнового фронта, интерферируя, гасят друг друга. Радиус центральной зоны  очень мал. Так, при L @ a @ 10 м, R1 = 2 мм.
очень мал. Так, при L @ a @ 10 м, R1 = 2 мм.
Распространение света от S к А происходит так, как если бы световой поток шел внутри очень узкого прямого канала вдоль оси SA. Этот вывод и есть объяснение прямолинейного распространения света в волновой теории.
4. Зонная пластинка. Если изготовить такую пластинку, на которой нанесены концентрические круговые полосы, закрывающие четные или нечетные зоны Френеля, то лучи от открытых зон будут усиливать друг друга. В результате такой экран, называемый зонной пластинкой (Соре, 1875), увеличивает освещенность в точке А, действуя подобно собирающей линзе.
Зонные пластинки можно изготовить, сфотографировав интерференционную картину колец Ньютона в отраженных (рис.107-а) или в проходящих лучах (рис.107-б).
 Зонные пластинки в отличие от линз дают не одно, а несколько изображений источника S. Приближаясь к пластинке, мы придем в такую точку А, относительно которой в каждом прозрачном кольце пластинки будет укладываться не одна, а 3 зоны Френеля. Действие двух из них взаимно компенсируется, поэтому амплитуда колебаний вектора Е в точке А определяется лишь третьей зоной. Продолжая приближаться к пластинке, мы придем в точку А, для которой в каждом прозрачном кольце уложится 5 зон, и так далее.
Зонные пластинки в отличие от линз дают не одно, а несколько изображений источника S. Приближаясь к пластинке, мы придем в такую точку А, относительно которой в каждом прозрачном кольце пластинки будет укладываться не одна, а 3 зоны Френеля. Действие двух из них взаимно компенсируется, поэтому амплитуда колебаний вектора Е в точке А определяется лишь третьей зоной. Продолжая приближаться к пластинке, мы придем в точку А, для которой в каждом прозрачном кольце уложится 5 зон, и так далее.
Если на зонную пластинку падает плоский волновой фронт, то точки на оси пластинки с повышенной интенсивностью света можно интерпретировать как фокусы пластинки. Если f0 – расстояние от пластинки до ее главного фокуса, то есть до той точки А0, относительно которой зоны Френеля совпадают с зонами пластинки, то расстояние до фокусов, расположенных ближе к пластинке, определяются формулой: fk = f0ç(2k+1). (13.3)
 При удалении от главного фокуса А0 в сторону от пластинки площади зон Френеля увеличиваются. В результате могут возникать ситуации, когда центральная зона Френеля закроет 2 светлых и 1 темное кольцо пластины. В результате на оси также появляются слабые фокусы (рис.108).
При удалении от главного фокуса А0 в сторону от пластинки площади зон Френеля увеличиваются. В результате могут возникать ситуации, когда центральная зона Френеля закроет 2 светлых и 1 темное кольцо пластины. В результате на оси также появляются слабые фокусы (рис.108).
Самый дальний фокус находится в точке, из которой вся пластинка закрывается центральной зоной. Дальше интенсивность света непрерывно убывает по закону удаления от точечного источника.
Роберт Вуд изготовил пластинку, в которой непрозрачные кольца заменил также прозрачными, но так, что оптическая длина четных зон отличается от оптической длины нечётных зон на l/2. Поэтому свет от четных зон приходит в той же фазе, что и от нечетных. Такая пластина собирает весь падающий на нее свет.
Пластинка Соре создает повышенную интенсивность в фокусах А0, А1… путем деления волнового фронта. Пластинка Вуда кроме деления волнового фронта создает еще и сдвиг по фазе у четных или нечетных вторичных волн. Поэтому пластинку Вуда называют часто фазовой зонной пластинкой.
5. Дифракция на круглом отверстии.Пусть в непрозрачной стенке есть круглое отверстие радиуса R. На оси отверстия слева находится точечный источник S, излучающий монохроматический свет с длиной волны l (рис.109). Часть световых волн проходит сквозь отверстие и распространяется вдоль оси ОХ. Спрашивается, что должно наблюдаться – свет или темнота в точке А, расположенной на оси отверстия в сторону от источника S.
Для ответа на этот вопрос достаточно определить, четное или нечетное число зон укладывается на фронте волны Ф в пределах отверстия. При четном числе зон в точке А – темнота, при нечетном – свет.
6.  Распределение интенсивности света вдоль оси ОХ. Из геометрии рисунка 109 следует:
Распределение интенсивности света вдоль оси ОХ. Из геометрии рисунка 109 следует: 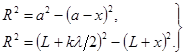
Пренебрегая членами, содержащими квадраты малых величин х и l, исключив х и разрешив систему относительно L, находим положение точки А, из которой на отверстии укладывается k зон Френеля.  .(13.4)
.(13.4)
 |
Так как L – положительное число, то знаменатель должен быть также положительным. Это условие накладывает ограничение на близость источника света к отверстию. Чтобы было возможно наблюдать первый дифракционный минимум, соответствующий k = 2, должно быть
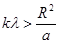 , или
, или  . Например для отверстия радиусом R = 1 мм и l = 550 нм аk=2 = 90 см.
. Например для отверстия радиусом R = 1 мм и l = 550 нм аk=2 = 90 см.
На рис.110 показано относительное изменение интенсивности света в точках на оси отверстия радиуса R = 0,5 мм при l = 550 нм и а = 1 м.
 Как видно из рисунка, чем дальше точка А от отверстия, тем меньше зон укладывается на нем, тем контрастнее наблюдаются темные (четные k) или светлые (нечетные k) точки. С приближением к отверстию уменьшаются не только расстояния между точками, но и глубина модуляции интенсивности света в них. Поэтому, чем ближе к отверстию, тем труднее эти точки наблюдать. Несмотря на некоторую нестрогость, при малых k метод зон Френеля является достаточно простым и надежным. С увеличением числа зон k на отверстии дифракционные кольца сжимаются к периферии и исчезают. В этом случае действуют законы геометрической оптики.
Как видно из рисунка, чем дальше точка А от отверстия, тем меньше зон укладывается на нем, тем контрастнее наблюдаются темные (четные k) или светлые (нечетные k) точки. С приближением к отверстию уменьшаются не только расстояния между точками, но и глубина модуляции интенсивности света в них. Поэтому, чем ближе к отверстию, тем труднее эти точки наблюдать. Несмотря на некоторую нестрогость, при малых k метод зон Френеля является достаточно простым и надежным. С увеличением числа зон k на отверстии дифракционные кольца сжимаются к периферии и исчезают. В этом случае действуют законы геометрической оптики.
7. Дифракция на круглом диске. Пусть между точечным источником S и точкой наблюдения А находится круглый диск радиуса R, геометрическая ось которого совпадает с осью SА (рис.111).
Вопрос: что должно наблюдаться в точке А – свет или темнота?
Задача решается на основе гипотезы Френеля: часть световой волны, прикрытая диском, не действует, как если бы ее не было. Неприкрытая часть волны действует так, как если бы не было диска.
Отсюда следует, что разбиение фронта волны на кольцевые зоны нужно начинать от края диска. В точке А должно наблюдаться половинное действие первой, ближайщей к диску зоны. Поэтому в центре геометрической тени диска в точке А всегда должно наблюдаться светлое пятно. К такому выводу пришел в 1818 г. Симеон Пуассон. Экспериментально светлое пятно Пуассона было обнаружено тогда же в опытах Франсуа Араго.
Приближая точку А к диску, можно по исчезновению светлого пятна Пуассона измерить максимальный угол g загибания света в область геометрической тени.
8. Графическое сложение амплитуд.Для того, чтобы изобразить графически действие целой зоны, нужно разбить ее на равные участки, столь малые, чтобы фаза колебаний вектора Е в точке А от разных элементов такого участка могла считаться постоянной. Действие всего участка в этом случае можно выразить вектором, длина которого дает суммарную амплитуду, а направление определяет фазу, обусловленную этим участком.
Вторичные волны, приходящие от разных краев зоны, сдвинуты по условию разбиения друг относительно друга на lç2, или, в угловой мере на p.
Для центральной зоны такими противофазными точками являются центр О и края зоны. Разобьем центральную зону на 8 равных участков (рис.112).
 Каждый суммируемый вектор повернут относительно предыдущего на угол j = pç8 = 22,5°. По длине эти векторы 1, 2, 3,… 8 практически не отли-чаются друг от друга, т. как обусловлены равновеликими участками фронта волны.
Каждый суммируемый вектор повернут относительно предыдущего на угол j = pç8 = 22,5°. По длине эти векторы 1, 2, 3,… 8 практически не отли-чаются друг от друга, т. как обусловлены равновеликими участками фронта волны.
 Таким образом, действие первой (центральной) зоны представляется вектором АВ1, который является суммой восьми векторов 1, 2, 3,… 8. Если разбить зону на бесконечно большое число бесконечно малых участков, то ломаная линия превращается в кривую, которая очень мало отличается от полуокружности.
Таким образом, действие первой (центральной) зоны представляется вектором АВ1, который является суммой восьми векторов 1, 2, 3,… 8. Если разбить зону на бесконечно большое число бесконечно малых участков, то ломаная линия превращается в кривую, которая очень мало отличается от полуокружности.
Чтобы учесть действие второй зоны, надо продолжить векторную диаграмму. Тогда мы получим вторую дугу, хорда которой В1В2 чуть меньше, чем у дуги АВ1 вследствие возрастающего наклона зоны (рис.113-а).
 Продолжая построение, получим диаграмму действия всей волны (рис.113-б). Действие всего волнового фронта выражается вектором АВ¥, который примерно в 2 раза меньше вектора АВ1, представляющее действие центральной зоны.
Продолжая построение, получим диаграмму действия всей волны (рис.113-б). Действие всего волнового фронта выражается вектором АВ¥, который примерно в 2 раза меньше вектора АВ1, представляющее действие центральной зоны.
При наблюдении дифракции от круглого отверстия поступаем так же. Величина светового вектора Е в произвольной точке А определяется вектором АВ, длина которого зависит от числа зон, уместившихся на отверстии (рис.114).
С увеличением размеров отверстия число зон увеличивается, световой вектор АВ колеблется по мере увеличения числа зон k с уменьшающейся амплитудой, приближаясь постепенно к АВ¥ невозмущенной волны.
Дата добавления: 2020-05-20; просмотров: 737;











