Интерференция в тонких пленках
1. Падение света на тонкую пленку. Пусть на поверхность прозрачной плоскопараллельной пластинки в точку О падает луч света (рис.91).
 Часть энергии падающего луча отражается в точке падения (луч 1), часть проходит в пластину и, отразившись от ее грани, выходит в точке В (луч 2). Часть энергии проходит сквозь пластину (луч 3) и часть поглощается. Рассмотрим лучи 1 и 2, отразившиеся от пластинки в точках О и В.
Часть энергии падающего луча отражается в точке падения (луч 1), часть проходит в пластину и, отразившись от ее грани, выходит в точке В (луч 2). Часть энергии проходит сквозь пластину (луч 3) и часть поглощается. Рассмотрим лучи 1 и 2, отразившиеся от пластинки в точках О и В.
Оба луча 1 и 2 параллельны, когерентны (получены расщеплением падающего луча) и мало отличаются по интенсивности.
Действительно, пусть коэффициент отражения света от границы раздела сред составляет 0,05 (5%). Полагаем, что интенсивность падающего в точку О луча равна I0. Тогда интенсивность отраженного в точке О луча 1 равна I1 = 0,05I0. Интенсивность прошедшего в пластину луча равна0,95I0. Пластинка тонкая и прозрачная, поэтому поглощением света в ней пренебрегаем. Интенсивность отраженного в точке С луча равна 0,05∙0,95I0, а интенсивность луча 2 I0 = 0,95(0,05∙0,95I0) = 0,045I0. Отсюда разница в интенсивностях лучей 1 и 2 не превышает 10%.
Вычислим разность хода лучей 1 и 2. Падающий луч расщепляется в точке О. Луч 1 сразу отражается, а луч 2 проходит внутрь пластинки. Наложение лучей происходит по прямой ЕВ. Луч 1 до наложения проходит отрезок ОЕ, а луч 2 – отрезок ОС + СВ. Но поскольку в средах с n > 1 длина волны l уменьшается в n раз, следует брать не геометрический, а оптический путь n(ОС + СВ).
Кроме того, как установил Т. Юнг, при отражении от оптически более плотной среды свет теряет полволны, то есть луч как бы проходит дополнительный путь lç2. В результате полная разность хода D между лучами 1 и 2 равна: 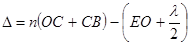 . (11.1)
. (11.1)
Если а –толщина пластинки, то из геометрии рисунка получаем:
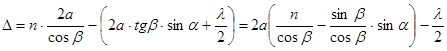 . (11.2)
. (11.2)
Упростим выражение, исключив b. Так как sina çsinb = n, 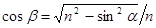 . Преобразовав выражение (11.2), запишем условия максимума и минимума.
. Преобразовав выражение (11.2), запишем условия максимума и минимума.
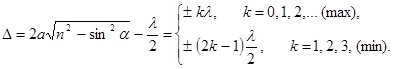
| (11.3) |
| (11.4) |
Число k называется здесь порядком интерференционного максимума (минимума). Оно тем больше, чем толще пластина.
Если смотреть на тонкую освещенную пленку, то при разности хода D, не выходящей за пределы длины когерентности света, можно увидеть на ее поверхности темные и светлые полосы. Различают полосы равной толщины и полосы равного наклона.
2. Полосы равного наклона. В формулу разности хода D входят два независимых параметра, которые могут изменяться. Это толщина пластины а и угол падения света a.
Рассмотрим здесь роль угла a.
 Если плоскопараллельную пластину освещать рассеянным монохроматическим светом, то, расположив параллельно пластине собирающую линзу, из всех рассеянных лучей самых разных направлений можно выделить параллельные лучи, которые собираются в фокусе линзы (рис.92).
Если плоскопараллельную пластину освещать рассеянным монохроматическим светом, то, расположив параллельно пластине собирающую линзу, из всех рассеянных лучей самых разных направлений можно выделить параллельные лучи, которые собираются в фокусе линзы (рис.92).
На экране, параллельном пластине и расположенном в фокальной плоскости линзы, будут видны чередующиеся светлые и темные кольца с центром на оптической оси линзы. Каждая полоса образована лучами, падающими на пластину под одним углом a. Такая интерференционная картина называется полосами равного наклона.
Поскольку полосы равного наклона наблюдаются в параллельных лучах, то говорят, что линии равного наклона локализованы в бесконечности. Их можно наблюдать и невооруженным глазом, роль линзы играет в этом случае хрусталик, а роль экрана – сетчатка.
3. Полосы равной толщины. Если наблюдать интерференцию в параллельных лучах, для которых a одинаково, то светлые и темные полосы будут соответствовать участкам пластины с одинаковой толщиной а. Такую интерференционную картину называют полосами равной толщины. Типичные примеры – интерференция на клине и кольца Ньютона.
а. Интерференция на клине. Если пластинка имеет форму клина с углом при вершине e, то лучи 1 и 2, отражающиеся от пластинки, в этом случае не параллельны и пересекаются на некотором расстоянии от клина (рис.93).
При освещении клина пучком параллельных лучей точки А1, А2,…, в которых сходятся когерентные лучи, лежат в одной плоскости ОА, проходящей через вершинное ребро клина.
 Чем острее клин, тем шире интерференционные полосы и тем дальше друг от друга они расположены. Если расстояние между полосами l, то между любыми соседними полосами набегает за счет изменения толщины разность хорда в одну длину волны, D=2l×tge×n=l, Þ
Чем острее клин, тем шире интерференционные полосы и тем дальше друг от друга они расположены. Если расстояние между полосами l, то между любыми соседними полосами набегает за счет изменения толщины разность хорда в одну длину волны, D=2l×tge×n=l, Þ
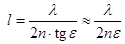 . (11.5)
. (11.5)
б. Кольца Ньютона – это интерференционная картина в виде системы концентрических светлых и темных колец. Наблюдается при нормальном освещении плосковыпуклой сферической линзы, помещенной выпуклой стороной на плоскую стеклянную пластину (рис.94-а). Впервые описана И. Ньютоном в 1675 г.
Интерференция света происходит благодаря тонкому воздушному зазору между нижней поверхностью линзы и верхней поверхностью пластинки.
Падающий сверху луч света на нижней поверхности линзы в точке М расщепляется. Часть луча отражается и идет вверх, другая часть проходит вниз, отражается от пластинки в точке N и также идет вверх. Выше точки М эти лучи накладываются друг на друга.
Оптическая разность хода лучей D = 2dn – lç2, где d – ширина воздушного зазора, n – показатель преломления воздуха. В данном случае можно полагать n = 1. Член l/2 появляется в результате потери фазы (запаздывания) на p при отражении света от оптически более плотного слоя в оптически менее плотный (от стекла в воздух в точке N).
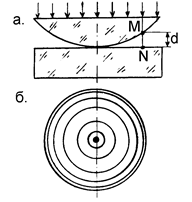 Рис.94 Рис.94
|
Там, где оптическая разность хода равняется целому числу длин волн, в отраженных лучах наблюдается свет. А там, где оптическая разность хода равняется нечетному числу полуволн, наблюдается темнота.
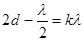 , максимум,
, максимум, 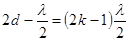 , минимум.(11.6)
, минимум.(11.6)
Поскольку области одинаковых значений d располагаются по окружности вокруг центра линзы, то интерференционная картина представляет собой множество концентрических темных и светлых колец (рис.94-б). Кольца Ньютона есть интерференционные линии равной толщины.
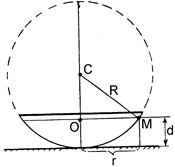 Рис.95 Рис.95
|
Связь между радиусом колец r и радиусом линзы R находится из рис.95. Из треугольника ОСМ следует, что r2 = R2 – (R – d)2 = 2Rd – d 2. Обычно радиус кривизны линз R не менее десятка сантиметров, тогда как зазор d не превышает десятка микрометров. Поэтому величина d 2 по крайней мере на 3 порядка меньше величины 2Rd. Это позволяет величиной d 2 пренебречь, r2 = 2Rd.
Выразив d из условий максимума и минимума, можно найти радиусы интерференционных колец Ньютона:
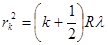 , светлые,
, светлые, 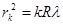 , темные. (11.7)
, темные. (11.7)
Здесь k = 1, 2, 3… - номер кольца, считая от центра. Центральному темному пятну соответствует k = 0.
Радиус линзы R и радиусы интерференционных колец r могут быть измерены достаточно просто традиционными методами. Поэтому интерференционные кольца Ньютона дают важную принципиальную возможность определить длину световых волн l.
4.  Метод наблюдения интерференции Поля. Немец Роберт Поль предложил метод наблюдения интерференции с большой светосилой. Свет от ртутной лампы отражается от плоскопараллельной тонкой пластинки (а » 0,04 мм, обычно слюда) на потолок аудитории. Поскольку высота потолка h много больше толщины пластины а, то угол g между мнимыми источниками света S1 и S2 оказывается малым (рис.96). Благодаря этому условие контрастности интерференционной картины оказывается мало чувствительным к размерам источника S.
Метод наблюдения интерференции Поля. Немец Роберт Поль предложил метод наблюдения интерференции с большой светосилой. Свет от ртутной лампы отражается от плоскопараллельной тонкой пластинки (а » 0,04 мм, обычно слюда) на потолок аудитории. Поскольку высота потолка h много больше толщины пластины а, то угол g между мнимыми источниками света S1 и S2 оказывается малым (рис.96). Благодаря этому условие контрастности интерференционной картины оказывается мало чувствительным к размерам источника S.
5. Просветление оптики. Если на поверхность стеклянной пластинки с показателем преломления n2нанести тонкую пленку с показателем преломления n < n2, то, подобрав толщину пленки а так, чтобы в отраженных лучах наблюдался интерференционный минимум, получаем оптическую систему с увеличенным коэффициентом пропускания.
 Условие минимума для отраженных нормально падающих лучей принимает вид (рис.97):
Условие минимума для отраженных нормально падающих лучей принимает вид (рис.97): 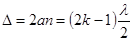 . (11.8)
. (11.8)
Поскольку обе волны 1 и 2 при отражении теряют по полволны, то член lç2 в левой части формулы 11.4 исчезает.
Толщина просветляющей пленки 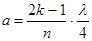 . (11.9)
. (11.9)
Обычно наносят предельно тонкую пленку, соответствующую k = 1. Тогда 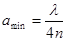 . (11.10)
. (11.10)
Наиболее полное гашение происходит при 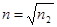 . Просветление рассчитывается обычно для желто-зеленой области спектра.
. Просветление рассчитывается обычно для желто-зеленой области спектра.
Найдем аmin для стекла с n2 = 1,5 и для l = 500 нм. Коэффициент преломления пленки 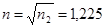 . Тогда аmin = (2k – 1)l ç4n = 500×10–9ç4×1,225 » 10–7 м = 0,1 мкм.
. Тогда аmin = (2k – 1)l ç4n = 500×10–9ç4×1,225 » 10–7 м = 0,1 мкм.
В настоящее время просветляющие пленки наносят на все линзы и призмы оптических систем. Один из технологических приемов просветления состоит в том, что стеклянную линзу (призму) опускают в кислотную ванну на некоторое время. Атомы тяжелых металлов из поверхностного слоя извлекаются, остается в основном оксид кремния SiO2, показатель преломления которого меньше, чем у стекла.
6.  Двухлучевые интерферометры.Это измери-тельные приборы, в которых используется интерференция двух световых волн. Наиболее широко используются приборы Жамена, Рэлея, Майкельсона.
Двухлучевые интерферометры.Это измери-тельные приборы, в которых используется интерференция двух световых волн. Наиболее широко используются приборы Жамена, Рэлея, Майкельсона.
а. Интерферометр Ж. Жамена, 1856 г. Состоит из двух толстых плоскопараллельных пластинок высокооднородного стекла, смонтированных на массивной плите почти параллельно друг другу (рис.98). Падающий на одну из пластин луч после отражения и преломления дает два параллельных когерентных луча 1 и 2. После отражения и преломления на второй пластине они дают 4 луча 11, 12, 21, 22. Лучи 11 и 22 пространственно далеки друг от друга и выводятся из оптической системы, а лучи 12 и 21 налагаются друг на друга и интерферируют между собой. Интерференционная картина наблюдается в зрительную трубу Т, сфокусированную на бесконечность.
Если между пластинами отличный от нуля угол, то при 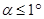 в трубу наблюдаются широкие полосы равной толщины. Если на пути одного из лучей 1 или 2 поместить прозрачную пластину или кювету с жидкостью или газом, то возникающая разность хода приводит к смещению интерференционных полос, которое может быть измерено. Это позволяет определять показатель преломления вещества.
в трубу наблюдаются широкие полосы равной толщины. Если на пути одного из лучей 1 или 2 поместить прозрачную пластину или кювету с жидкостью или газом, то возникающая разность хода приводит к смещению интерференционных полос, которое может быть измерено. Это позволяет определять показатель преломления вещества.
Построенные на базе интерферометра Жамена интерференционные рефрактометры используются для измерения показателей преломления газов, жидкостей, для измерения концентрации растворов.
 |
б. Интерферометр Дж. Релея. Сконструирован в конце 19 века и используется в основном как рефрактометр. Взаимодействующие пучки выделяются с помощью двух щелевых диафрагм (рис.99). Пройдя кюветы К1 и К2, эти пучки собираются в фокальной плоскости линзы Л2, где образуется интерференционная картина полос равного наклона, рассматриваемая через окуляр Ок.
Интерференционные рефрактометры относятся к числу наиболее чувствительных и точных приборов для измерения показателя преломления газов.
 в. Интерферометр А. Майкельсона, 1881 г. Сконструированный с целью определения влияния движения Земли на скорость света, он сыграл выдающуюся роль в истории науки. Прибор построен на основе двух плоских зеркал и двух стеклянных пластинок (рис.100).
в. Интерферометр А. Майкельсона, 1881 г. Сконструированный с целью определения влияния движения Земли на скорость света, он сыграл выдающуюся роль в истории науки. Прибор построен на основе двух плоских зеркал и двух стеклянных пластинок (рис.100).
Луч света от источника S падает на полупрозрачную пластинку Пл1, покрытую тонким слоем серебра или алюминия. В точке О луч расщепляется. Луч 1 сквозь прозрачную пластинку Пл2 идет на неподвижное зеркало Зк1. Отразившись от него в точке В, он возвращается к пластине Пл1 и, отразившись от нее в точке О, попадает в зрительную трубу Т.
Луч 2 идет на зеркало Зк2 и, отразившись от него в точке С, через пластину Пл1 также попадает в трубу Т.
Луч 2 дважды проходит сквозь пластину Пл1. Чтобы скомпенсировать возникающую за счет этого дополнительную разность хода, на пути луча 1 помещается точно такая же пластинка Пл2.
Если плечи интерферометра одинаковы, то лучи 1 и 2 имеют одинаковую интенсивность, когерентны и приходят в зрительную трубу с нулевой разностью хода.
Если зеркала Зк1 и Зк2 строго перпендикулярны друг другу, то в зрительную трубу Т, сфокусированную на бесконечность, видны темные и светлые кольца – полосы равного наклона. Если одно из зеркал, например Зк2, слегка наклонить, то в трубу наблюдаются темные и светлые полосы, параллельные ребру образовавшегося клина – полосы равной толщины.
При перемещении одного из зеркал, например Зк2, интерференционные полосы перемещаются. Поэтому, измеряя смещение полос, можно с очень высокой точностью измерить отрезки длин.
В 1892-93 г.г. с помощью сконструированного им интерферометра Майкельсон провел измерения длин волн спектральных линий разных элементов. В качестве эталона длины он предложил взять длину волны красной линии кадмия. С помощью девяти вспомогательных эталонов он сравнил эталон метра с длиной волны l. Первый эталон имел длину 0,39 мм, а каждый последующий примерно в два раза длиннее предыдущего. Последний эталон имел длину 100 мм.
В начале определялось число длин волн l, укладывающихся на длине первого эталона, а затем проводилось сравнение эталонов. Майкельсон получил, что 1 м » 1 553 163, 5 l.
Советский ученый В. Линник в 30-х годах 20 в. предложил заменить одно из зеркал в интерферометре Майкельсона металлической деталью, у которой должно быть проверено качество шлифовки поверхности. Глубина микронеровностей определяется в этом случае по величине провалов в системе интерференционных полос.
Дата добавления: 2020-05-20; просмотров: 640;











