Сложение световых волн
1. Сложение однонаправленных волн.Пусть на оси ОХ находятся два источника S1 и S2 в точках с координатами х1 и х2 (рис.81). В момент времени t = 0 источники начали излучать две монохроматические одинаковой частоты w линейно поляризованные в одной плоскости световые волны.

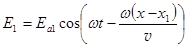 , (10.1)
, (10.1)
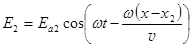 , (10.2)
, (10.2)
Здесь v - скорость распростране-ния волны.
Электрическое и магнитное поля подчиняются принципу суперпозиции. Поэтому при наложении волн в любой точке А их напряженности складываются. 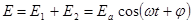 . (10.3)
. (10.3)
Здесь j = w(х2 – х1)/v - сдвиг фаз между волнами. Помимо параметров волны w и v на него влияет расстояние между источниками D = х2 – х1.
Сдвиг фаз определяет амплитуду Еасуммарной волны 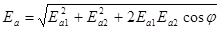 .(10.4)
.(10.4)
Если разность фаз в данной точке пространства постоянна, то амплитуда результирующего колебания в этой точке постоянна. В зависимости от разности фаз j в точке будет наблюдаться или усиление интенсивности света (j = 0, Еа = Еа1 + Еа2), или ослабление (j = p, Еа = Еа1 – Еа2). При равенстве амплитуд Еа1 = Еа2 и при j = p, Еа = Еа1 – Еа2 = 0. Происходит полное гашение света.
2.  Интерференционная картина. В реальных случаях складываемые волны сходятся обычно под некоторым углом друг к другу (рис.82). В результате в разных точках пространства А1, А2, А3… разность фаз j оказывается разной. Возникает пространственное распределение интенсивности света в виде чередующихся светлых и темных полос. Это так называемая интерференционная картина.
Интерференционная картина. В реальных случаях складываемые волны сходятся обычно под некоторым углом друг к другу (рис.82). В результате в разных точках пространства А1, А2, А3… разность фаз j оказывается разной. Возникает пространственное распределение интенсивности света в виде чередующихся светлых и темных полос. Это так называемая интерференционная картина.
Явление сложения волн с одинаковой частотой и постоянной во времени, достаточном для наблюдения, разностью фаз, при котором происходит перераспределение интенсивности в пространстве, называется интерференцией. Интерференционная картина наиболее контрастна, когда амплитуды складываемых волн одинаковы.
3. Когерентность (от лат. cohaerens – находящийся в связи) – согласованность во времени нескольких колебательных или волновых процессов, проявляющаяся при их сложении. Естественные источники света состоят из огромного количества хаотически вспыхивающих и потухающих излучателей – атомов и молекул. Через каждую точку оптически прозрачной среды, окружающей источник, проходят друг за другом цуги волн, испущенные разными атомами и имеющие разные амплитуды, фазы и частоты. Поэтому сделать два не лазерных источника света когерентными принципиально невозможно.
Получение когерентных лучей от естественных источников возможно путем расщепления луча от одного источника и создания между ними постоянного сдвига фаз. В этом случае лучи повторяют себя во всех деталях и потому могут интерферировать между собой.
Но при создании разности фаз надо помнить, что цуг волн, испущенный отдельным атомом, имеет конечную протяженность вдоль луча. При длительности испускания 10–11 ¸ 10–8 с эта протяженность не превышает 1 ¸ 3 м. Поэтому можно сказать, что через каждые 10-8 с волна, излучаемая даже одним атомом меняется.
Но даже отдельный цуг не есть отрезок синусоиды. Фаза колебания вектора Е на его протяжении непрерывно изменяется. Поэтому «голова» цуга не когерентна его «хвосту».
Время t, в течение которого фаза колебаний в световой волне, измеряемая в постоянной точке пространства, изменяется на p, называется временем когерентности. Расстояние сt, где с – скорость света, измеренное вдоль направления распространения волны, называется длиной когерентности. Свет разных источников имеет длину когерентности от нескольких микрометров до нескольких километров:
 – солнечный свет, сt » 1 ¸ 2 мкм,
– солнечный свет, сt » 1 ¸ 2 мкм,
– спектры разреженных газов, сt » 0,1 м,
– лазерное излучение, сt » 1 ¸ 2 км.
Для описания когерентных свойств волны в плоскости, перпендикулярной направлению ее распространения, применяют термин простран-ственная когерентность. Она определяется площадью круга диаметром l, во всех точках которого разность фаз не превышает величины p.
Пространство когерентности у точечного источника естественного света приближается к объему усеченного конуса длинной несколько мкм и диаметром основания несколько мм (рис.83). С удалением от источника оно увеличивается.
4.  Построение интерференционной картины методом Юнга. Первую схему двух-лучевой интерференции предложил в 1802 г. Томас Юнг. Он первый в ясной форме установил принципы сложения амплитуд и дал объяснение интерференции в волновой модели света. Суть схемы Юнга сводится к следующему.
Построение интерференционной картины методом Юнга. Первую схему двух-лучевой интерференции предложил в 1802 г. Томас Юнг. Он первый в ясной форме установил принципы сложения амплитуд и дал объяснение интерференции в волновой модели света. Суть схемы Юнга сводится к следующему.
Нормально лучам от естественного источника света устанавливается экран Э1 с узкой щелью S. Эта щель играет роль точечного источника света S. Распространяющаяся от S цилиндрическая волна возбуждает в щелях S1 и S2 экрана Э2 когерентные колебания. Поэтому волны, распростра-няющиеся от щелей S1 и S2, при взаимо-действии дают на экране Э3 интер-ференционную картину в виде системы параллельных щелям полос (рис.84).
Хотя на практике метод Юнга не применяется из-за слабой освещенности экрана Э3, он удобен для теоретического изучения двухлучевой интерференции с целью получения количественных оценок. Для этого представим схему Юнга в виде, показанном на рис.85.
Если S1 и S2 – когерентные источники света, излучающие в одинаковой фазе, то в любую произвольную точку А экрана Э3 будут приходить волны с разностью хода D = l2 – l1. Полагая на рисунке а<<L, из приближенного условия D/а = yçL получаем величину разности хода, D = аyçL. Она набегает тем больше, чем дальше точка наблюдения А от оси симметрии ОХ интерференционной картины (координата y), чем больше расстояние между щелями и чем ближе экран Э3 к щелям (расстояние L).
Максимум освещенности будет в тех точках экрана, где D составляет целое число волн, а минимум освещенности - где D составляет нечетное число полуволн.
 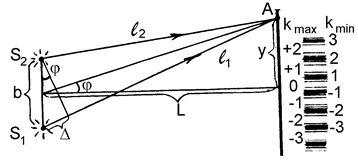 Рис.85 Рис.85
|
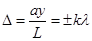 , k = 0, 1, 2, 3, (max), (10.5)
, k = 0, 1, 2, 3, (max), (10.5)
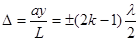 , k = 1, 2, 3,(min), (10.6)
, k = 1, 2, 3,(min), (10.6)
Здесь k – номер полосы. При малых углах j полосы располагаются равномерно. Расстояние между соседними темными или соседними светлыми полосами равно
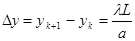 . (10.7)
. (10.7)
Оно тем больше, чем меньше расстояние а между источниками и чем больше расстояние L от источников до экрана.
При а = 1 мм, L = 1 м, Dу = 0,5×10–6×1ç10–3 = 0,5 мм для зеленых лучей.
5. Контрастность интерференционной картины зависит от протяженности источника света S и от степени монохроматичности света.
а. Влияние немонохроматичности света. В том случае, когда интерферируют немонохроматичные волны, максимумы на экране для разных длин волн не совпадают. В результате интерференционная картина размывается. Она полностью смазывается, когда на k-ый максимум волны с длиной l + Dl приходится k + 1-й максимум волны с длиной l.
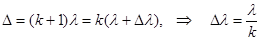 . (10.8)
. (10.8)
Все пространство минимума для волны l занято максимумами с длинами от l до l + Dl.
 Критерий монохроматичности ограничивает число наблюдаемых полос. Например для солнечного света с l от 0,4 до 0,8 мкм весь спектральный диапазон можно представить в виде: l = l0 ± Dl = 0,6± 0,2 мкм. Максимальный порядок наблюдающейся интерференционной полосы kmax = l0 / Dl = 0,6/0,2 = 3. Значит, могут наблюдаться 6 темных полос, соответствующих k = –3, –2, –1, +1, +2, +3.
Критерий монохроматичности ограничивает число наблюдаемых полос. Например для солнечного света с l от 0,4 до 0,8 мкм весь спектральный диапазон можно представить в виде: l = l0 ± Dl = 0,6± 0,2 мкм. Максимальный порядок наблюдающейся интерференционной полосы kmax = l0 / Dl = 0,6/0,2 = 3. Значит, могут наблюдаться 6 темных полос, соответствующих k = –3, –2, –1, +1, +2, +3.
Сжимая с помощью светофильтров спектральный интервал, можно увеличить число и контрастность наблюдаемых полос.
б. Влияние протяженности источника. Пусть ширина щели S равна b (рис.86). Чтобы щели S1 и S2 излучали в одной фазе, нужно, чтобы лучи, приходящие в каждую щель от разных точек источника S, имели малую разность хода D, не более четверти длины волны. 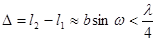 . (10.9)
. (10.9)
Угол w обычно не больше 1°. Поэтому ограничение по ширине щели можно записать так: 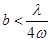 . Но w = аç2d, где а - расстояние между щелями S1 и S2, d - расстояние от щели S до S1 и S2. Тогда b<ldç2a (10.10)
. Но w = аç2d, где а - расстояние между щелями S1 и S2, d - расстояние от щели S до S1 и S2. Тогда b<ldç2a (10.10)
При а =1 мм, d = 1 м, l = 0,6×10–6 м, b<0,6×10–6×1ç2×10–3 = 0,3×10–3 м = 0,3 мм. Для получения хорошей контрастности эта величина должна быть уменьшена еще в 3-4 раза.
6.  Практические методы наблюдения интерференции.
Практические методы наблюдения интерференции.
а. Бизеркала Френеля, 1816 г. (рис.87). Свет от источника, заключенного в светонепроницаемый кожух, через отверстие в нем попадает расходящимся пучком на два плоских зеркала. Угол между зеркалами a » 179°.
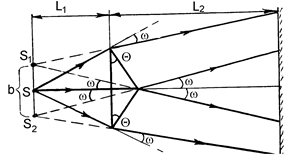 Рис.88 Рис.88
|
Достоинство метода – хорошая освещен-ность, недостаток – сложность юстировки зеркал на оптической скамье.
б. Бипризма Френеля, 1819 г. (рис.88). Достоинства – хорошая освещенность и простота юстировки, недостаток – требуется специальная бипризма, изделие оптической промышленности.
Здесь S1 и S2– мнимые изображения источника света S.
 в. Билинза Бийе, 1845 г. (рис.89). Собирающая или рассеивающая линза разрезается (раскалывается) по диаметру, и обе половины слегка раздвигаются в стороны.
в. Билинза Бийе, 1845 г. (рис.89). Собирающая или рассеивающая линза разрезается (раскалывается) по диаметру, и обе половины слегка раздвигаются в стороны.
 Чем дальше раздвинуты друг от друга полулинзы, тем сильнее сжата интерференцион-ная картина, тем уже полосы. Здесь S1 и S2 – действительные изображения источника света S.
Чем дальше раздвинуты друг от друга полулинзы, тем сильнее сжата интерференцион-ная картина, тем уже полосы. Здесь S1 и S2 – действительные изображения источника света S.
г. Зеркало Ллойда, 1837 г. (рис.90). Прямой пучок от источника S интерферирует с пучком, отраженным от зеркала.
Здесь S – освещенная щель, S1– ее мнимое изображение.
Дата добавления: 2020-05-20; просмотров: 580;











