Диаграммы рассеивания

На практике в ходе анализа процессов бывает важно изучить зависимость между двумя переменными. Например, необходимо установить, зависит ли разброс размеров детали от изменения числа оборотов шпинделя, связана ли долговечность детали с температурными условиями её эксплуатации и т. п. Для изучения подобных зависимостей используются диаграммы рассеивания.

Диаграмма рассеивания – это графическое представление множества данных, которые отражают связь между двумя факторами.

В общем случае, методика построения диаграмм рассеяния состоит из следующих этапов:

1) сбор исходных данных (х и у);

2) построение диаграммы вида (рис. 8.1). Каждая точка имеет координаты (х, у), где х – фактор, у – показатель качества, а всё поле точек позволяет судить о наличии или отсутствии связи между переменными;

3) Выполнение анализа диаграммы:

- исключение из рассмотрения всех точек, которые далеко отстоят от основной группы (например, точка * (x₂, y₂) на рис. 8.1);

- поиск причин появления таких точек (ошибки измерения или записи данных, особые причины и др.);

- определение наличия (отсутствия) связи между переменными и её характера.

Рис. 8.1. Пример диаграммы рассеяния

При анализе связи между переменными возможны различные варианты скопления точек (рис. 8.2): а) положительная корреляция; б) отрицательная корреляция; в) корреляции нет.

Рис. 8.2. Варианты скоплений точек на диаграмме рассеяния

Корреляция означает, что между переменными есть линейная зависимость, причём чем уже поле рассеяния точек, тем больше корреляция. В этом случае, управляя одним фактором, можно влиять на другой. Вместе с тем, следует принимать во внимание наличие ряда ограничений, связанных с корреляционным анализом данных:

- применение возможно в случае наличия достаточного количества случаев для изучения (от 25 до 100 пар наблюдений);

- второе ограничение вытекает из гипотезы корреляционного анализа, в которую заложена линейная зависимость переменных. Во многих случаях, когда достоверно известно, что зависимость существует, корреляционный анализ может не дать результатов ввиду того, что зависимость не линейна (рис. 8.3);

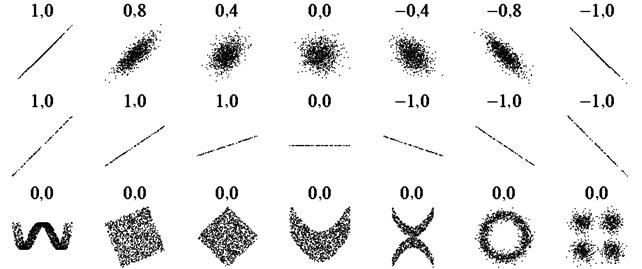
Рис. 8.3. Коэффициенты корреляции для различных форм рассеяния точек

- сам по себе факт корреляционной зависимости не даёт основания утверждать, какая из переменных предшествует или является причиной изменений, или что переменные вообще причинно связаны между собой, например ввиду действия третьего фактора. Например, в одном исследовании была установлена корреляция между индексом потребительских цен и числом пожаров. Если бы это было так, то при снижении индекса наблюдалось бы и уменьшение числа случайных возгораний. Поэтому если между двумя переменными наблюдается корреляционная зависимость, не подкреплённая причинно-следственной связью, то в этом случае можно говорить о ложной корреляции.

Гистограммы

Гистограммы используют, чтобы судить о том, является ли процесс стабильным, настроенным, появляется ли брак. Это один из самых эффективных инструментов для управления ходом технологического процесса или операции.

Гистограмма – это столбчатая диаграмма, показывающая число точек, попадающих в заданные интервалы. Число точек в интервале называют частотой.

Если процесс стабилен, его гистограмма имеет форму колоколообразной кривой. При этом, если весь диапазон гистограммы
разделить на 6 равных отрезков (по три с каждой стороны от центра), то данные распределятся так, как показано на рис. 8.4.

Рис. 8.4. Пример гистограммы стабильного процесса

Построение гистограммы включает ряд основных этапов.

1) Составляется таблица исходных данных.

2) Вычисляется выборочный размах

R = [наибольшее значение] – [наименьшее значение].

3) Определяется ширина интервалов гистограммы. Приблизительная ширина интервала определяется по формуле:

,

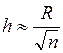где п – количество данных (т. е. объём выборки, умноженный на число выборок).

4) Подсчитывается число попавших в каждый интервал значений (частоты).

5) Строится гистограмма, на которой откладываются среднее арифметическое и границы допуска.

6) Производится анализ гистограммы (определение закона рассеяния данных и сравнение положения гистограммы с границами допуска).

Различают несколько типичных форм гистограмм, в частности (рис. 8.5):

а) гистограмма с двусторонней симметрией (нормальное распределение). Гистограмма с таким распределением встречается чаще всего. Она указывает на стабильность процесса;

б) гистограмма с ненормально высоким краем. Такая гистограмма отражает случаи, когда была допущена ошибка при измерениях, когда наблюдались отклонения от нормы в ходе процесса и т. д.;

в) гистограмма, вытянутая вправо (влево). Такую форму с плавно вытянутым основанием гистограмма принимает в случае, когда невозможно получить значения меньше (больше) определённого – например, для диаметра отверстий, процента содержания примесей в металле.

Рис. 8.5. Типичные формы гистограмм

Таким образом, форма гистограммы позволяет получить информацию о законе распределения размеров и о наличии или отсутствии отклонений в ходе процесса.

Дальнейший анализ процесса с помощью гистограмм может выполняться сравнением гистограмм с границами допуска. Если нанести на гистограмму линии границ допуска, то можно увидеть, как гистограмма располагается внутри границ, имеется ли брак, есть ли запас по точности и др.

Если гистограмма удовлетворяет допуску, то возможны следующие случаи (рис. 8.6):

а) центр гистограммы совпадает с серединой поля допуска. Поле рассеяния небольшое. В этом случае достаточно поддерживать текущее состояние;

б) допуск выдерживается, но нет никакого запаса. Следует уменьшить разброс значений, иначе возможно появление брака.

Если гистограмма не удовлетворяет допуску, ситуации могут быть следующими:

в) разброс размеров небольшой, но центр рассеяния смещён в сторону. Появляется брак. Необходимо сместить центр рассеяния к середине поля допуска;

г) центр рассеяния совпадает с серединой поля допуска, но разброс слишком велик. Появляется брак. Необходимо уменьшить разброс размеров;

д) комбинация вариантов в) и г). То есть необходимо одновременно сместить центр рассеяния к середине поля допуска и при этом уменьшить разброс размеров.

Рис. 8.6. Варианты расположения гистограмм и границ поля допуска:
НГД и ВГД – соответственно нижняя и верхняя границы поля допуска,