Расчет коэффициентов уравнения регрессии методом наименьших квадратов

Метод наименьших квадратов (МНК) может быть использован для расчета коэффициентов уравнения регрессии, выраженного в виде полинома степени m.

Рассмотрим пример определения коэффициентов однофакторного уравнения регрессии вида у = а₀ + а₁ × х. Фактические значения фактора x и результата y приведены в форме таблицы (таблица 8.3).

При определении коэффициентов однофакторного уравнения регрессии с помощью табличных (фактических) значений определяют регрессионные остатки e, характеризующие отклонения, с которыми полиномиальное уравнение регрессии отображает табличную функцию. Таким образом, для каждой из n множества пар значении x – y получаем соответствующее значение регрессионного остатка e .

Таблица 8.3 – Исходные данные для определения
коэффициентов уравнения регрессии

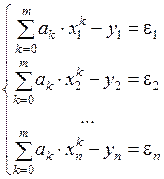
Ясно, что чем лучше будут подобраны коэффициенты полиномиального уравнения регрессии, тем меньше по абсолютной величине будут отклонения. Поэтому требуется найти такие значения коэффициентов a_k (k = 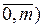, при которых сумма квадратов регрессионных остатков была бы минимальной:

.

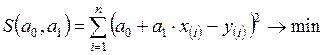Функция двух аргументов S (а₀, а₁) принимает экстремальное значение, в данном случае минимальное, в точке (а₀, а₁), в которой частные производные этой функции по каждому аргументу равны нулю:

,

.

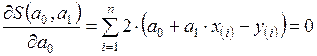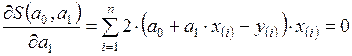После преобразования получаем систему уравнений:

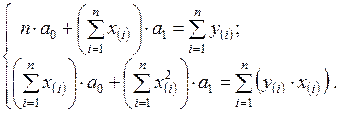
Решая систему двух линейных уравнений относительно двух неизвестных а₀ и а₁, определяем коэффициенты (параметры) линейного уравнения регрессии.