Воспроизводимость процесса
Воспроизводимый процесс – это такой процесс, разброс которого имеет колоколообразную форму и укладывается в поле допуска. Анализ воспроизводимости выполняется с целью:
- оценки нового оборудования;
- распределения оборудования по продукции (более стабильное оборудование для особо точных работ);
- отслеживания текущих показателей процесса;
- пересмотра допусков на основе внутренней изменчивости процесса.
Для анализа воспроизводимости рассчитывается индекс воспроизводимости процесса Cp, оценивающий возможности удовлетворять технический допуск без учета положения среднего значения и применяемый для стабильных по разбросу процессов (ГОСТ Р 50779.44-2001 «Статистические методы. Показатели возможностей процессов»):
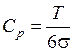 ;
; 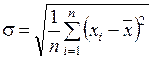 ;
; 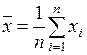
где Т – допуск; s – стандартное отклонение (мера рассеяния данных); 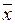 – среднее арифметическое (мера центра распределения); хi – отдельные значения выборки; п – объём выборки.
– среднее арифметическое (мера центра распределения); хi – отдельные значения выборки; п – объём выборки.
Среднее арифметическое позволяет определить, насколько смещён центр группирования размеров относительно середины поля допуска, а s определяет разброс данных. Чем больше s, тем шире и ниже кривая нормального распределения; чем s меньше, тем кривая выше и уже.
Процесс считается воспроизводимым при Ср > 1,33; управляемым при жёстком контроле при Ср Î[1, 1,33]; неуправляемым при Ср < 1.

Рис. 8.7. Положения кривой рассеяния данных
при разных индексах воспроизводимости
Как видно из рис. 8.7 значение Ср = 1 не дает гарантии от возникновения брака из-за возможного смещения кривой распределения относительно центра допуска. Для оценки таких ситуаций используют другой индекс воспроизводимости, а именно:
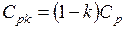 , где
, где 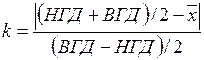 .
.
По известному значению индексов воспроизводимости можно оценить ожидаемый уровень несоответствий продукции (таблица 8.5).
Таблица 8.5 – Связь индексов воспроизводимости стабильных процессов
с ожидаемым уровнем несоответствий продукции
| Значение Ср или Срk | Уровень несоответствий продукции в | |
| процентах | единицах на миллион | |
| 0,33 | 32,2 | |
| 0,55 | 9,9 | |
| 0,75 | 2,4 | |
| 1,00 | 0,27 | |
| 1,33 | 0,0066 |
Контрольные карты
Как и гистограммы, контрольные карты – эффективный инструмент для управления ходом процесса. Они были предложены американским учёным Уолтером Шухартом в 1924 г. и часто называются его именем.
Назначение контрольных карт – дать возможность определить, находится ли процесс в статистически управляемом состоянии, и если да, то не собирается ли он из него выйти.
Предположим, что в некотором процессе систематически регистрируются результаты измерений. Измеряемыми величинами могут быть диаметр обработанного вала, затраты времени на обслуживание станка, процент дефектных изделий в партии, и т. д. и т. п. В процессе измерений строятся графики (рис. 8.8). По горизонтальной оси откладывается время, по вертикальной – размеры деталей, затраты времени, процент дефектных изделий или другие регистрируемые величины.

Рис. 8.8. Примеры графиков изменения регистрируемых величин
На первом графике (рис. 8.8) показан типичный пример управляемого процесса. На 2 и 3-м графиках показаны процессы, находящиеся в статистически неуправляемом состоянии. На всех графиках в измерениях имеются вариации. Отличие заключается в том, что на первом характер вариаций сохраняется в течение всего периода наблюдений, а на втором и третьем характер вариаций заметно изменяется.
В первом случае есть возможность спрогнозировать будущие результаты процесса. В двух других случаях невозможно сделать никакого прогноза, поскольку поведение этих процессов изменяется совершенно непредсказуемым образом, т. е. нельзя предсказать, какими будут средние значения, а также каков будет разброс относительно этих средних.
Таким образом, процесс находится в состоянии статистического контроля (т. е. является статистически управляемым), если лежащее в его основе распределение остается практически неизменным во времени (рис. 8.9, а), т. е. когда действуют только обычные (случайные) причины вариации. Если распределение меняется существенно и непредсказуемо, то говорят, что процесс вышел из-под контроля (т. е. стал неуправляемым) (рис. 8.9, б). Такое случается, если имеются особые причины вариации.

Рис. 8.9. Примеры управляемых и неуправляемых процессов
В случае неуправляемого процесса невозможно оценить результат замены оборудования, замены сырья или любых других изменений, которые могут быть проведены с целью улучшения процесса. Пока процесс находится в неуправляемом состоянии, нельзя предсказать его возможности. Если особые причины были устранены, тогда улучшения могут зависеть от принимаемых мер, поскольку в этом случае разброс процесса определяется тем, каким образом этот процесс был спроектирован и построен.
Для того отличить особые причины вариаций от случайных и определить, когда нужно вмешиваться в ход процесса, а когда вмешательство нежелательно, целесообразно использовать один из статистических инструментов управления процессами, например, контрольные карты.
Контрольные карты – это линейные графики, показывающие динамику поведения процесса. При их использовании различают два вида изменчивости.
1) Изменчивость из-за случайных (обычных) причин, обусловленная бесчисленным набором разнообразных причин, присутствующих постоянно, которые нелегко или невозможно выявить. Каждая из таких причин составляет очень малую долю общей изменчивости, и ни одна из них не значима сама по себе. Тем не менее, сумма всех этих причин измерима, и предполагается, что она внутренне присуща процессу. Исключение или уменьшение влияния обычных причин требует улучшения процесса и системы.
2) Реальные перемены в процессе. Они могут быть следствием некоторых причин, не присущих процессу внутренне, и могут быть устранены. Эти причины рассматриваются как «неслучайные» или «особые». К ним могут быть отнесены поломка инструмента, недостаточная однородность материала, производственного или контрольного оборудования, квалификация персонала, невыполнение процедур и т. д.
Цель контрольных карт – обнаружить неестественные изменения в результатах процесса и определить отсутствие статистической управляемости. Процесс находится в статистически управляемом состоянии, если изменчивость вызвана только случайными причинами.
Любая контрольная карта состоит из центральной линии, двух контрольных пределов – выше и ниже неё, и значений показателя качества, нанесённых на карту для представления состояния процесса. Если все эти значения оказываются внутри контрольных пределов, не проявляя каких бы то ни было тенденций, то процесс рассматривается как находящийся в контролируемом состоянии. Если же, напротив, они попадут за контрольные пределы или примут какую-либо необычную форму, то процесс считается вышедшим из-под контроля.
Существует масса всевозможных карт. Их делят на два основных типа.
1) Контрольные карты для количественных переменных. Они отражают конкретные измерения характеристик (твёрдость, размер, масса и т. п.). К таким картам относятся:
- 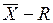 -карты (когда данные легко доступны);
-карты (когда данные легко доступны);
- 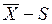 -карты (когда s легко доступно);
-карты (когда s легко доступно);
- карты медиан и др.
2) Контрольные карты для качественных переменных. Эти карты применяются в тех случаях, когда показатель качества представлен числом дефектных изделий. К ним относятся: р-карты, с-карты, пр-карты и и-карты (где р – доля дефектов, с – число дефектов, пр – число дефектных изделий, и – процент дефектных изделий).
Карты для количественных переменных обычно обходятся дороже, поскольку надо собрать и проанализировать данные для каждого признака качества. Но эти карты более информативны и полезны.
Рассмотрим вариант управления технологическим процессом с помощью 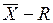 -карт. (
-карт. ( 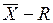 означает, что одновременно используются две карты – карта средних арифметических и карта размахов).
означает, что одновременно используются две карты – карта средних арифметических и карта размахов).
1) Получение исходных данных. При управлении процессом с помощью контрольных карт периодически берут выборку обработанных деталей и измеряют параметр качества. Данные заносят в таблицу
(таблица 8.6).
Таблица 8.6 – Исходные данные для построения контрольных карт
| № выборки | Х1 | Х2 | Х3 | 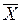
| R |
| 10,26 | 10,31 | 10,35 | 10,31 | 0,09 | |
| 10,29 | 10,34 | 10,32 | 10,32 | 0,05 | |
| … | … | … | … | … | |
| Итого: | 92,94 | 0,72 |
2) Подсчёт среднего арифметического 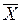 и размаха R для каждой выборки. Полученные значения заносят в соответствующие столбцы таблицы исходных данных (таблица 8.6).
и размаха R для каждой выборки. Полученные значения заносят в соответствующие столбцы таблицы исходных данных (таблица 8.6).
3) Подсчёт общего среднего 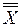 – это будет центральная линия на карте средних арифметических. Для этого сумму столбца
– это будет центральная линия на карте средних арифметических. Для этого сумму столбца 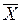 делят на число выборок:
делят на число выборок:
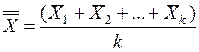 ,
,
где k – число выборок.
4) Подсчёт среднего размаха. Аналогичным образом делят сумму размахов на число выборок: 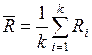 . Это будет положение средней линии на карте размахов.
. Это будет положение средней линии на карте размахов.
5) Вычисление контрольных линий.
Для 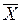 -карты:
-карты:
верхний контрольный предел 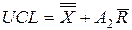 ,
,
нижний контрольный предел 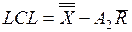 .
.
Для R-карты:
верхний контрольный предел 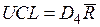 ,
,
нижний контрольный предел 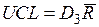 .
.
Константы А2, D4, D3 определяются объёмом выборки (таблица 8.7).
Таблица 8.7 – Значения констант для расчёта контрольных линий
| n | A2 | D4 | D3 |
| 0,577 | 2,115 | – | |
| 0,483 | 2,004 | – | |
| 0,419 | 1,924 | 0,076 | |
| 0,373 | 1,864 | 0,136 | |
| 0,337 | 1,816 | 0,184 |
6) Построение контрольных карт. По горизонтальной оси откладывают номера выборок, по вертикальной – контрольные линии карт (рис. 8.10). Среднюю линию выполняют сплошной, верхний и нижний контрольные пределы – пунктиром. Области между контрольными пределами и средней линией делят на три равные зоны с обеих сторон. Зоны С располагаются возле центральной линии, зоны А – возле контрольных пределов. Ширина каждой зоны составляет 1s, а всей контрольной карты – 6s.
Далее на карту средних наносят точки, соответствующие выборочным средним, а на карту размахов, соответственно, размахам выборок. Полученные точки соединяют линиями.

Рис. 8.10. Примеры построения карт средних и размахов
7) Интерпретация карт. Поскольку контрольные карты нужны для отслеживания состояния процесса и немедленного реагирования при проявлении особых причин, необходимо знать, как отличить действие особых причин от вариаций, обусловленных случайными причинами. Для этого используется ряд критериев, основанных на том, что вероятность появления некоторых вариантов расположения точек очень мала, и эти варианты могут встретиться только в том случае, если на процесс оказывают влияние какие-то особые причины. Перечислим некоторые из этих критериев.
1) Точка за контрольными пределами.Поскольку общая ширина контрольной карты составляет 6s, то вероятность выхода даже одной точки за контрольные пределы крайне мала, если действуют только случайные причины.
2) 2 из 3-х расположенных подряд точек попадают в зону A или выходят за её пределы. Этот критерий служит «ранним предупреждением» о начинающейся разладке процесса (рис. 8.11, а).

а) б)
Рис. 8.11
3) 9 и более точек по одну сторону центральной линии. Такое расположение точек называют серией (рис. 8.11, б). Данное отклонение может проявляться и в некоторых других случаях, например: 10 из 11 последовательных точек оказываются по одну сторону от центральной линии; или 12 из 14 точек, или 16 из 20.
4) Тренд (7 и более непрерывно повышающихся или понижающихся точек).Такое расположение точек сигнализирует о сдвиге среднего значения процесса (рис. 8.12, а). Часто такой сдвиг обусловлен износом инструмента, ухудшением технического обслуживания оборудования, повышением квалификации рабочего.

а) б)
Рис. 8.12
5) 14 попеременно возрастающих и убывающих точек. Такой критерий указывает на действие двух систематически изменяющихся причин, приводящих к получению различных результатов (рис. 8.12, б). Например, использование двух поставщиков сырья или двух рабочих.
6) Четыре из пяти последовательных точек в зоне В или вне её(рис. 8.13, а).
7) Восемь последовательных точек по обеим сторонам центральной линии и ни одной в зоне С (рис. 8.13, а). Такой критерий служит свидетельством того, что различные выборки подвержены влиянию различных факторов, в результате чего средние значения оказываются распределены по бимодальному закону (образуется двухпиковая гистограмма). Такое может получиться, например, при обработке на двух станках, один из которых производит изделия с контролируемым параметром ниже среднего, а другой – выше.
8) 15 последовательных точек в зоне С выше и ниже центральной линии (рис. 8.13, б). Появление такой последовательности указывает на более низкую изменчивость по сравнению с ожидаемой (на основании выбранных контрольных пределов).

а) б)
Рис. 8.13
Этот набор критериев можно принять за основу, но вообще следует обращать внимание на любую необычную структуру точек, которая может указывать на проявление неслучайных причин.
Также следует учитывать и ещё один момент. То, что процесс находится в управляемом состоянии, не означает, что в продукции не появится брак. И наоборот, если процесс вышел из-под контроля, это не значит, что обязательно получатся бракованные изделия. Процесс находится под контролем, когда действуют только случайные причины, и при этом он проявляет наименьший разброс, на который способен. Контрольные пределы лишь показывают вариацию, обусловленную случайными причинами. Границы же допуска определяются техническими условиями.
Таким образом, могут встретиться 4 варианта:
- процесс неуправляемый, производится брак;
- процесс управляемый, брака нет;
- процесс управляемый, производится брак;
- процесс неуправляемый, брака нет.
В двух последних случаях налицо несовпадение границ допуска и воспроизводимости процесса. При этом в случае управляемого процесса, выдающего брак, необходимо улучшить воспроизводимость процесса, то есть уменьшать разброс от действия случайных причин. Поскольку процесс управляемый, меры по его улучшению будут давать эффект. Следовательно, можно, например, заменить оборудование на более точное, изменить конструкцию приспособления, чтобы снизить погрешность установки заготовки и др. В случае же неуправляемого процесса, работающего без брака, мы всего лишь видим, что допуск достаточно велик, чтобы даже нестабильный процесс производил годную продукцию. Всё же необходимо выявлять особые причины и добиваться того, чтобы он стал управляемым. Ведь иначе нет никакой гарантии, что брак так и не появится. Кроме того, улучшение такого процесса позволит уменьшить поле допуска.
Дата добавления: 2018-11-26; просмотров: 3765;











