Колебания в упругой среде. Волны

1. Сжимаемость жидкостей и газов.Реальные жидкости и газы сжимаемы, то есть под действием внешней силы могут уменьшать свой объем. Наиболее заметна их сжимаемость при скоростях движения тел или частиц среды, близкой к скорости звука в данной среде.

Если в какой-то точке сплошной упругой среды тело или частица среды колеблются около положения равновесия, то их колебания передаются другим частицам среды. В результате в среде распространяется волна. Кинематическим признаком волнового движения является распространение фазы колебаний, динамическим – перенос энергии.

2. Волновая поверхность. Геометрические виды волн. Воображаемая поверхность, в каждой точке которой частицы среды колеблются в одной фазе, называется волновой поверхностью. В зависимости от формы волновой поверхности различают плоские, сферические и цилиндрические волны.

а. Плоская волнаизлучается (генерируется) колеблющейся плоской поверхностью (рис.106). Если стенка колеблется по гармоническому закону x = Acosw t, (31.1)

где x – смещение стенки относительно положения равновесия вдоль оси ОХ, то колебания частиц среды будут отставать по фазе в зависимости от расстояния до стенки X. Время отставания t¢=x/v. Так что колебания любой точки среды описываются уравнением

x=Acosw 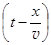. (31.2)

Это уравнение плоской гармонической монохроматической волны, которая распространяется в среде без затухания. Минимальное расстояние между однофазными волновыми поверхностями называют длиной волны l, а их скорость перемещения называют фазовой скоростью v. (рис.107) Фазовая скорость, длина волны и частота колебания частиц связаны между собой: v =ln. (31.3)

б. Сферическая волна генерируется шаровым телом или сферической поверхностью (рис.108). Уравнение сферической волны в среде без затухания имеет вид:

x=A₀ 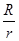cosw 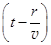, r >> R. (31.4)

Убывание амплитуды по мере удаления волны от центра объясняется возрастанием волновой поверхности с ростом r, в результате энергия волнового движения распределяется на все большее число частиц.

в. Цилиндрическая волна (рис.109) генерируется боковой поверхностью длинного цилиндра. Уравнение цилиндрической волны в среде без затухания имеет вид:

x =A₀ 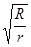cosw 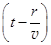. (31.5)

3. Продольные и поперечные волны. В зависимости от направления смещения частиц среды упругие волны бывают продольными и поперечными.

а. В продольной волне частицы среды колеблются вдоль направления распространения волны (рис.110). Это так называемые волны сжатия. Продольные волны могут распространяться в твердых, жидких и газообразных телах. Скорость распространения продольной волны 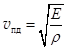, (31.6)

где Е – модуль Юнга, если волна распространяется в твердом теле, или модуль всестороннего сжатия, если волна распространяется в жидкости или в газе, r – плотность среды.

б. В поперечной волне частицы отклоняются от положения равновесия в направлении, перпендикулярном направлению распространения волны (рис.111). Скорость поперечной волны определяется формулой: 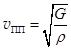. (31.7)

Здесь G – модуль сдвига среды, r – плотность среды.

Поперечные волны могут существовать только в твердых упругих телах.

4. Стоячие волны. Если волна распространяется в ограниченном пространстве, то могут возникать ситуации, когда из бегущей волны формируется стоячая волна (рис.112).

Для появления стоячих волн нужно, чтобы бегущая волна отражалась от границы среды без затухания и чтобы на отрезке между стенкой-генератором и стенкой-отражателем укладывалось целое число полуволн, l =N 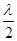. (N=1, 2, 3, ..) (31.8)

Координаты пучностей х_пучн = n 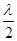, (n=0, 1, 2, ..)(31.9)

Координаты узлов х_узлов= 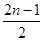× 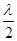, (n=1,2,3,..) (31.10)

Немецкий физик Эрнст Хладни (I756–I827) предложил в 1787 году метод наблюдения схемы расположения стоячих волн в упругих пластинках. Если на горизонтально расположенную пластинку насыпать песок и провести по ее краю смычком, то при колебаниях пластинки частицы песка соберутся в области узлов. На поверхности пластинки появляются так называемые фигуры Хладни (рис.113).

5. Энергия бегущей волны. Вектор Умова. Энергетический поток бегущей упругой волны нашел теоретическим путем в 1874г. русский физик Николай Умов (I846–I9I5). Средняя плотность потока энергии, т.е. количество энергии, переносимое бегущей волной через единичную площадку в единицу времени, определяется выражением:

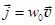. Вектор Умова, 1874 (31.11)

Здесь w₀ – средняя плотность энергии волны, v – скорость.

Если вместо средней плотности энергии использовать мгновенную плотность энергии, то формула вектора Умова будет выражать мгновенную плотность потока энергии.

Найдем зависимость среднего значения вектора Умова от параметров волны.

Величина w₀ определяет механическую энергию единицы объема среды. Как известно, механическая энергия гармонического осциллятора составляет E = mA² 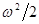. Применительно к единице объема среды m=r, и средняя плотность энергии w₀ =rA² 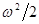. Отсюда среднее значение плотности потока энергии бегущей волны равно

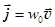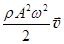= . (31.12)

Количество энергии, переносимое бегущей волной через поверхность S в единицу времени, есть поток энергии (рис.114)

F = jScos( 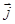^ 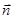) = j_nS. (31.13)

Здесь n – единичный вектор нормали к площадке. В качестве примера найдем, как изменяется амплитуда колебания частиц среды в сферических и цилиндрических волнах.

Пример 31.1. Сферическая волна. Поскольку среда без затухания, то поток энергии через любую сферу, охватывающую излучатель, равна потоку энергии от излучателя:

F = jS = .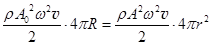

Здесь A₀ – амплитуда колебаний поверхности сферы-генератора, А – амплитуда колебания частиц среды, R – радиус сферы-генератора (рис.115). Отсюда

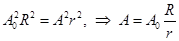. (31.14)

Пример 31.2. Цилиндрическая волна. Если излучающий цилиндр достаточно длинный, то можно считать, что вся энергия волны распространяется в радиальных направлениях. Тогда F = jS = 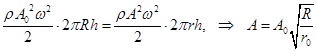. (31.15)

Здесь R – радиус цилиндра-генератора, h – его высота (длина).

6. Затухающие волны. Если среда вязкая, то механическая энергия упругой волны постепенно рассеивается, то есть превращается в тепло. Амплитуда плоской волны уменьшается с расстоянием до стенки-излучателя (рис.116).

Уравнение плоской бегущей волны в вязкой среде имеет вид: 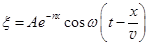. (31.16)

Здесь n – коэффициент затухания волны.

Определим расстояние l, на котором амплитуда колебания частиц среды уменьшается в е раз. Полагаем затухание слабым, так что l >> l. Поэтому без большой погрешности можно принять, что на отрезке l укладывается целое число волн, l = Nl. Это позволяет сравнивать амплитуды частиц, колеблющихся в одной фазе.

Запишем уравнение волны для частиц с координатами х и х + l.

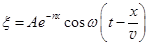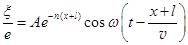, . (31.17)

Разделим 1-е уравнение на 2-е. Так как частицы колеблются в одной фазе, то косинусы сокращаются. Получаем e = e^nl, Þ nl = 1, и n = . (31.18)

Итак, коэффициент затухания n есть величина, обратная отрезку, на котором амплитуда волны уменьшается в e раз.