Звуковые волны. Акустика

1. Природа звука. Звук – явление, воспринимаемое специальным органом чувств человека и животных. Звуковые волны в воздухе представляют собой продольные механические волны. Они испускаются источником звука – колеблющимся телом – и распространяются в твердых телах, жидкостях и газах в виде колебаний давления.

Обычное человеческое ухо воспринимает звуковые колебания в диапазоне частот от 16 до 20 000 Гц. Поскольку звуковые волны – это обычные волны упругости, то к ним применима вся теория упругих волн. Но поскольку волны указанного диапазона имеют большое значение в жизни людей, то теория звуковых волн выделилась исторически в особый раздел – акустику (от греческого akustikos – слуховой).

Упругие колебания частотой более 20 000 Гц называют ультразвуком, а частотой менее 16 Гц – инфразвуком.

2. Источники звука. Это колеблющиеся тела, возбуждающие в среде звуковые волны. Они могут быть твердыми (струна, стержень, пластина), газообразными (струя реактивного двигателя, столб воздуха) и жидкими (водопад). Рассмотрим примеры:

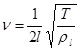а. Струна с закрепленными концами(рис.117). Частота основного тона свободно колеблющейся струны определяется формулой: , (32.1)

где l – длина струны, Т – сила ее натяжения, r_l – линейная плотность струны (масса единицы длины).

Кроме основного тона, когда на струне возникает стоячая полуволна, l = 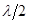, струна может излучать и более высокие тоны (обертоны), когда на струне возникает 2, 3, 4 и т.д., то есть любое целое число стоячих полуволн. Общая формула собственных частот колебаний струны: 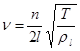. (32.2)

Число n показывает количество стоячих полуволн на струне.

б. Камертон. Представляет собой стальной стержень, изогнутый в виде латинской буквы U (рис.118). Середина стержня закрепляется неподвижно, а концы остаются свободными и могут колебаться. Поскольку собственная частота колебаний камертонов очень слабо зависит от внешних воздействий, то их используют, в основном, в качестве эталонных источников звука. Чаще всего камертоны настраивают на частоту 440 Гц.

в. Звучащие пластины используются в литаврах, ксилофонах, металлофонах.

г. Столб воздуха звучит в духовых музыкальных инструментах, органных трубах, свистках.

3. Скорость звука в газах. Распространение звука в газах – адиабатный процесс (теплопроводность не играет роли), для которого модуль всестороннего сжатия E = gp. Здесь g – показатель адиабаты. Для двухатомных газов, в том числе и для воздуха, g = 1,4. Для одноатомных газов g =1,66 (гелий, неон, пары металлов), для многоатомных газов g =1,33 (углекислый газ, пары воды, метан и др. углеводороды). Формула скорости звука в газах имеет вид: 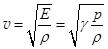. (32.3)

Если давление p выразить из уравнения Клапейрона-Менделеева, то 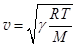(32.4)

Здесь R = 8,31 Дж/(К×моль) – универсальная газовая постоянная, М – молярная масса газа, Т – его абсолютная температура. При Т = 273 К скорость звука в воздухе составляет 332 м/с.

4. Характеристики звука. Поскольку звук – объективный волновой процесс, то к нему применимы все характеристики упругих волн. Наряду с кинематическими – скоростью, частотой, фазой, длиной волны – звук характеризуется и энергетическими величинами – интенсивностью и звуковым давлением.

а. Интенсивность звука – это средняя плотность потока энергии, иначе, это среднее по времени значение вектора Умова. I= 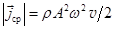. (32.5)

Единица измерения I в СИ – Вт/м². Принято считать стандартным порогом слышимости человеческого уха интенсивность I₀ = 1 пиковатт/м². Интенсивность 10 Вт/м² вызывает боль в ушах и называется порогом болевого ощущения.

б. Среднее звуковое давление – это среднее по времени среднеквадратичное избыточное давление в газе, обусловленное волновым процессом. Между средним звуковым давлением и интенсивностью звука существует связь: 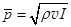. (32.6)

Стандартное пороговое звуковое давление составляет 2×10^–5 Па, порог болевого ощущения по среднему звуковому давлению составляет @100 Па. (Все данные для частоты 1000 Гц).

в. Уровень интенсивности L, есть логарифм десятичный отношения интенсивности звука I к стандартному порогу слышимости I₀, то есть L=lg( 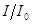). (32.7)

Единица измерения уровня интенсивности – бел (Б). Это безразмерная величина, названа так в честь изобретателя телефона шотландца (по рождению) Александра Белла (I847–I922). Белл – очень крупная единица, весь диапазон уровней интенсивности, воспринимаемых человеческим ухом, составляет всего 13 бел. Поэтому на практике используют величину в 10 раз меньшую – децибел, 1 дБ = 0,1 Б. Выражение для L в децибелах принимает вид: L=10×lg( 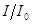) дБ. (32.8)

5. Субъективные характеристики звука применяются для описания музыкальных звуков. Важнейшими из них являются высота тона и тембр.

а. Высота тона звука соответствует частоте колебаний частиц в звуковой волне n. Чем больше n, тем выше тон, и наоборот. Высота тона в музыке описывается нотами. В России принята частотная шкала нот, введенная Международным конгрессом в 1939г.

Приведем в качестве примера частоты, соответствующие нотам первой октавы.

до ре ми фа соль ля си

261,6 293,7 329,6 349,2 392,0 440,0 493,9

Обычно любой стандарт задает лишь значение частоты одной ноты. В данном случае это нота Ля, ее частота принята равной 440 Гц точно. Все остальные ноты "получают" свои частоты с помощью определенных соотношений.

б. Тембр, иначе, окраска звука. Различают чистый тон, музыкальные звуки и шумы.

Чистый тон соответствует звуковой волне, частицы среды в которой колеблются строго по гармоническому закону (рис.119-a).

Музыкальный звук есть сумма нескольких чистых тонов различных интенсивностей (рис.119-б). Тон самой низкой частоты определяет общую высоту звука, более высокие тоны (обертоны) определяют окраску звука, или, иначе, тембр. Частицы среды в музыкальном звуке совершают сложные периодические колебания.

Шум – немузыкальный звук. Частицы среды при шуме совершают непериодические колебания (рис.119-в и 119-г).

в. Громкость подобно уровню интенсивности определяется логарифмом отношения звукового давления к стандартному пороговому звуковому давлению. Если сравнить логарифм отношения давлений с логарифмом отношения интенсивностей, то оказывается, что:

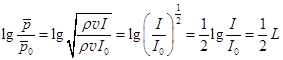. (32.9)

Это значит, что 13 белам уровня интенсивности слышимого диапазона соответствует в два раза меньшее количество единиц громкости, т.е. 13/2 = 6,5. Чтобы привести в соответствие число единиц уровня интенсивности (число децибел) с числом единиц громкости, громкость определяют выражением: 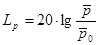. (32.10)

В этом случае шкала громкости практически совпадает со шкалой уровня интенсивности. Единица громкости – фон – равняется децибелу. Поэтому громкость определяют часто как уровень интенсивности и выражают в децибелах.

6. Спектральный анализ звука. Как уже говорилось, любой музыкальный звук есть сумма чистых тонов. Поэтому можно поставить задачу: определить, из каких чистых тонов состоит данный звук. Эта задача решается в рамках спектрального анализа звука. Есть два пути – теоретический и практический.

В основе теоретического метода лежит теорема, сформулированная в 1822г. французским ученым Жаном Фурье (I768–I830) и утверждающая, что любую сложную периодическую функцию можно представить как сумму простых гармонических. Зная кинематический закон сложного периодического движения частиц среды в звуковой волне с помощью математических методов можно определить частоты простых тонов и соответствующие им амплитуды.

Практический путь состоит в том, что изготовляются устройства, в каждом из которых звук возбуждает чистый тон определенной частоты. Если имеется набор таких устройств (их называют резонаторами) с разными частотами собственных тонов, то процедура анализа сводится к выяснению: в которых резонаторах возбуждается звук и какой громкости. По номеру резонатора определяется частота чистого тона, а по громкости – соответствующая этому тону амплитуда колебания частиц.

На графике спектр звука представляют обычно в декартовых координатах, где по оси абсцисс откладывается частота простых тонов, а по оси ординат – их амплитуда (рис.120).

Примером устройств для спектрального анализа звука являются акустические резонаторы Геймгольца (рис.121).