Задача Кеплера. Космические скорости.
1.Поле шаровых однородных тел. Закон всемирного тяготения сформулирован, строго говоря, для точечных масс. Но реальные тела, особенно, космические объекты – Солнце, Земля и другие планеты – имеют весьма протяжённые размеры. Поэтому первая задача, которую Ньютон поставил в теории тяготения, сводилась к вопросу: как взаимодействуют протяженные шаровые тела на малых расстояниях между собой?
Теоретическое решение задачи дало ответ: шаровые однородные тела взаимодействуют так, как если бы вся их масса была сосредоточена в их геометрическом центре. Иначе: гравитационное поле однородного шарового тела массой М такое же, как и поле точечной массы М. Значит, гравитационное поле Солнца, Земли и других планет на расстоянии, большем их радиуса, такое же, как поле соответствующих точечных масс, находящихся в геометрических центрах этих планет. Поэтому напряженность и потенциал поля Земли и других шаровых однородных тел определяются формулами:
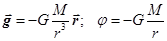 . (14.1)
. (14.1)
при условии r ³ R, где R – радиус Земли или другого шарового тела.
2. Задача Кеплера. Поставим вопрос: при каких условиях и по какой траектории будут двигаться тела в поле тяготения Земли или какой-либо другой планеты?
Обобщенная формулировка этого вопроса о движениb тел в центрально – симметричных полях, создаваемых телами конечных масс, называется в механике задачей Кеплера. Рассмотрим путь её решения при условии, что центральное тело имеет массу, много большую массы движущегося вокруг него тела. Это позволяет считать центральное тело неподвижным.
Силы тяготения – это консервативные и центральные силы. При движении тел в центральном поле тяготения (например, Земли), должны выполняться законы сохранения энергии (система консервативна) и сохранения момента импульса (силы центральные).
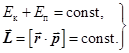 (14.2)
(14.2)
В общем случае два гравитирующих тела движутся относительно общего центра масс. Но наше допущение M>>m позволяет считать центральное тело неподвижным.
Чтобы найти уравнение траектории движения тела m, запишем законы сохранения через координаты и скорости. Так как Eк= 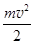 , а Eп=
, а Eп= 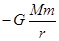 , то
, то 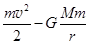 =const. (14.3)
=const. (14.3)
Закон сохранения момента импульса запишем в проекции на ось вращения:  const. (14.4)
const. (14.4)
Итак: 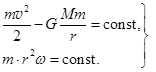 (14.5)
(14.5)
Воспользовавшись полярной системой координат и представив скорости v и w через производные полярного радиуса и полярного угла, 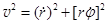 , (14.6)
, (14.6)
где 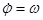 , получаем систему двух дифференциальных уравнений, решение которой дает уравнение траектории в полярных координатах. r = r0
, получаем систему двух дифференциальных уравнений, решение которой дает уравнение траектории в полярных координатах. r = r0 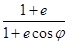 . (14.7)
. (14.7)
 Это уравнение кривой 2-го порядка.
Это уравнение кривой 2-го порядка.
Величину e называют эксцентриси-тетом кривой, e = 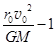 . (14.8)
. (14.8)
Она находится из начальных условий.
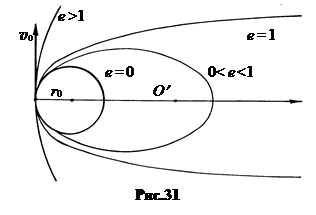
В зависимости от значения эксцентриси-тета траекторией может быть (рис.31):
e = 0 – окружность,
0< e <1 – эллипс,
е = 1 – парабола,
е >1 – гипербола.
Как видно из выражения эксцентриситета е, его значение в поле определенной планеты определяется начальным расстоянием до центра планеты r0 и начальной скоростью движения тела v0.
Круговая скорость тела находится из условия:
| Таблица 2 | |||
| Планета | Круговая скорость, км/с | ||
| h = 0 | h=1000 км | h=5000 км | |
| Меркурий Венера Земля Луна Марс Юпитер Сатурн Уран Нептун | 2,94 7,24 7,91 1,68 3,60 42,60 25,65 15,10 16,55 | 2,48 6,70 7,35 1,34 3,15 42,30 25,45 14,80 16,20 | 1,70 5,38 5,92 0,85 2,27 41,10 24,60 13,80 15,10 |
e = 0, 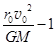 = 0. Þ v0к =
= 0. Þ v0к = 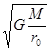 . (14.9)
. (14.9)
В космонавтике круговая скорость называется 1-й космической скоростью. Она зависит от массы планеты и высоты траектории над её поверхностью (табл.2).
В общем случае, начальная скорость, при которой формируется та или иная траектория, определяется из выражения для эксцентриситета.
При е = 1 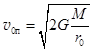 . (14.10)
. (14.10)
Это параболическая скорость. В космонавтике её называют 2-й космической скоростью.
При достижении телом 1-й космической скорости тело будет двигаться по круговой орбите вокруг планеты. Однако, рано или поздно в результате торможения атмосферой планеты и приливными силами тело упадет на поверхность планеты (если она, поверхность, есть).
При достижении телом 2-й космической скорости оно навсегда уходит за пределы тяготения планеты.
3. Упрощённый вывод формул для космических скоростей можно сделать, опираясь на следующие соображения.
Для движения тела по круговой орбите нужно, чтобы центростремительная сила, удерживающая тело на окружности, была равной силе тяготения, то есть 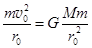 . Отсюда найдется круговая, или 1-я космическая скорость как (14.9).
. Отсюда найдется круговая, или 1-я космическая скорость как (14.9).
При движении тела по параболической траектории механическая энергия тела как на бесконечном удалении от планеты, так и в любой точке траектории равна нулю 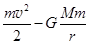 = 0. Отсюда, при r = r0 как (14.10) v =
= 0. Отсюда, при r = r0 как (14.10) v = 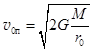 .
.
При движении по окружности или эллипсу тело не может покинуть планету. Такое движение называют ограниченным или финитным.
При движении по параболе или гиперболе тело покидает планету. Это неограниченное, или инфинитное движение.
4. Чёрные дыры. В 1796 г. французский математик Пьер Лаплас, полагая, что свет состоит из частиц, подставил в формулу параболической скорости скорость света, то есть положил, что v0п = c. Это позволило ему придти к важному предсказанию. Если, предположил он, масса гравитирущего тела заключена в шаре с радиусом r0 £ 2G  , то лучи света не смогут покинуть поверхность этого тела. Поэтому для внешнего наблюдателя такое тело, даже будучи нагретым до высокой температуры, остается невидимым. Лаплас, таким образом, предсказал возможность существования так называемых чёрных дыр.
, то лучи света не смогут покинуть поверхность этого тела. Поэтому для внешнего наблюдателя такое тело, даже будучи нагретым до высокой температуры, остается невидимым. Лаплас, таким образом, предсказал возможность существования так называемых чёрных дыр.
Величина 2G  =r0G называется гравитационным радиусом. Для Солнца r0G=3 км, для Земли – 4 мм. Интересно, что строгий вывод в рамках Общей теории относительности даёт для гравитационного радиуса то же самое выражение.
=r0G называется гравитационным радиусом. Для Солнца r0G=3 км, для Земли – 4 мм. Интересно, что строгий вывод в рамках Общей теории относительности даёт для гравитационного радиуса то же самое выражение.
Исследования в теории строения вещества за последние полвека показали, что если Звезда имеет массу в 2 – 3 раза больше солнечной, то в процессе остывания гравитационные силы могут сжать её внутрь гравитационного радиуса. Поэтому вероятность существования во Вселенной таких объектов, как черная дыра, достаточно велика.
Дата добавления: 2020-05-20; просмотров: 906;











