Движение материальной точки под действием упругой силы, силы вязкого сопротивления среды и вынуждающей периодической силы

1.Вынужденные колебания. Это колебания, которые тело совершает при действии на него трёх сил: квазиупругой – kx, вязкого трения – hv_x и гармонической F_x = F₀cos W t, где F₀ – амплитудное значение действующей силы, W – её частота.

Уравнение движения тела имеет вид: m 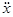= – kx – h 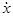+ F₀cos W t. (12.1)

Разделив всё на m и обозначив 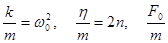= q, получаем:

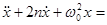qcos W t. (12.2)

Решение этого уравнения состоит из двух частей. Его первое слагаемое представляет собой общее решения уравнения (12.2) без правой части, которое описывает затухающие колебания системы в виде (11.3). Второе слагаемое, как частное решение неоднородного уравнения (12.2), описывает процесс установления вынужденных колебаний с частотой W .

x = Ae^–ntcos( 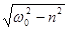t + j₀₁) + В(1 - e^−nt)cos(W t + j₀₂). (12.3)

Спустя время t >>t собственные колебания затухают, и первое слагаемое устремляется к нулю, а второе слагаемое выходит на стационарный режим x = Bcos(W t + j₀). (12.4)

Здесь амплитуда B = 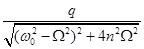, (12.5)

а сдвиг по фазе j₀определяется из формулы: tgj₀ =- 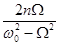. (12.6)

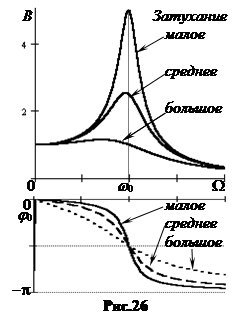2. Резонанс. Амплитуда вынужденных установившихся колебаний при t >>t не зависит от времени и пропорциональна амплитуде вынуждающей силы F₀ (рис.26). Если исследовать функцию B(W) на экстремум, то можно найти значение W_p, при котором амплитуда вынужденных колебаний максимальна.

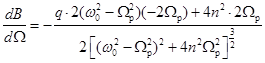= 0, Þ

– w₀² + W_p² + 2n² = 0. (12.7)

Или W_p = 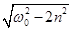. (12.8)

Максимальная амплитуда B_рез = B(W_p) = 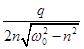. (12.9)

Явление резкого возрастания амплитуды вынужденных колебаний, когда частота вынуждающей силы приближается к частоте 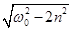(при малом затухании это близко к частоте собственных колебаний) называется резонансом.

При малом затухании, когда n ® 0, B_p ® ¥, упругие деформации могут превысить допустимые и колебательная система разрушается.

При резонансе вынуждающая сила совершает максимальную работу по преодолению сил вязкого сопротивления среды. Когда резонансная амплитуда стабилизируется, работа вынуждающей силы полностью идёт на преодоление сил трения, механическая энергия системы остается постоянной.

При частоте вынуждающих колебаний много меньше собственной амплитуда вынужденных колебаний равна величине упругой деформации под действием амплитудной внешней силы F₀ , колебания совпадают по фазе, сдвиг фаз между ними j₀ = 0.

При частоте вынуждающих колебаний много больше собственной амплитуда вынужденных колебаний стремится к нулевой величине, колебания происходят в противофазе, сдвиг фаз между ними j₀ = p.

При частоте вынуждающих колебаний равной собственной (вблизи резонанса) вынужденные колебания отстают от вынуждающих на четверть периода, j₀ = - p| 2.

3. Линейные и нелинейные колебательные системы. Если параметры колебательной системы – масса тела m, жёсткость пружины k, длина нити l и т.д. – остаются неизменными в процессе колебаний, сила трения линейно зависит от скорости, и квазиупругие силы линейно пропорциональны величине смещения, то колебательная система называется линейной, а колебания описываются линейными дифференциальными уравнениями. Строго говоря, линейные колебательные системы – это идеализация. В реальных колебательных системах силы достаточно сложно (не линейно) зависят от кинематических характеристик – смещения x и скорости v. Такие системы называются нелинейными. Однако, если эти зависимости выражены слабо, то в таких случаях реальная система приближённо может рассматриваться как линейная.

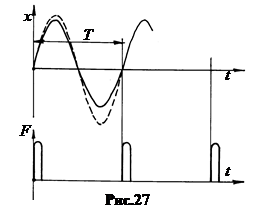4. Автоколебания. В практике для возбуждения колебаний чаще применяется не гармоническая вынуждающая сила, а импульсная, действующая строго периодически в одной и той же фазе (рис.27). Работа этой силы при каждом её действии компенсирует потери энергии колебательной системы на трение в течение каждого периода действия силы.

Такие колебания, строго говоря, не являются гармоническими, но обладают постоянными периодом и амплитудой. Это - автоколебания, а системы, в которых они возникают, называются автоколебательными. Например, часы, свисток, качели, язычковые и духовые музыкальные инструменты.

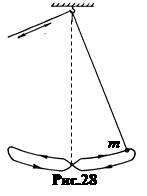5. Параметрическое возбуждение колебаний. Введение энергии в колебательную систему может осуществляться не только путём периодической силы, действующей на тело в направлении его движения, но и путём изменения одного из параметров колебательной системы. Так, если у математического маятника в фазах амплитудных отклонений удлинять нить, а в момент прохождения нити положения равновесия укорачивать её, то колебания будут периодическими и не затухающими (рис.28). Это параметрическое возбуждение колебаний.

Поскольку частота изменения параметра должна быть кратной частоте колебаний, то в параметрическом возбуждении колебаний есть сходство с резонансом, поэтому его называют часто параметрическим резонансом. Сама колебательная система является в этом случае нелинейной.