Неинерциальные системы отсчета (НИСО). Силы инерции

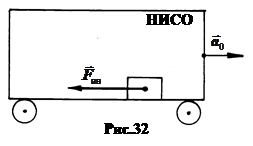1. Поступательно движущаяся НИСО. Наряду с инерциальными системами отсчёта, в которых выполняется первый закон Ньютона, могут существовать системы, в которых этот закон не выполняется. Это системы, движущиеся с ускорением. Их называют неинерциальными.

На тело m, находящееся в системе, движущейся поступательно с ускорением 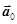, действует в противоположном ускорению направлении сила инерции 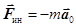(рис.32).

Если составляется уравнение движения тела m относительно НИСО, то в правой части помимо обычных сил – трения, упругости, гравитации и других – добавляется еще и сила инерции. 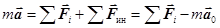. (15.1)

Здесь 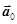– ускорение, испытываемое НИСО.

2. Поступательно и вращательно движущаяся НИСО. Если система отсчета не только движется поступательно с ускорением 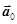, но ещё и вращается с угловой скоростью 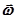и угловым ускорением 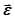(4.9), а тело двигается относительно неё со скоростью 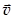, то

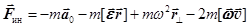. (15.2)

Здесь 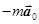– сила инерции, обусловленная неравномерностью поступательного движения НИСО,

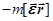– сила инерции, обусловленная неравномерностью вращения НИСО,

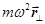– центробежная сила инерции. Она обусловлена самим фактом вращения системы. Символ 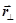означает радиус – вектор, перпендикулярный оси вращения и проведённый от оси к материальной точке m.

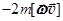– сила инерции Кориолиса. Здесь 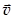– скорость движения точки m относительно НИСО. Сила Кориолиса обусловлена одновременным действием фактов вращения системы и движения тела относительно системы.

Она может обращаться в нуль в 3-х случаях:

НИСО не вращается, 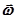= 0.

Тело m покоится относительно НИСО, 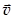= 0.

Тело движется по прямой, параллельной оси вращения НИСО. В этом случае 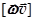=0