Решение задач в ИСО.
 Пример 15.1. Шарик m с помощью нити длиной l закреплен на стержне вращающегося с угловой скоростью
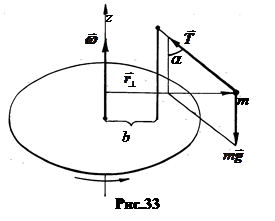
Пример 15.1. Шарик m с помощью нити длиной l закреплен на стержне вращающегося с угловой скоростью 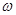 диска (рис.33). Найти угол отклонения нити a и силу натяжения нити Т.
диска (рис.33). Найти угол отклонения нити a и силу натяжения нити Т.
Рассматривая движение в ИСО, мы оперируем только реальными силами. На шарик в ИСО действуют только две силы: сила тяжести 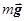 и сила натяжения нити
и сила натяжения нити 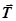 . Под действием этих сил шарик движется по окружности радиуса
. Под действием этих сил шарик движется по окружности радиуса 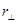 = b + lsina. Уравнение движения шарика имеет вид:
= b + lsina. Уравнение движения шарика имеет вид:
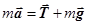 . (15.3)
. (15.3)
Спроектировав это уравнение на ось вращения и радиус вращения, и дополнив систему уравнений кинематическим выражением центростремительного ускорения 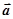 , получаем систему из трёх уравнений с тремя неизвестными a, a, T.
, получаем систему из трёх уравнений с тремя неизвестными a, a, T.
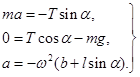 (15.4)
(15.4)
Уравнения линейные, независимые, их число совпадает с числом неизвестных величин, поэтому система имеет единственное решение.
4. Решение задач в НИСО. Если рассматривать движение в НИСО, то в уравнение движения наряду с реальными силами добавляются силы инерции. Полагаем систему отсчета жестко связанной с диском. В этом случае при установившемся постоянном вращении шарик находится относительно системы отсчета в покое, так что 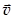 = 0 (рис.34). Уравнение движения в НИСО принимает вид:
= 0 (рис.34). Уравнение движения в НИСО принимает вид: 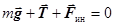 . (15.5)
. (15.5)
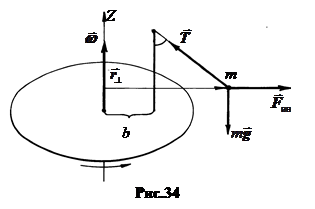 Из всех сил инерции отлична от нуля только центробежная сила,
Из всех сил инерции отлична от нуля только центробежная сила,
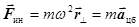 .
.
Спроектировав уравнение движения на радиус вращения и на ось вращения, и добавив выражение для ускорения инерции, получаем систему из трех уравнений.
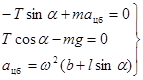 (15.6)
(15.6)
Система содержит 3 неизвестных величины – aцб, a, T – и имеет единственное решение. Полученная система уравнений равносильна системе, к которой мы пришли, решая задачу в ИСО. Таким образом, независимо от того, в какой системе отсчета рассматривается движение, решение задачи должно быть одним и тем же. Характер физического явления не зависит от способа его описания. (Очевидно, 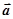 цб = –
цб = – 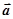 , где
, где 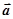 – центростремительное ускорение. Ускорение
– центростремительное ускорение. Ускорение 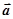 цб есть в НИСО, а центростремительное ускорение
цб есть в НИСО, а центростремительное ускорение 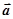 – только в ИСО).
– только в ИСО).
Дата добавления: 2020-05-20; просмотров: 879;











