Понятие о степени реакции
.
Возьмем некоторую к-ю турбинную ступень у которой:
Ро – давление пара перед ступенью;
to – температура пара перед ступенью;
С2(к-1) – скорость пара на входе в направляющий аппарат;
Рd – давление за направляющим аппаратом;
Р1 – давление за ступенью.
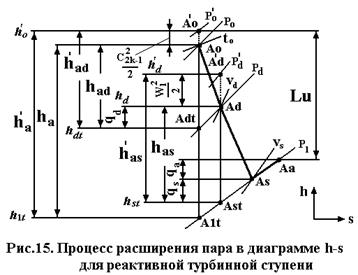
Обратимся к диаграмме h-s (рис.15.). На пересечении изобары Ро и изотермы to находим точку Ао, определяющую состояние пара перед ступенью. Если бы процесс течения пара через ступень происходил без трения, то он изобразился адиабатой АоАdtА1t. Разность энтальпий в точках Ао и А1t определит адиабатный теплоперепад на турбинную ступень:
ha=ho–h1t (3.31)
 Адиабатный теплоперепад на ступень ha характеризует запас потенциальной энергии пара, который может быть преобразован в данной ступени в полезную работу. Кроме того, на входе в ступень пар уже обладает запасом кинетической энергии
Адиабатный теплоперепад на ступень ha характеризует запас потенциальной энергии пара, который может быть преобразован в данной ступени в полезную работу. Кроме того, на входе в ступень пар уже обладает запасом кинетической энергии 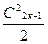 .
.
Таким образом, полный запас энергии, который может быть преобразован в данной ступени в полезную работу, определится суммой адиабатного теплоперепада и входной кинетической энергии пара.
Эта сумма называется располагаемым адиабатным теплоперепадом на ступень:
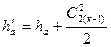 (3.32)
(3.32)
Работа на окружности (полезная работа совершаемая турбинной ступенью), обозначаемая символом Lи, может быть рассчитана как разность располагаемой энергии 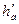 и потерь энергии в турбинной ступени. Для подсчета потерь рассмотрим процесс течения в направляющем аппарате и на рабочих лопатках турбинной ступени.
и потерь энергии в турбинной ступени. Для подсчета потерь рассмотрим процесс течения в направляющем аппарате и на рабочих лопатках турбинной ступени.
Точка Аdt характеризует состояние пара в конце адиабатного расширения в направляющем аппарате. Таким образом, можно определить адиабатные теплоперепады 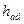 и
и 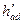 .
.
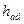 =ho-hdt (3.33)
=ho-hdt (3.33)
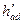 =
= 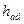 +
+ 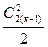 (3.34)
(3.34)
Однако, при течении пара через направляющий аппарат ступени наблюдаются потери энергии qd; за счет этих потерь энтальпия пара за направляющим аппаратом увеличивается и составляет
hd=qd+hdt (3.35)
На пересечении изобары Рd и линии h=const найдется точка Аd, характеризующая действительное состояние пара; процесс в направляющем аппарате изобразится отрезком политропы АоАd.
Далее пар поступает на рабочие лопатки ступени. Если бы процесс на рабочих лопатках происходил без потерь, он изобразился бы отрезком адиабаты АdАst. Таким образом, адиабатный теплоперепад на рабочих лопатках has составит:
has=hd -hst (3.36)
Однако, на рабочих лопатках наблюдаются потери энергии qs; за счет этих потерь энтальпия пара за рабочими лопатками увеличивается и составляет
hs=hst+qs (3.37)
На пересечении изобары Р1 и линии hs = const найдется точка Аs, характеризующая действительное состояние пара; процесс на рабочих лопатках изобразится отрезком политропы АdАs.
На входе из ступени пар имеет «абсолютную» скорость. Таким образом, покидая ступень, пар уносит с собой кинетическую энергию 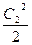 . Эта энергия не может быть преобразована в полезную работу в данной ступени и поэтому для данной ступени она потеряна. Энергия
. Эта энергия не может быть преобразована в полезную работу в данной ступени и поэтому для данной ступени она потеряна. Энергия 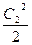 называется потерей с выходной скоростью или просто выходной потерей:
называется потерей с выходной скоростью или просто выходной потерей:
qa= 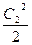 (3.38)
(3.38)
Выйдя из ступени со скоростью С2, поток пара либо плавно войдет в направляющий аппарат следующей ступени, либо просто будет заторможен; для рассматриваемой ступени дальнейшая судьба пара безразлична. Поэтому будем считать, что происходит торможение пара при постоянном давлении Р1, за счет чего энтальпия пара увеличивается. Таким образом, энтальпия пара за ступенью составит
ha=hs+qa (3.39)
Точка Аd, характеризующая состояние пара за ступенью, найдется на пересечении изобары Р1 и линии hа=const. Отрезок изобары АsАa, характеризует торможение пара за ступенью.
Итак, мы установили, что процесс преобразования энергии в ступени сопровождается следующими потерями энергии:
– потери в направляющем аппарате qd;
– потери на рабочих лопатках qs;
– потери с выходной скоростью qa.
Эти потери называются потерями на окружности турбинной ступени.
Тогда работа на окружности Lu может быть определена как разность между располагаемой энергией и потерями на окружности:
Lu=h'а–(qd+qs+qa) (3.40)
Иногда входная энергия 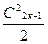 пренебрежительно мала, тогда hа≈ h'а и потому
пренебрежительно мала, тогда hа≈ h'а и потому
Lu=hа–(qd+qs+qa) (3.41)
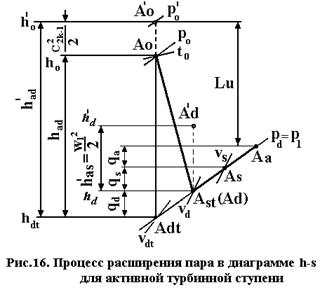 Подсчитанная по формуле (3.40 и 3.41) может быть показана непосредственно на диаграмме h-s (рис.15, 16 и 17).
Подсчитанная по формуле (3.40 и 3.41) может быть показана непосредственно на диаграмме h-s (рис.15, 16 и 17).
Из рассмотренного в диаграмме h-s процесса (рис.15) вытекает, что часть hаd общего теплоперепада на ступень hа срабатывается в направляющем аппарате, а часть hаs – в рабочих лопатках. Для оценки распределение теплоперепадов по венцам вводится понятие степени реакции ступени.
Степенью реакции ρ условимся определять отношением теплоперепада hаs на рабочих лопатках к сумме теплоперепадов на направляющем hаd и рабочем hаs венцах:
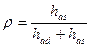 (3.42)
(3.42)
Теперь можно дать более строгие определения введенных ранее понятий активной и реактивной ступеней.
Если ρ=0, а следовательно, hаs=0, то ступень называется активной турбинной ступенью (процесс расширения пара в диаграмме h-s показан на рис.16, где изобара Рd совпадает с изобарой Р1 и теплоперепад hаs станет равным нулю).
 Если ρ≈ 0,5, а следовательно, hаs=hаd, то ступень называется реактивной турбинной ступенью (процесс расширения пара в диаграмме h-s показан на рис.15).
Если ρ≈ 0,5, а следовательно, hаs=hаd, то ступень называется реактивной турбинной ступенью (процесс расширения пара в диаграмме h-s показан на рис.15).
В настоящее время часто применяются ступени, у которых 0<ρ<0,5, а следовательно, 0<hаs<hаd. Такие ступени называются активными турбинными ступенями, с некоторой степенью реакции (процесс расширения пара в диаграмме h-s показан на рис.17).
Соотношение (3.42) определяющее степень реакции часто используют для определения теплоперепадов на венцах. Заметим, что сумма (hаd+hаs) близка к общему теплоперепаду на ступень hа, тогда для адиабатного теплоперепада направляющего аппарата hаd получим:
hаd =(1–ρ)·hа (3.43)
Для адиабатного теплоперепада рабочих лопаток hаs получим:
hаs=ρ·hа (3.44)
2.Форма каналов турбинной решетки. Критические параметры газа, поэтому скорость распространения звука в газе примерна, равна скорости теплового движения молекул (скорость звука при нормальных условиях равна 331 м/с).
Характер течения пара пара.
Ранее установили, что в направляющем аппарате и рабочих лопатках происходит преобразование энергии пара. Возникает вопрос, как при этом изменяются параметры пара, какую должны иметь форму каналы турбинных решеток?
В качестве масштабной величины скорости патока пара принимается скорость звука. Скорость звука – это скорость распространения малых возмущений в среде, например, скорость распространения изменения давления. Процесс распространения сжатия или расширения в газе происходит в результате столкновения молекул в каналах существенно зависит от соотношения скорости течения и скорости звука. Как известно, величина местной скорости звука определяется выражением:
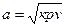 (3.45)
(3.45)
где р, v – давление и удельный объем пара в данном сечении потока;
к – показатель адиабаты.
Для перегретого пара к=1,3. Для насыщенного и влажного пара величина к приближенно может быть оценена по формуле:
к=1,035+0,1·х, (3.46)
где х – степень сухости пара.
При движении парового потока по сопловому каналу давления и температура пара уменьшаются, уменьшается и скорость звука, а скорость потока пара возрастает.
 Если скорость течения пара меньше скорости звука (С<а), но для ускорения потока каналы решетки должны иметь сходящуюся форму. В этом случае скорость течения пара называют дозвуковой, а режим течения – докритическим.
Если скорость течения пара меньше скорости звука (С<а), но для ускорения потока каналы решетки должны иметь сходящуюся форму. В этом случае скорость течения пара называют дозвуковой, а режим течения – докритическим.
Если скорость течения пара больше скорости звука (С>а), то ускорение потока происходит в каналах расходящейся формы. В этом случае говорят о сверхзвуковой скорости пара и сверхкритическом режиме течения.
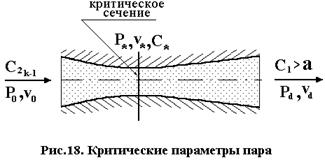
Совершенно очевидно, что для получения сверхзвуковых скоростей на выходе из решетки её каналы вначале должны быть сходящимися, а затем – расходящимися (рис.18). В узком сечении канала скорость течения равна местной скорости звука. Это сечение называется критическим. Критическими параметрами пара называют такие параметры пара, при которых скорость парового пара равна местной скорости звука.
Поставим задачу: определить критическое давление пара. Запишем уравнение энергии для входного и критического сечений. Критические параметры будем обозначать индексом «*».
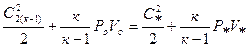 (3.46)
(3.46)
Если ввести в рассмотрение параметры торможения – давление 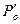 и удельный объем
и удельный объем 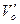 , то левая часть уравнения (2.3.3) запишется в виде:
, то левая часть уравнения (2.3.3) запишется в виде:
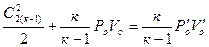 (3.4 7)
(3.4 7)
Запишем, что скорость 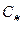 равна местной скорости звука, и потому
равна местной скорости звука, и потому
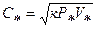
Подставляя значение 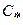
 в (2.3.3), получим:
в (2.3.3), получим:
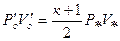 (3.48)
(3.48)
Если предположить, что изменение состояния пара при течении от входного до критического сечений происходит по адиабате, то
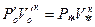
Откуда найдем, что
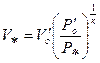
Подставляя значение 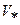 в (.3.48), получим выражение для отношения критического давления
в (.3.48), получим выражение для отношения критического давления 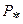 к начальному давлению
к начальному давлению 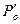 . Это отношение обозначим
. Это отношение обозначим 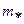 и будем называть критическим отношением давлений:
и будем называть критическим отношением давлений:
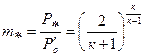 (3.49)
(3.49)
Из (.3.49) видим, что величина критического отношения давлений 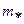 не зависит от величины параметров пара, а зависит только от его физических свойств (природы рабочего тела).
не зависит от величины параметров пара, а зависит только от его физических свойств (природы рабочего тела).
Для перегретого пара 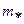 = 0,546. Для насыщенного пара
= 0,546. Для насыщенного пара 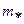 = 0,577.
= 0,577.
Таким образом, зная давление пара перед решеткой и за решеткой, можно сразу решить вопрос о характере течения пара в каналах решетки.
Если 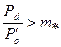 (для рабочей решетки
(для рабочей решетки 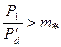 ), то ни в одном из сечений канала не будут достигнуты критические параметры пара; в этом случае скорость пара за решеткой будет дозвуковой, а каналы решетки должны быть сходящимися.
), то ни в одном из сечений канала не будут достигнуты критические параметры пара; в этом случае скорость пара за решеткой будет дозвуковой, а каналы решетки должны быть сходящимися.
Если 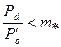 (для рабочей решетки
(для рабочей решетки 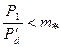 ), то в узком сечении межлопаточных каналов будут достигнуты критические параметры пара, а если за узким сечением имеется расходящаяся часть канала, то за решеткой следует ожидать появления сверхзвуковых скоростей.
), то в узком сечении межлопаточных каналов будут достигнуты критические параметры пара, а если за узким сечением имеется расходящаяся часть канала, то за решеткой следует ожидать появления сверхзвуковых скоростей.
Дата добавления: 2016-06-29; просмотров: 1964;











