Спектральный анализ дискретных сигналов
Вопросы:
1) Дискретные преобразования Фурье реальных сигналов
2) Теорема отсчётов Котельникова
Дискретные преобразования Фурье реальных сигналов
Реальные дискретные сигналы получаются не с помощью дельта импульсов, а с помощью импульсов конкретной формы и конкретной длительности, например прямоугольных.
Спектральная плотность реального дискретного сигнала
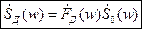
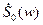 - спектральная плотность импульса дискретизирующей последовательности. Если этот импульс прямоугольный, то спектральная плотность реального дискретного сигнала (из предыдущей лекции) будет
- спектральная плотность импульса дискретизирующей последовательности. Если этот импульс прямоугольный, то спектральная плотность реального дискретного сигнала (из предыдущей лекции) будет
КАРТИНКА
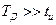
Теорема отсчётов Котельникова
При анализе дискретных сигналов возникает вопрос: каков должен быть период дискретизации, чтобы на приёмной стороне можно было однозначно восстановить исходный непрерывный сигнал. Ответ на этот вопрос даёт теорема Котельникова, сформулированная в 1933 году.
Функцию времени 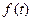 , частотный спектр которой ограничен частотой
, частотный спектр которой ограничен частотой 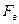 в любой момент времени можно представить в виде ряда
в любой момент времени можно представить в виде ряда
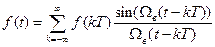 ,
,
где 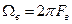
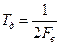
Следствия из теоремы Котельникова:
1) Для того, чтобы можно было однозначно представить аналоговый сигнал дискретным образом, его спектр должен быть ограничен какой-то частотой 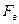 . Теоретически спектр ограниченного по времени сигнала бесконечен по частоте, но практически всегда найдётся частота, за которой спектр можно «обрубить». Например обрывок человеческой речи имеет неограниченный спектр, но никакое ухо не слышит частоты более чем 20 кГц. Поэтому нет смысла передавать весь спектр сигнала. Реальный сигнал всегда ограничен какой-то частотой
. Теоретически спектр ограниченного по времени сигнала бесконечен по частоте, но практически всегда найдётся частота, за которой спектр можно «обрубить». Например обрывок человеческой речи имеет неограниченный спектр, но никакое ухо не слышит частоты более чем 20 кГц. Поэтому нет смысла передавать весь спектр сигнала. Реальный сигнал всегда ограничен какой-то частотой 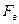 .
.
2) Период дискретизации однозначно определяется этой верхней частотой и должен быть 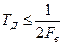
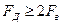
КАРТИНКА
Пусть спектр телефонного сигнала такой. Чтобы из спектра дискретного сигнала оставить спектр исходного непрерывного сигнала, надо пропустить его через фильтр нижних частот. Если частоту дискретизации выбрать неправильно, тогда никаким фильтром нижних частот нельзя выделить спектр исходного непрерывного сигнала.
КАРТИНКА
Цифровые сигналы
Учебные вопросы:
1) Квантование и кодирование
2) Понятие о кодоимпульсной модуляции (КИМ)
Квантование и кодирование
Термин квантование означает деление на порции (кванты). В радиотехнике под квантованием понимают способ задания дискретного сигнала. Различают квантование по времени и по уровню. Квантование по времени можно выполнить, пропустив непрерывный сигнал через быстродействующий ключ.
КАРТИНКА
Квантование по уровню означает задачу сигнала по заданным дискретным уровням. Считается, что сигнал может принимать значения конкретного уровня и никаких промежуточных значений. Очевидно, чем больше уровней, т.е. чем меньше расстояние между ними, тем точнее квантованный сигнал повторяет исходный непрерывный.
Квантованный по уровню сигнал подвергается кодированию. Это означает, что каждому уровню ставится в соответствие цифровой код. Существует множество различных кодов. Широко распространена так называемая КИМ (кодоимпульсная модуляция). Она основана на применении двоичной системы счисления.
КАРТИНКА
| Время | Уровень | Код |
| Т | ||
| 2Т | ||
| 3Т | ||
| 4Т |
Для передачи цифрового сигнала на расстояния без проводов, КИМ сигналом производится амплитудная, частотная или фазовая модуляция радиосигнала.
КАРТИНКА
Если число разрядов равняется n, то количество уровней 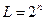 .
.
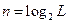
При большом количестве разрядов, а это требуется, когда нужна высокая точность, длительность одного импульса получается очень маленькой, а значит ширина спектра цифрового сигнала большая.
Дата добавления: 2018-11-26; просмотров: 968;











