КАРИТНКИ с фазоимпульсной и частотно-импульсной модуляцией
При фазоимпульсной модуляции меняется местоположение импульса.
При частотно-импульсной модуляции меняется частота следования импульсов.
В радиотехнике для анализа дискретных сигналов часто применяются дискретные преобразования Фурье (ДПФ) и дискретные преобразования Лапласа.
С точки зрения спектрального анализа наиболее удобным является дискретное преобразование Фурье. Для уяснения этого понятия рассмотрим дискретный сигнал 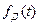 , полученный из непрерывного сигнала
, полученный из непрерывного сигнала 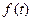 , у которого спектральная плоскость
, у которого спектральная плоскость 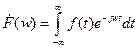 взятием выборок с одинаковым интервалом дискретизации.
взятием выборок с одинаковым интервалом дискретизации.
КАРТИНКА
Сигнал 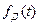 можно получить произведением
можно получить произведением 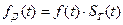
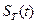 - дискретизирующая последовательность. В данном случае – это последовательность дельта импульсов, следующих на расстоянии
- дискретизирующая последовательность. В данном случае – это последовательность дельта импульсов, следующих на расстоянии 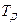
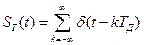
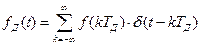
Получим спектральную плотность дискретного сигнала прямым преобразованием Фурье. Обозначим её 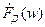
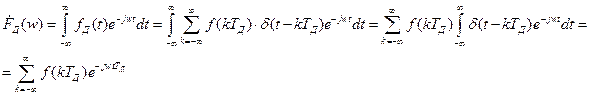
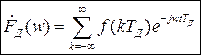 - дискретное преобразование Фурье первой формы.
- дискретное преобразование Фурье первой формы.
С другой стороны дискретизирующая последовательность дельта импульсов представляет собой периодический ряд, и как любой периодический сигнал может быть представлена в виде ряда Фурье.
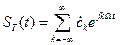
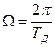
Поскольку спектральная плотность дельта функций равна 1, то 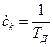
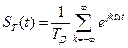
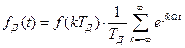
Тогда спектральная плотность данного сигнала 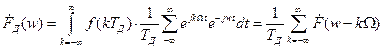
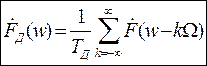 - дискретное преобразование Фурье второй формы.
- дискретное преобразование Фурье второй формы.
КАРТИНКИ
Дискретное преобразование Фурье ещё не даёт спектр реального дискретного сигнала. Оно получено в предположении, что дискретизирующая последовательность – это дельта импульсы. Это идеализированная математическая функция. Но ДПФ помогает отыскать спектр реального сигнала.
Дискретные преобразования Лапласа
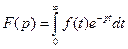 - аналоговое преобразование Лапласа
- аналоговое преобразование Лапласа
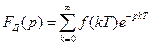 - дискретное преобразование Фурье
- дискретное преобразование Фурье
Решётчатые функции
Из ДПФ и ДПЛ видно, что все операции выполняются над выборками из непрерывных функций. Эти функции называют решётчатыми. Например, решётчатая парабола.
КАРТИНКА
При реализации этих операций в ЭВМ время вообще убирают, остаётся только номер выборки 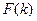 .
.
Дата добавления: 2018-11-26; просмотров: 868;











