Метод комплексных амплитуд
Вопросы:
1) Применение комплексных чисел к анализу и расчету цепей
2) Комплексное сопротивление и комплексная проводимость
3) Уравнения основных элементов при гармонических колебаниях
Анализируя связь между током и напряжением в реактивных элементах ( 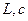 ), замечаем, что уравнения, описывающие такие цепи будут интегральными или дифференциальными. Если цепь сложная, получится система из интегральных и дифференциальных уравнений, решить которую проблематично. Для того чтобы избавится от таких уравнений и применяются символьные или символические методы.
), замечаем, что уравнения, описывающие такие цепи будут интегральными или дифференциальными. Если цепь сложная, получится система из интегральных и дифференциальных уравнений, решить которую проблематично. Для того чтобы избавится от таких уравнений и применяются символьные или символические методы.
В радиотехнике наибольшее распространение используется метод комплексных амплитуд. Сущность любого символического метода заключается в следующем: реальные физические функции времени заменяются их изображениями (некоторой математической функцией (изображением)), затем все операции и расчеты выполняют над изображениями и в конце опять возвращаются к оригиналу (т.е. к реальной функции времени).
Комплексные изображения функций времени
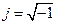
Любое комплексное число, которое имеет вещественную и мнимую часть, можно изобразить на комплексной плоскости следующим образом:
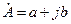
РИСУНОК
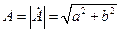
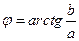 - аргумент комплексного числа
- аргумент комплексного числа
Комплексное число может быть записано так же в показательной форме:
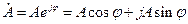
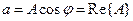
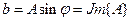
Комплексное представление гармонических функций
Гармонику, например напряжение
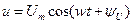
Можно представить в виде комплексного вектора, вращающегося против часовой стрелки с угловой скоростью 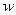 .
.
РИСУНОК
Такое его положение соответствует моменту времени 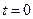 , а угол между вектором и вещественной осью равен начальной фазе.
, а угол между вектором и вещественной осью равен начальной фазе.
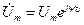
Комплексная амплитуда – это комплексное число, модуль которого равен амплитуде , а аргумент – начальной фазе гармонической функции.
Аналогично
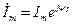
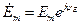
С учетом времени вводят понятие комплексных мгновенных значений
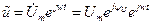
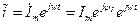
Их можно представить и в алгебраической форме
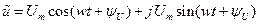
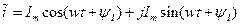
Замечаем, что реальная физическая величина
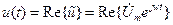
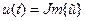
Таким образом, реальным физическим процессам поставлено в соответствие их комплексное изображение
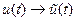
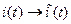
Взяв вещественную и мнимую часть изображений можно вернуться к оригиналу. При анализе линейных цепей оператор вращения можно опустить и работать с комплексными амплитудами, а в конце расчетов его вернуть и получить мгновенное значение.
Если к пассивному линейному двухполюснику приложить гармоническое напряжение 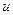 , то возникший ток тоже будет гармоническим. Определим комплексное сопротивление как отношение комплексных амплитуд напряжения и тока
, то возникший ток тоже будет гармоническим. Определим комплексное сопротивление как отношение комплексных амплитуд напряжения и тока
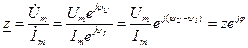
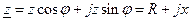
Активное сопротивление влияет на безвозвратные потери мощности в цепи
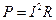
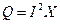 - реактивная мощность, которая запасается в цепи и может возвращаться обратно.
- реактивная мощность, которая запасается в цепи и может возвращаться обратно.
Величина, обратная сопротивлению – комплексная проводимость
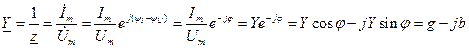
Известные нам законы Ома и Кирхгофа можно записать в комплексной форме
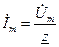
Комплексная форма записи мощности:
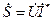
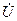 - комплексное действующее значение напряжения
- комплексное действующее значение напряжения
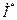 - комплексное действующее сопряжённое значение тока
- комплексное действующее сопряжённое значение тока
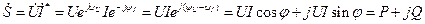
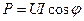 - активная мощность
- активная мощность
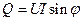 - реактивная мощность
- реактивная мощность
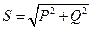 - полная мощность
- полная мощность
Цепь с активным сопротивлением
РИСУНОК
В цепи, состоящей из активного сопротивления приложили гармоническое напряжение
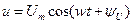
Требуется определить мгновенное значение тока
Переходим в область изображений. Будем оперировать комплексными амплитудами напряжения и тока
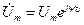
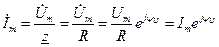
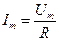
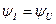
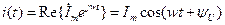
В цепи с активным сопротивлением ток и напряжение совпадают по фазе.
РИСУНОК –векторная диаграмм напряжений и токов
Полная комплексная мощность
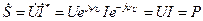
Цепь с индуктивностью
Анализ индуктивности легче начинать, задав ток
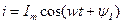
Перейдём к изображению:
РИСУНОК
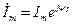
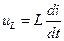
Следовательно
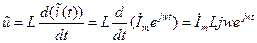
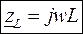
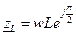
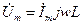
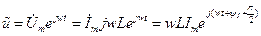 - мгновенное значение тока в индуктивности
- мгновенное значение тока в индуктивности
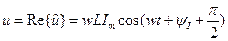
Это позволяет сделать следующие выводы:
В цепи с индуктивностью разность фаз напряжения и тока 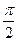 , т.е. напряжение опережает ток на 90 градусов.
, т.е. напряжение опережает ток на 90 градусов.
РИСУНОК
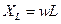
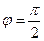
Это означает, что ток, протекающий через индуктивность будет уменьшаться пропорционально частоте.
Мощность
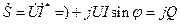 - чисто реактивная мощность.
- чисто реактивная мощность.
Это значит, что в индуктивности энергия не расходуется, а запасается в виде электрического поля и возвращается обратно.
Цепь с емкостью
Если к емкость c приложить напряжение
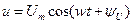
В этом случае потечёт гармонический ток
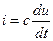
При переходе к комплексным изображениям
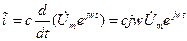
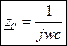 или
или 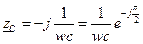
Мгновенное значение тока
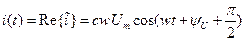
В цепи с емкостью ток впереди напряжения на 90 градусов.
РИСУНОК
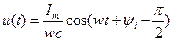
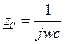
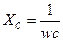
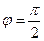
Полная мощность
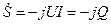 - чисто реактивная мощность
- чисто реактивная мощность
Цепь последовательно соединённых 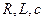
РИСУНОК
При последовательном сопротивлении удобно считать заданным ток
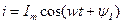
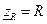
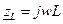
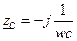
Согласно первому закону Кирхгофа,
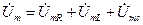
Согласно закону Ома
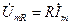
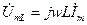
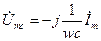
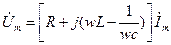
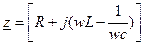
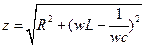
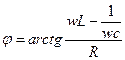
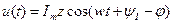
Из полученного выражения пока не очень видны фазовые соотношения между напряжением и током в такой цепи. Пока видно, только что он зависит от частоты. Для того, чтобы выяснить, каким образом  зависит от частоты, изобразим графическую зависимость
зависит от частоты, изобразим графическую зависимость  .
.
РИСУНОК
Частота, на которой
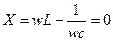 называется резонансной.
называется резонансной.
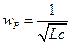
На частотах 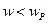 преобладает емкостной характер сопротивления:
преобладает емкостной характер сопротивления:
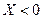 . Следовательно, векторная диаграмма будет выглядеть следующим образом:
. Следовательно, векторная диаграмма будет выглядеть следующим образом:
РИСУНОК
На частотах, меньших резонансной данная цепь имеет активное емкостное сопротивление и может быть заменена такой схемой:
РИСУНОК
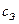 находится из следующих соображений:
находится из следующих соображений:
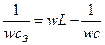
На частотах 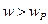 , то преобладает индуктивное сопротивление, т.е.
, то преобладает индуктивное сопротивление, т.е.
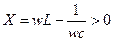 Векторная диаграмма будет такая:
Векторная диаграмма будет такая:
РИСУНОК
На частотах, меньших резонансной данная цепь имеет активное индуктивное сопротивление и может быть заменена такой схемой:
РИСУНОК
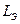 находится из следующих соображений:
находится из следующих соображений:
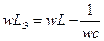
На резонансной частоте
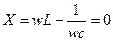 Векторная диаграмма будет такая:
Векторная диаграмма будет такая:
РИСУНОК
На резонансной частоте фаза напряжения равна фазе тока.
В параллельной схеме лучше всего работать с проводимостью.
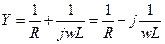
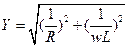
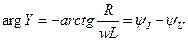
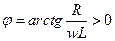
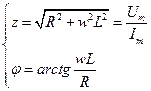
Дата добавления: 2018-11-26; просмотров: 1518;











