Спектральные плотности типовых элементарных сигналов

Учебные вопросы:

1) Прямоугольный импульс.

2) Экспоненциальный импульс

3) Дельта импульс

4) Гауссов импульс

Существуют виды импульсов, наиболее часто применяемые в радиотехнике. Кроме того некоторые из импульсов реально в природе не встречаются, но широко используются для моделирования реальных сигналов.

Прямоугольный импульс

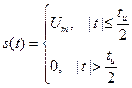
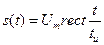
Функция 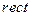обозначает прямоугольный импульс длительностью 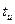, расположенный симметрично относительно начала координат.

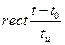- прямоугольный импульс, сдвинутый вправо на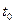

Функция 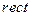безразмерна и равна 1 в пределах длительности.

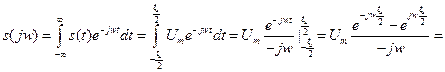
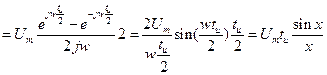- выражение для спектральной плотности прямоугольного импульса

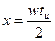
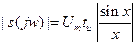
Функция 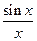обращается в 0 там, где синус равен 0. Т.е. .

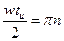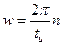
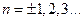
ДВЕ КАРТИНКИ!

Спектральная плотность вещественная, бывает положительной и отрицательной. Аргумент вещественного положительного числа равен 0, аргумент вещественного отрицательного числа равен .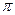

Картинка

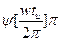
Квадратные скобки означают целую часть.

Ширина спектра такого сигнала, определённая по амплитудному критерию на уровне 0,1

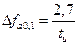
А ширина спектра по энергетическому критерию по уровню 0,9

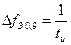
Отсюда следует, что чем уже импульс, тем шире его спектр.

Экспоненциальный импульс

КАРТИНКА

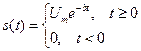
Теоретически, импульс длится до бесконечности, а практически надо как-то сравнивать импульсы разной длительности. Для оценки длительности импульса вводят коэффициент 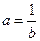[с]. Если на оси времени поставить точку 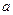и подставить её значение в выражение для импульса, то получим

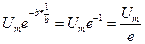
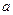- длительность импульса на уровне 0,37 от максимального значения.

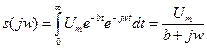
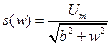- модуль спектральной плотности

КАРТИНКА

Оценим ширину спектра по амплитудному критерию на уровне 0,707 от максимального значения.

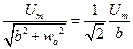
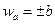
Поскольку отрицательные частоты физического смысла не имеют, то ширина спектра равняется .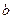

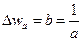
Мы опять получаем утверждение, что чем шире импульс, тем уже его спектр и наоборот.

Произведение длительности импульса на ширину спектра называется базой сигнала.

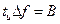
В нашем случае база равна 1.

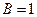
У всех простых сигналов база примерно равна 1.

Аргумент спектральной плотности

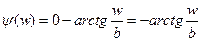
КАРТИНКА

Дельта импульс

Дельта импульс – математическая абстракция. В природе его не существует, но он широко используется ля моделирования реальных сигналов. Дельта импульс должен удовлетворять двум условиям:

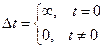
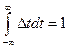
Важнейшее свойства дельта импульса

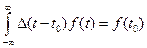- фильтрующее свойство дельта функции

КАРТИНКА

Определим спектральную плотность сдвинутого дельта импульса

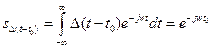
Определим спектральную плотность несдвинутого дельта импульса, подставив вместо 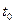0.

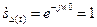
КАРТИНКА

У бесконечно короткого импульса бесконечно широкий спектр.

Гауссов импульс

По другому Гауссов импульс называется колоколообразным.

КАРТИНКА

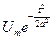
Особенность данного импульса состоит в том, что это единственный в природе сигнал, у которого форма спектральной плотности такая же, как и форма сигнала. У этого сигнала самая маленькая база, которая равняется 0,22, если ширину спектра оценивать по энергетическому критерию на уровне 90%.