РИСУНКИ СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ

Чтобы найти амплитудно-частотный спектр непериодического сигнала необходимо:

1) Выкинуть левую половину из спектральной плоскости.

2) Умножить модуль спектральной плотности на 2 и заштриховать всё под этой линией.

Чтобы получит фазочастотный спектр непериодического сигнала, надо убрать левую часть в аргументе спектральной плотности.

Спектр периодического сигнала тоже можно получить, пользуясь понятием спектральной плотности.

1) Прямым преобразованием Фурье ищем спектральную плотность. Для периодического сигнала такой же формы, как и одиночного импульса, она будет одинаковой.

Например для прямоугольного импульса модуль спектральной плоскости будет таким:

РИСУНОК

2) Стираем левую часть.

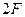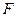3) Умножаем правую часть на , где - частота повторения и расставляем под этой кривой палочки, следующие на расстоянии .

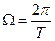Для получения фазочастотного спектра берём аргумент данной плотности, убираем отрицательные частоты расставляем палочки на том же расстоянии .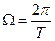

Таким образом спектр периодического сигнала можно получить с помощью ряда Фурье, а можно с помощью спектральной плотности. Спектр же непериодического сигнала можно получить только с помощью спектральной плотности, поскольку в ряд он не рассказывается.

Основные свойства спектральной плотности

Часто в радиотехнике возникает следующая задача: зная спектр одного сигнала, не делая преобразований Фурье, найти спектр другого сигнала, при этом сигналы должны быть связаны друг с другом.

РИСУНОК

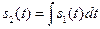
Свойства спектральной плотности:

1) Модуль спектральной плотности – всегда чётная функция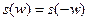

2) Аргумент спектральной плотности – функция нечётная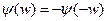

3) Сдвиг сигнала во времени. РИСУНОК!!! 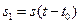. Если сигналу 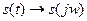, то 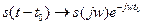, т.е. модуль спектральной плотности не изменится, а начальные фазы получат добавку 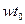, пропорциональную частоте.

4) Изменение масштаба во времени. РИСУНОК!!! 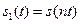. Отсюда получаем , что если 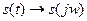, то 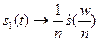. Это фундаментальное положение спектрального анализа сигнала: во сколько раз уменьшится длительность импульса, во столько же раз расширится его спектр, но при этом уменьшатся амплитуды составляющих спектра.

5) Сложение сигналов. Если 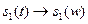, 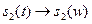то 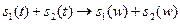. Это правило распространяется на какое угодно количество сигналов.

6) Дифференцирование и интегрирование сигналов. Пусть сигналу 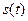соответствует спектральная плотность 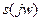. Тогда 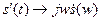. 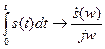за исключением .

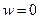7) Спектральная плотность при нулевой частоте. 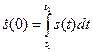- интеграл от сигнала. Т.е. постоянная составляющая – есть площадь сигнала. Однако если сигнал симметричен оси времени, значит постоянной составляющей в нём нет. У любого сигнала. Не симметричного относительно оси времени будет постоянная составляющая.