Преобразования Фурье

В ряд Фурье раскладывается только периодический сигнал. Возникает вопрос как отыскать спектральный состав непериодического сигнала, например одиночного импульса.

Сначала предположим, что это был периодический сигнал с периодом T, т.е. добавим слева и справа бесконечное количество таких же импульсов. Получили периодический сигнал 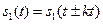. Этот сигнал можно представить в виде ряда Фурье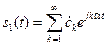

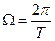- частота повторения

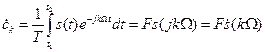
Теперь устремляем период в бесконечность, таким образом периодический сигнал превращаем в одиночный.

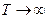
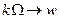- дискретные частоты заменяются непрерывными

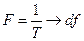
Расстояние между отдельными гармониками спектра становятся бесконечно малыми, а спектр – сплошным. В спектре непериодического сигнала присутствуют колебания всех частот от 0 до .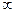

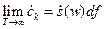
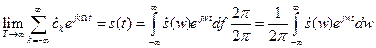
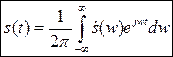- обратное преобразование Фурье.

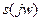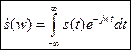Величина или - спектральная плотность сигнала.

Спектральная плотность обладает свойствами коэффициентов 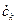комплексного ряда Фурье. Отличается только сомножителем .

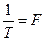Спектральная плотность показывает распределение комплексных амплитуд гармоник в спектре сигнала по частотам.

Спектральная плотность есть некоторая математическая абстракция, поскольку она определена и для отрицательных, и для положительных частот. Т.е. если мы изобразим модуль спектральной плотности, он будет и слева, и справа.

Спектральная плотность может быть применена как к периодическому, так и к непериодическому сигналу. Форма спектральной плотности зависит только от формы сигнала и не зависит от периода. Т.е. у одиночного импульса и периодического импульса (такого же по форме), спектральная плотность будет одинакова. Из определения спектральной плотности видно, что её можно представить в следующей форме .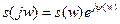

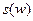- модуль спектральной плотности

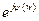- аргумент спектральной плотности

Прямое преобразование Фурье позволяет получить спектральную плотность сигнала зная сам сигнал. Спектральная плотность – это математическая абстракция, но она помогает найти реальный спектр сигнала. Обратное преобразование Фурье помогает найти сигнал, зная его спектральную плотность.