Расчеты сжатого стержня на устойчивость.

Расчет сжатых стержней осуществляется не только на прочность, но и на устойчивость. Рабочее напряжение, которое возникает в поперечном сечении стержня не должно превышать расчетное сопротивление на устойчивость. Это условие математически выражается следующим неравенством:

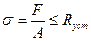(13.18)

Расчетное сопротивление на устойчивость стержня значительно меньше от расчетного сопротивления на прочность, то есть 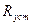< 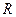. В таком случае можно принять следующую зависимость между расчетными сопротивлениями на устойчивость стержня и на прочность:

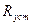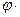
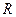= , (13.19)

где 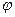- коэффициент уменьшения основного допустимого напряжения при сжатии стержня, который имеет название коэффициента продольного изгиба стержня. Значения этого коэффициента зависят от гибкости стержня и материала, из которого он изготовлен.

Значения коэффициента 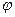приведены в таблице 13.1.

Таблица 13.1

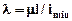
Гибкость	Коэффициенты 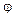для разных материалов
Сталь Ст. 4, 3, 2, ОС	сталь Ст5	сталь СПК	чугун	Древесина
	1,00 0,99 0,96 0,94 0,92 0,89 0,86 0,81 0,75 0,69 0,60 0,52 0,45 0,40 0,36 0,32 0,29 0,26 0,23 0,21 0,19	1,00 0,98 0,95 0,92 0,89 0,86 0,82 0,76 0,70 0,62 0,51 0,43 0,36 0,33 0,29 0,26 0,24 0,21 0,19 0,17 0,16	1,00 0,97 0,95 0,91 0,87 0,83 0,79 0,72 0,65 0,55 0,43 0,35 0,30 0,26 0,23 0,21 0,19 0,17 0,15 0,14 0,13	1,00 0,97 0,91 0,81 0,69 0,57 0,44 0,34 0,26 0,20 0,16 — — — — — — — — — —	1,00 0,99 0,97 0,93 0,87 0,80 0,71 0,60 0,48 0,38 0,31 0,25 0,22 0,18 0,16 0,14 0,12 0,11 0,10 0,09 0,08

После замены в формуле (13.18) расчетного сопротивления на устойчивость 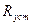расчетным сопротивлением на прочность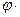 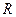получим окончательное условие устойчивости сжатого стержня:

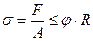(13.20)

Кроме условия устойчивости для сжатого стержня должно выполняться условие прочности:

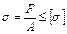(13.21)

Используя условие устойчивости (13.20), можно решать три вида задач:

1) Проверить выполнение условия устойчивости. В случае, если известны сила сжатия F, форма и размеры поперечного сечения, то есть его площадь А, а также расчетное сопротивление и условия закрепления стержня, то достаточно определить гибкость стержня, найти соответствующее значение коэффициента φ, подставить эти значения в условие (13.20) и убедиться, что оно выполняется. Если это условие не выполняется, то нужно уменьшить величину силы, или увеличить размеры сечения и опять проверить выполнение условия устойчивости.

2) Осуществить подбор поперечного сечения стержня, то есть осуществить проектный расчет стержня. В этом случае должны быть известные сила сжатия F, расчетное сопротивление на устойчивость, форма и соотношение размеров поперечного сечения стержня, а также условия закрепления стержня.

Расчет заключается в определении размеров поперечного сечения и выполняется методом последовательных приближений, поскольку гибкость стержня зависит от геометрических характеристик поперечного сечения стержня, которые неизвестны.

Поэтому в первом приближении условно принимается φ = 0,5, определяется требуемая площадь сечения, потом определяются его геометрические характеристики относительно главных центральных осей инерции, находится гибкость и соответствующее ей значение коэффициента φ.

Если это значение значительно отличается от принятого значения φ = 0,5, то выполняется второе приближение, в котором значение φ принимается равным среднему арифметическому двух значений, принятому и полученному в первом приближении. Расчет продолжают до тех пор, пока разница между принятым значением и полученным значением коэффициента φ не станет меньше 5%. В следующем параграфе будет выполнен проектный расчет стержня на устойчивость.

3) Определить допускаемое значение силы сжатия F. Если известны форма и размеры поперечного сечения, его площадь и расчетное сопротивление на устойчивость, то достаточно определить гибкость стержня, найти соответствующее значение коэффициента φ, подставить эти значения в условие (13.20) и определить допускаемую величину действующей силы.