Примеры расчета сжатого стержня на стойкость.
Пример 13.1. Для деревянной колонны высотой 4 м., сжатой силой F = 60 кН и жестко закрепленной внизу (рис.13.3), нужно определить размеры поперечного сечения прямоугольной формы, если стороны прямоугольника соотносятся как 1:2. Условия закрепления колонны одинаковые относительно двух главных осей инерции сечения. расчетное сопротивление древесины на сжатие принять равным 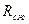 =8 МПа.
=8 МПа.
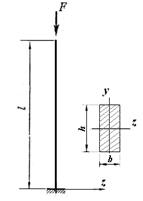
Рис.7.3
Последовательность расчета: 1) Выполняем расчет колонны в первом приближении:
- Расположим прямоугольное сечение колонны так, чтобы ось максимальной инерции z была горизонтальной. В таком случае потеря устойчивости колонны будет происходить в направлении этой оси (то есть изгиб стойки происходит относительно оси y– оси минимальной инерции сечения).
- Принимаем φ= 0,5 и определяем необходимую площадь поперечного сечения колонны из условия устойчивости (13.20)
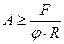 , откуда
, откуда 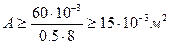 , или
, или 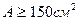
Для прямоугольного сечения со сторонами b и h=2b имеем
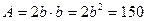 , тогда
, тогда 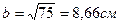 и
и
h=2b=2∙8,66 =17,32 см.
- Определим максимальную гибкость колонны относительно оси yсначала в общем виде, потом при найденном значении b = 8,66 см.
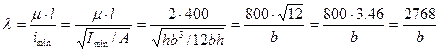
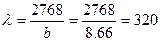
Из таблицы 13.1 находим значение коэффициента φ΄ = 0,08 (для древесины при максимальной гибкости 200). Полученная величина значительно меньше от принятого значения φ = 0,5. Поэтому нужно выполнить перерасчет размеров сечения колонны.
2) Выполняем расчет колонны во втором приближении:
- Принимаем φ = 0,29 (среднее арифметическое двух значений коэффициента φ, принятого и полученного в первом приближении) и определяем необходимую площадь поперечного сечения колонны из условия устойчивости.
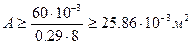 , или
, или 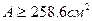
Для прямоугольного сечения со сторонами b и h=2b имеем
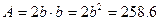 , тогда
, тогда 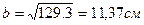 и
и
h=2b=2∙11,37 =22,74 см.
- Определим максимальную гибкость колонны относительно оси y
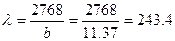
Из таблицы 13.1 находим значение коэффициента φ΄ = 0,08 (для древесины при максимальной гибкости 200). Полученная величина значительно меньше от принятого значения φ = 0,29. Поэтому нужно опять выполнить перерасчет размеров сечения колонны.
3) Выполняем расчет колонны в третьем приближении:
- Принимаем φ = 0,185 (среднее арифметическое двух значений φ, приятого и полученного во втором приближении) и определяем необходимую площадь поперечного сечения колонны из условия устойчивости.
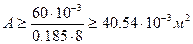 , или
, или 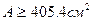
Для прямоугольного разреза со сторонами b и h=2b имеем
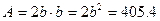 , тогда
, тогда 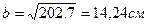 и
и
h=2b=2∙14,24 =28,48 см.
- Определим максимальную гибкость колонны относительно оси y
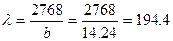
Из таблицы 7.1 находим значение коэффициента φ΄ = 0,086 (для древесины при гибкости 194,4). Полученная величина также меньше от принятого значения φ = 0,185. Поэтому нужно опять выполнить перерасчет размеров сечения колонны.
4) Выполняем расчет колонны в четвертом приближении:
- Принимаем φ = 0,136 (среднее арифметическое двух значений φ, принятого и полученного в третьем приближении) и определяем необходимую площадь поперечного сечения колонны из условия устойчивости.
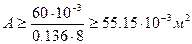 , или
, или 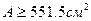
Для прямоугольного разреза со сторонами b и h=2b имеем
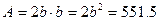 , тогда
, тогда 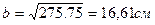 и
и
h=2b=2∙16,61 =33,22 см.
- Определим максимальную гибкость колонны относительно оси y
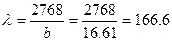
Из таблицы 7.1 находим значение коэффициента φ΄ = 0,113 (для древесины при гибкости 166,6). Полученная величина отличается от принятого значения φ = 0,136 больше чем на 5%. Поэтому нужно опять выполнить перерасчет размеров сечения колонны.
5) Выполняем расчет колонны в пятом приближении:
- Принимаем φ = 0,124 (среднее арифметическое двух значений φ, принятого и полученного в четвертом приближении) и определяем необходимую площадь поперечного сечения колонны из условия устойчивости.
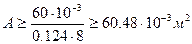 , или
, или 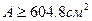
Для прямоугольного разреза со сторонами b и h=2b имеем
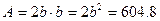 , тогда
, тогда 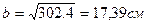 и
и
h=2b=2∙17,39 =34,78 см.
- Определим максимальную гибкость колонны относительно оси y.
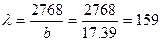
Из таблицы 13.1 находим значение коэффициента φ΄ = 0,122 (для древесины при гибкости 159). Полученная величина отличается от принятого значения φ = 0,124 на 1,63%. Таким образом, расчет можно считать законченным. Остается лишь определить рабочее напряжение в стержне и расчетное сопротивление на устойчивость и сравнить их значения.
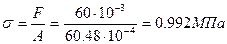 ;
;
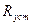 =
= 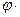
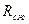 ,
, 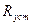 = 0,124∙8 = 0,992 МПа.
= 0,124∙8 = 0,992 МПа.
Таким образом, условие устойчивости выполняется. Рабочее напряжение не превышает расчетного сопротивления.
Пример 13.2. Для колонны высотой 6м, нужно определить размеры поперечного сечения, составленного из двух, объединенных полками равнополочных уголков, если колонна сжата силой F = 250 кН и имеет разные условия закрепления относительно двух главных осей инерции сечения (рис.13.4). Расчетное сопротивление стали на сжатие принять ровным 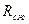 =160 МПа.
=160 МПа.
Последовательность расчета:
1) Выполняем расчет колонны в первом приближении. На рис.13.4,а и 13.4,б показанные коэффициенты приведенной длины стержня относительно главных осей инерции сечения. Расположим сечение колонны так, чтобы центральная ось максимальной инерции сечения (ось z) была перпендикулярной к плоскости с большим коэффициентом приведенной длины (рис.13.4,в).
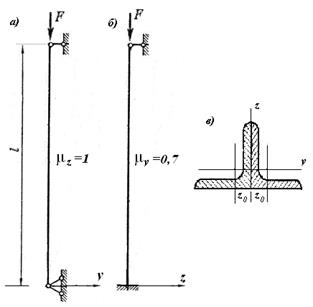
Рис.13.4
Принимаем φ = 0,5 и определяем необходимую площадь поперечного сечения колонны из условия устойчивости (13.20)
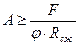 , откуда
, откуда 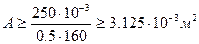 ,
,
или 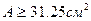
Площадь сечения одного уголка составляет 15,625 см2. Пользуясь таблицей сортамента прокатных профилей уголковой стали, находим равнополочный уголок
№ 10 х 0,8, площадь сечения которого равна: А = 15,6 см2. Из той же таблицы находим значения осевых моментов инерции уголка относительно собственных центральных осей, а также значение координаты центра тяжести уголка:
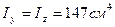 , z0 =2,75 см.
, z0 =2,75 см.
Центр тяжести всего сечения, состоящего из двух уголков, находится на оси симметрии этого сечения на расстоянии
z0 =2,75 см от нижней границы сечения.
Определяем моменты инерции и радиусы инерции сечения колонны относительно главных центральных осей:
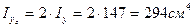 ,
,
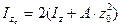 ,
, 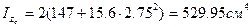
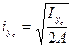 , тогда
, тогда 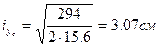 ;
;
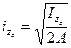 , тогда
, тогда 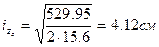
Определим гибкость колонны относительно главных осей инерции сечения:
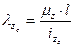 , тогда
, тогда 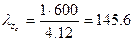 ;
;
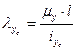 , тогда
, тогда 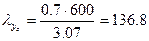
Таким образом, максимальная гибкость имеет место относительно оси zспоперечного сечения колонны и равняется 145,6.
По таблице 13.1 находим значение коэффициента φ΄ = 0,338 (для стали марок: Ст2, Ст3, Ст4 при гибкости 145,6). Полученная величина значительно меньше от принятого значения φ = 0,5. Поэтому нужно выполнить перерасчет размеров сечения колонны. Пересчет выполняем лишь в одной плоскости большей гибкости колонны, то есть в плоскости xOz.
2) Выполняем расчет колонны во втором приближении:
Принимаем φ = 0,419 (среднее арифметическое значение принятого и полученного значения φ в первом приближении) и определяем необходимую площадь поперечного сечения колонны из условия устойчивости.
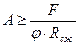 , откуда
, откуда 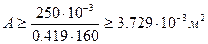 , или
, или 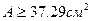
Площадь сечения одного уголка составляет 18,64 см2
Пользуясь таблицами сортамента прокатных профилей уголковой стали находим равнополочный уголок № 10 х 1, для которого:
А = 19,2 см2, 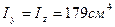 , z0 =2,83 см.
, z0 =2,83 см.
Определяем момент и радиус инерции сечения колонны относительно главной центральной оси zс:
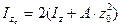 ,
, 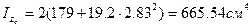
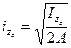 , тогда
, тогда 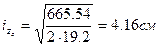
Определим гибкость колонны относительно оси zс:
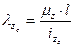 , тогда
, тогда 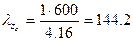 ;
;
По таблице 13.1 находим значение коэффициента φ΄ = 0,343 (для стали марок: Ст2, Ст3, Ст4 при гибкости 144,2). Полученная величина отличается от принятого значения φ = 0,419 больше чем на 5%, а рабочее напряжение превышает расчетное сопротивление на устойчивость. В этом легко убедиться, если определить и сравнить эти напряжения:
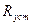 =
= 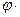
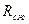 ,
,  = 0,343∙160 =54,88 МПа.
= 0,343∙160 =54,88 МПа.
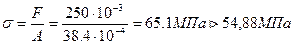
Поэтому нужно опять выполнить перерасчет размеров сечения колонны в одной плоскости большей гибкости, то есть в плоскости xOz.
3) Выполняем расчет колонны в третьем приближении:
Принимаем φ = 0,381 (среднее арифметическое принятого и полученного значения φ во втором приближении) и определяем необходимую площадь поперечного сечения колонны из условия устойчивости:
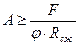 , откуда
, откуда 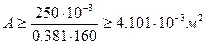 , или
, или
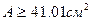
Площадь сечения одного уголка составляет 20,5 см2
Пользуясь таблицами сортамента прокатных профилей стали, находим равнополочный уголок № 12,5 х 0,8 для которого:
А = 19,7 см2, 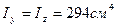 , z0 =3,36 см.
, z0 =3,36 см.
Определяем момент и радиус инерции разреза колонны относительно главной центральной оси zс:
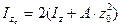 ,
, 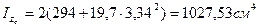
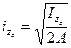 , тогда
, тогда 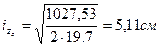
Определим гибкость колонны относительно оси zс:
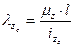 , тогда
, тогда 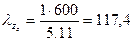 ;
;
Из таблицы 13.1 находим значение коэффициента φ΄ = 0,468 (для стали марок: Ст2, Ст3, Ст4 при гибкости 117,4). Полученная величина отличается от принятого значения φ = 0,419 больше чем на 5%, но в сторону увеличения этого коэффициента. Поэтому расчет завершаем и определяем допускаемое напряжение на устойчивость колонны из двух уголков №12,5х0,8, а также рабочее напряжение в поперечном сечении колонны.
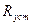 =
= 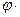
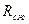
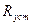 = 0,468∙160 =74,88 МПа.
= 0,468∙160 =74,88 МПа.
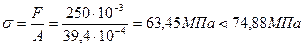 .
.
Сравнивая эти величины, заключаем, что устойчивость колонны принятого поперечного сечения полностью обеспечивается.
Список литературы
1. Беляев Н.М. Сопротивление материалов. Издательство «Наука». М., 1976.
2. Дарков А.В., Шпиро Г.С. Сопротивление материалов. Издательство «Высшая школа». М., 1975.
3. Гастев В.А. Краткий курс сопротивления материалов. Издательство «Наука». М., 1976.
4. Долинский Ф.В., Михайлов М.Н. Краткий курс сопротивления материалов. Издательство «Высшая школа». М., 1988.
5. Писаренко Г.С., Яковлев А.П., Матвеев В.В. Справочник по сопротивлению материалов. Издательство «Наукова думка». Киев, 1975.
6. Писаренко Г.С. Сопротивление материалов. Издательство «Высшая школа». Киев, 1986.
7. Тимошенко С.П. Сопротивление материалов т.1. Элементарная теория и задачи. Издательство «Наука». М., 1965.
8.
Дата добавления: 2018-11-26; просмотров: 1012;











