Определение напряжений в сжатом стержне.

Критическое напряжение, которое возникает в поперечном сечении стержня, равняется отношению критической силы к площади этого сечения, то есть:

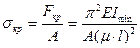(13.12)

Отношение минимального момента инерции поперечного сечения к его площади, есть квадрат минимального радиуса инерции:

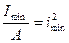
Обозначим через λ отношения приведенной длины стержня к минимальному радиусу инерции поперечного сечения:

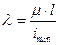(13.13)

Эта величина называется гибкостью стержня и является мерой его устойчивости. Она зависит от формы и размеров поперечного сечения стержня, его длины и условий закрепления. С учетом (13.13) формула (13.12) приводится к виду:

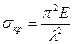(13.14)

По формуле (13.14) можно определять критическое напряжение лишь при условии, что оно не превышает предела пропорциональности, то есть при условии 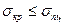, в этом случае гибкость λ принимает предельное значение λ_пр. Используя это условие и формулу (13.14) получим:

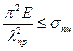, откуда 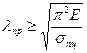(13.15)

Определим, например, предельную гибкость стального стержня. Для малоуглеродистых сталей имеем: E = 2∙10⁵ МПа, и

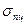= 200 МПа, тогда:

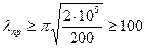
Таким образом, критические напряжения в сжатом стержне, изготовленном из стали, можно определять по формуле (13.14), если предельная гибкость не меньше 100 единиц. (Для деревянного стержня предельная гибкость равняется 110, а для стержня, изготовленного из чугуна – 80).

Если гибкость стержня меньше предельной гибкости, то критические напряжения определяются по эмпирической формуле Ясинского:

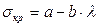(13.16)

Коэффициенты а и b зависят от свойств материала стержня и определяются опытным путем. Например, для малоуглеродистой стали, принимают: а = 310 МПа и b = 1,14 МПа.

Критическая сила в этом случае определяется как произведение критического напряжения на площадь поперечного сечения стержня:

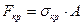(13.17)

На рис.13.2 приведена графическая зависимость критического напряжения от гибкости λ для стали марки Ст3. Для значений гибкости λ в пределах 0 – 40 критическое напряжение имеет постоянную величину. Для значений гибкости λ в пределах 40 – 100 критическое напряжение изменяется прямолинейно в соответствии с формулой Ясинского, а для значений гибкости λ от 100 до 200 критическое напряжение изменяется криволинейно и определяется по формуле Эйлера (кривая Эйлера).

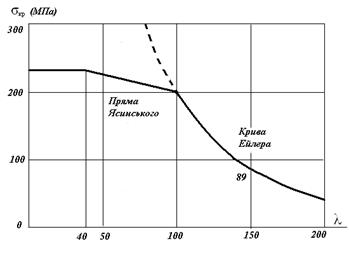
Рис.13.2