Определение критической силы сжатого стержня

Для упругого стержня, сжатого силой F (рис.13.1,а), составим уравнение изогнутой оси в безразличном состоянии, то есть при условии F = F_кр. При достижении силой F критического значения F_кр ось стержня искривляется и поперечные сечения стержня получают некоторые перемещения ν(x) в направлении осы y(рис.13.1,б), если изгибная жесткость сечения стержня относительно этой оси будет иметь большее значения от изгибной жесткости относительно перпендикулярной к ней оси zи наоборот, в направлении оси z (рис.13.1,в), если изгибная жесткость сечения стержня относительно этой оси будет иметь большее значения от изгибной жесткости относительно оси y,. Таким образом, искривление оси стержня всегда происходит в перпендикулярном направлении к оси поперечного сечения, относительно которой изгибная жесткость имеет минимальное значение EI_min.

Перемещение ν(x) рассматриваем как очень малое по сравнению с длиной стержня. При этом напряжения, которые возникают в поперечных сечениях стержня, не превосходят предела пропорциональности, то есть σ < σ_пц. В этих условиях мы имеем возможность использовать приближенное уравнение изогнутой оси деформированного стержня, то есть уравнение, полученное при рассмотрении поперечного изгиба балки:

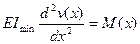(13.4)

где 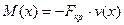, тогда:

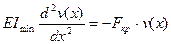, (13.5)

или 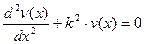, (13.6)

где 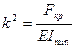(13.7)

Решением дифференциального уравнения (13.6) является известная гармоническая функция:

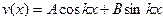(13.8)

Постоянные интегрирования А и B определяются из граничных условий закрепления стержня. При x = 0 имеем ν(0)= 0. Тогда из уравнения (13.8) находим А = 0. При этом уравнение прогибов упрощается и принимает вид:

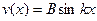(13.9)

При x = l, прогиб стержня также равняется нулю: ν(l) = 0, или

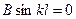
Последнее равенство возможно в двух случаях: 1) если В = 0 и 2) если .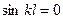

В первом случае отсутствуют прогибы стержня, то есть этот случай не отвечает условию поставленной задачи.

Во втором случае находим 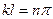. Возведем это равенство в квадрат 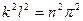и заменим 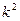его значением согласно зависимости (13.7). При этом, принимаем n = 1 (потому, что критическая сила имеет наименьшее значение из всех возможных), тогда получим формулу для определения критической силы стержня, который опирается на две шарнирные опоры:

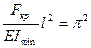, откуда 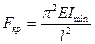(13.10)

Формула (13.10) впервые получена Эйлером и имеет название формулы Эйлера. Эта формула может быть обобщена и распространена на все случаи закрепления стержня путем замены действительной длины стержня l приведенной длиной μl. Где μ носит название коэффициента приведения длины стержня. Тогда обобщенная формула Эйлера будет иметь вид:

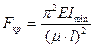(13.11)

Величина коэффициента приведения длины зависит от условий закрепления стержня. Возможные четыре случая закрепления стержня, для которых нужно знать (без доказательства) значения коэффициента μ:

1) Стержень закреплен по концам с помощью двух шарнирных опор (рис.13.1), тогда μ = 1.

2) Стержень закреплен на одном конце жесткой опорой (защемлением), тогда

μ = 2.

3) Стержень закреплен на одном конце жесткой опорой (защемлением), а на другом конце шарнирной опорой, тогда μ = 0,7.

4) Стержень закреплен на каждом конце жесткими опорами, тогда μ = 0,5.

Следует иметь в виду, что условия закрепления стержня в двух главных плоскостях инерции поперечного сечения стержня могут быть одинаковыми, а могут быть разными. В первом случае расчет на устойчивость осуществляется в плоскости минимальной изгибной жесткости, а во втором случае расчет выполняется в каждой из главных плоскостей.