Примеры расчета на кручение
Пример 12.1 На стальний вал, который вращается в подшипниковых опорах А и Д со скоростью 180 оборотов за минуту, насажено в точках Б, В, Г три шкива 1,2 и 3 (рис.12.7,а). Шкив 2 получает от двигателя мощность 75 кВт и передает ее на шкивы 1 и 3 в пропорции 1:2. Требуется: 1) построить епюру крутящих моментов;
2) определить необходимый диаметр сплошного поперечного сечения вала из условий прочности и жесткости, приняв 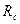 =40 МПа,
=40 МПа, 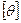 =0,0053 рад/п.м, G=0,8·105 МПа;
=0,0053 рад/п.м, G=0,8·105 МПа;
3) определить внутренний и внешний диаметры пустотелого сечения вала при отношении этих диаметров 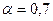 из тех же условий, что и сплошного;
из тех же условий, что и сплошного;
4) построить епюру углов закручивания вала сплошного поперечного сечения.
Решение задачи. 1) Определяем внешние моменты, которые действуют на шкивы 1,2 и 3 соответственно. Учитывая, что m1 + m3 = m2= 75 кВт, а m3= 2 m2, получим: 3m1 = 75 кВт, откуда m1= 25 кВт, а m3 = 50 кВт.
Используя формулу (12.4) определяем внешние моменты в кНм: m1= 9,551·25/180= 1,33 кНм; m2= 9,551·75/180 = 3,99 кНм;
m3= 9,551·50/180 = 2,66 кНм.
Делим вал на четыре участка АБ, БВ, ВГ и ГД и определяем крутящие моменты на каждом из них, рассматривая равновесие левых частей вала относительно произвольных сечений каждого участка. На рис.12.7,б приведенная схема нагрузки вала внешними моментами и показаны произвольные сечения 1-1, 2-2, 3-3 и 4-4 на каждом участке.
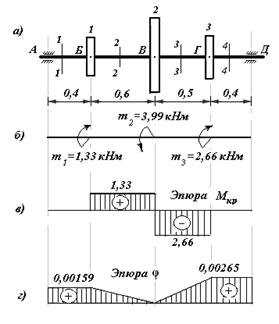
Рис.12.7
Слева от сечения 1-1 отсутствует внешняя нагрузка, поэтому крутящий момент на участке АБ равняется нулю ( 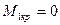 ).
).
Слева от сечения 2-2 действует внешний момент m1 равный 1,33 кНм инаправленный по часовой стрелке. Крутящий момент на участке БВ равняется этому моменту m1 с положительным знаком ( 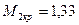 кНм).
кНм).
Слева от сечения 3-3 действует внешний момент m3 равный 2,66 кНм и направленный против часовой стрелки, поэтому крутящий момент на участке ВГ равняется этому моменту с отрицательным знаком ( 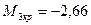 кНм).
кНм).
Наконец, справа от сечения 4-4 отсутствует внешняя нагрузка, поэтому крутящий момент на участке ГД равняется нулю ( 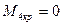 ). На рис.12.7,в построенная эпюра крутящих моментов.
). На рис.12.7,в построенная эпюра крутящих моментов.
2) Определяем необходимый диаметр сплошного поперечного сечения вала из условия прочности. Для этого используем формулу (12.18):
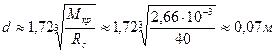 , принимаем
, принимаем 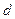 =70 мм
=70 мм
Определяем необходимые внешний и внутренний диаметры полого сечения вала из условия прочности. Используя формулу (12.19), находим:
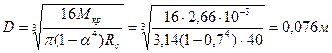 , или
, или 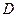 =7,6 см, тогда
=7,6 см, тогда  =0,7·7,6=5,3 см
=0,7·7,6=5,3 см
Площадь сплошного поперечного сечения равняется:
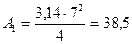 см2
см2
Площадь полого сечения вала равняется:
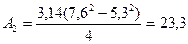 см2
см2
Таким образом, площадь сплошного сечения больше площади полого сечения вала в 1,65 раза.
3) Определяем диаметр сплошного сечения вала из условия жесткости (12.21).
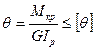 , откуда
, откуда
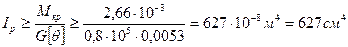 ,
,
учитывая, что 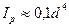 , найдем
, найдем 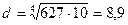 см. Аналогично определяем внешний и внутренний диаметры полого сечения:
см. Аналогично определяем внешний и внутренний диаметры полого сечения: 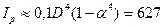 , откуда
, откуда
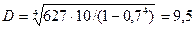 см и
см и 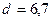 см.
см.
Из двух значений диаметров поперечного сечения вала, как сплошного, так и полого, нужно принять большие значения, то есть значения, которые определены из условия жесткости.
4) Определяем углы закручивания на каждом участке вала. Примем условно неподвижным сечение вала, в котором насажен шкив 2, тогда, шкив 1 повернется относительно шкива 2 на угол:
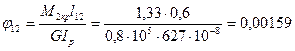 радиан.
радиан.
Углы закручивания сечений вала на первом участке АБ имеют постоянную величину, которая равняется углу закручивания шкива 1 относительно шкива 2.
Аналогично шкив 3 повернется относительно шкива 2 в том же направлении на угол:
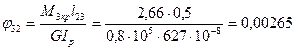 радиан.
радиан.
При этом углы закручивания сечений вала на участке ГД будут равняться углу закручивания шкива 3 относительно шкива 2.
Эпюра углов закручивания построенная на рис.12.7,г.
Пример 6.2 Цилиндрическая стальна пружина диаметром 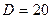 см закреплена вверху и нагруженная внизу силой растяжения F=40 кН. Определить диаметр провода пружины, если допустимое напряжение равняется
см закреплена вверху и нагруженная внизу силой растяжения F=40 кН. Определить диаметр провода пружины, если допустимое напряжение равняется 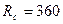 МПа, а также удлинения пружины при количестве витков n=8.
МПа, а также удлинения пружины при количестве витков n=8.
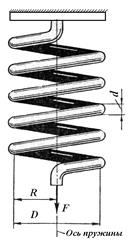
Рис.12.8
Решение задачи. 1) Определяем диаметр проволоки пружины из условия прочности (12.26), без учета отношения диаметра проволоки к удвоенному диаметру пружины, т.е используем условие прочности:
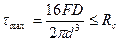
подставим исходные данные задачи
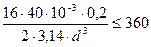 , откуда
, откуда
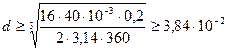 м, или
м, или 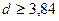 см. Принимаем
см. Принимаем 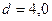 см. (Делаем округление к величине стандартного диаметра проволоки).
см. (Делаем округление к величине стандартного диаметра проволоки).
Проверим выполнение условия прочности (12.26):
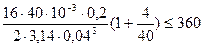 , откуда получаем
, откуда получаем 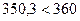 , то есть условие прочности выполняется.
, то есть условие прочности выполняется.
2) Определяем удлинение пружины, используя формулу (12.27):
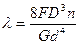 ,тогда
,тогда 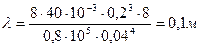 , или
, или 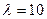 см.
см.
Дата добавления: 2018-11-26; просмотров: 1230;











