Дискретизация непрерывных сигналов по времени

При использовании цифровой обработки сигнала (ЦОС) вместо непрерывной величины обрабатывается дискретная цифровая последовательность. При переходе от аналоговой формы представления информации к цифровой необходимо в первую очередь решить вопрос:

Как без потери информации представить непрерывное входное напряжение числовой последовательностью в виде отдельных отсчетов (дискрет)?

В основе дискретизации непрерывных сигналов лежит принципиальная возможность представления их в виде взвешенных сумм

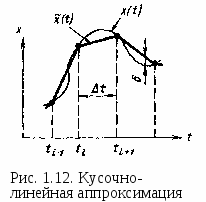
где а_п — некоторые коэффициенты или отсчеты, характеризующие исходный сигнал в дискретные моменты времени; f_n(t) — набор элементарных функций, используемых для восстановлении сигнала по его отсчетам (рис. 1.12).

Многочисленные системы дискретного представления непрерывных сигналов можно разделить на системы, использующие постоянный период дискретизации (равномерная дискретизация) и переменный (адаптивная дискретизация).

Наиболее распространенной формой дискретизации является равномерная, в основе которой лежит теорема отсчетов (или теорема Котельникова–Найквиста):

Всякий непрерывный сигнал, имеющий ограниченный частотный спектр, полностью определяется своими дискретными значениями в моменты отсчета, отстоящими друг от друга на интервалы времени не более Dt=1/2F_max, где F_max– максимальная частота в спектре сигнала.

Согласно этой теореме, в качестве коэффициентов а_n необходимо использовать мгновенные значения сигнала x(t_n) в дискретные моменты времени t_n=nDt, а период дискретизации выбирать из условия

Dt£ 1/2F_max (1.15)

где F_m — максимальная частота спектра исходного сигнала.