ГЛАВА 2. ПРЕОБРАЗОВАНИЕ НЕПРЕРЫВНЫХ СИГНАЛОВ В ДИСКРЕТНЫЕ

§ 2.1. ПРЕИМУЩЕСТВА ЦИФРОВОЙ ФОРМЫ ПРЕДСТАВЛЕНИЯ СИГНАЛОВ

В любую систему информация поступает в виде сигналов. Различные параметры физических процессов с помощью датчиков обычно преобразуются в электрические сигналы. Как правило, ими являются непрерывно изменяющиеся ток или напряжение, но возможно поступление и импульсных сигналов, как, например. в радиолокации. Печатный текст отображается буквами, цифрами и другими знаками.

Хотя поступающую информацию можно хранить, передавать и обрабатывать как в виде непрерывных, так и в виде дискретных сигналов, на современном этапе развития информационной техники предпочтение отдается дискретным сигналам, поэтому сигналы, как правило, преобразуются в дискретные. С этой целью каждый непрерывный сигнал подвергается операциям квантования по времени (дискретизации) и по уровню.

Под дискретизацией подразумевают, преобразование функции непрерывного времени в функцию дискретного времени, представляемую совокупностью величин, называемых координатами, по значениям которых исходная непрерывная функция может быть восстановлена с заданной точностью. Роль координат часто выполняют мгновенные значения функции, отсчитанные в определенные моменты времени.

Под квантованием подразумевают преобразование некоторой величины с непрерывной шкалой значений в величину, имеющую дискретную шкалу значений. Оно сводится к замене любого мгновенного значения одним из конечного множества разрешенных значений, называемых уровнями квантования.

Изменение вида сигнала u(t) (рис. 2.1, а) в результате проведения операции дискретизации показано на рис. 2.1,6, а в результате совместного проведения операций дискретизации и квантования — на рис. 2.1, в.

Число уровней квантования на рис. 2.1,в равно 8. Обычно их значительно больше. Передача такого множества различных по уровню импульсов даже на небольшие расстояния применяется крайне редко. Если провести нумерацию уровней, то их передача сведется к передаче чисел. Тогда, выразив эти числа в какой-либо системе счисления, можно обойтись меньшим множеством передаваемых сигналов. Как правило, дискретный сигнал преобразуется в последовательность чисел, выраженных в двоичном коде. Каждое дискретное значение сигнала представляется в этом случае последовательностью сигналов двух уровней. Наличие или отсутствие импульса на определенном месте интерпретируется единицей или нулем в соответствующем разряде двоичного числа.

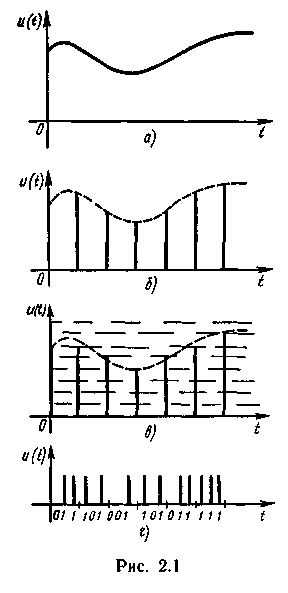Цифровая форма представления сигнала u(t) (рис. 2.1, а) показана на рис. 2.1, г. Для восьми уровней достаточно трех двоичных разрядов. Импульсы старших разрядов расположены крайними справа.

Причины перехода к дискретному и цифровому выражению информации заключаются в следующем.

Для конкретных задач управления или исследования интересующего нас объекта обычно требуется значительно меньше информации, чем ее поступает с датчиков в виде сигналов, изменяющихся во времени непрерывно. Учет априорных сведений об этих сигналах и целях их получения позволяет ограничиться отсчетами, взятыми через определенные моменты времени.

При неизбежных флуктуациях во времени интересующих нас параметров и конечной погрешности средств измерения информация о величине сигнала в каждый момент отсчета всегда ограничена, что и выражается в конечном числе уровней квантования. Кроме того, специфика решаемых в системе задач часто такова, что целесообразно ограничиться значительно меньшим числом уровней, чем следует из указанных выше ограничений.

Во многих случаях информация извлекается и передается с целью дальнейшей обработки средствами цифровой техники, в первую очередь ЭВМ и микропроцессорами. Рациональное выполнение операций дискретизации и квантования при этом приводит к значительному экономическому эффекту как за счет снижения затрат на хранение и обработку получаемой информации, так и вследствие сокращения времени обработки информации, что ведет к улучшению качества управления.

При передаче и обработке информации в цифровой технике существует принципиальная возможность снижения вероятности получения ошибочного результата до весьма малых значений. Она возникает потому, что при использовании дискретных сигналов, во-первых, применимы такие методы кодирования, которые обеспечивают обнаружение и исправление ошибок (они изложены в гл. 6), а во-вторых, можно избежать свойственного аналоговым сигналам эффекта накопления искажений в процессе их передачи и обработки, поскольку квантованный сигнал легко восстановить до первоначального уровня всякий раз, когда величина накопленных искажений приблизится к половине кванта. Практическая реализация указанных методов наиболее эффективна при минимальном числе уровней, равном двум.

Выражение информации в цифровой форме облегчает унификацию операций ее преобразования на всех этапах обращения. Массовость изготовления типовых узлов и блоков, простота их настройки, отсутствие необходимости регулировки в процессе эксплуатации позволяют, в свою очередь, улучшить такие важнейшие технико-экономические показатели средств цифровой техники, как стоимость изготовления и эксплуатации, а также надежность.

Низкая стоимость и высокая надежность больших интегральных схем, естественно, являются мощными стимулами дальнейшего расширения областей использования цифровых сигналов.

В данной главе мы ограничимся рассмотрением методов преобразования непрерывных сигналов в дискретные. Вопросы выражения дискретных сигналов в цифровой форме изложены в гл. 5.

§ 2.2. ОБЩАЯ ПОСТАНОВКА ЗАДАЧИ ДИСКРЕТИЗАЦИИ

В самом общем случае представление непрерывного сигнала u(t) на интервале Т совокупностью координат (с₁, с₂, ..., c_N) может быть записано в виде

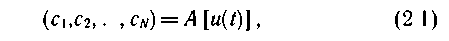
где А — оператор дискретного представления сигнала, реализуемый устройством, называемым дискретизатором.

Аналогично можно записать и операцию восстановления по совокупности координат (с₁, c_2, ..., c_N) непрерывной функции u*(t) (воспроизводящей функции), отображающей исходный сигнал с некоторой текущей погрешностью приближения d(t) = u(t) — u*(t):

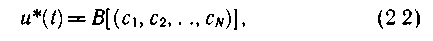
где В — оператор восстановления, реализуемый устройством восстановления сигнала.

Задача дискретизации в математическом плане сводится к совместному выбору пары операторов A и B, обеспечивающих заданную точность восстановления сигнала.

Рассмотрим разновидности используемых операторов A и B и критериев оценки точности восстановления сигнала.

Широкое практическое применение нашли линейные операторы, поскольку их техническая реализация проще. Для определения координат сигнала используется соотношение

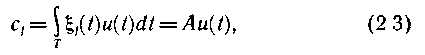
где {ξ_j(t)} 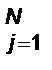- система функций, которые для определенности назовем весовыми.