ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ

6.1. Равнодействующая системы сходящихся сил в прост­ранстве. Условия и уравнения равновесия

Силы, не лежащие в одной плоскости, составляют пространствен­ную систему. Если линии действия все сил пересекаются в одной точ­ке, то пространственную систему называют системой сходящихся сил.

Пусть в точке А твердого тела приложены силы 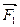, , 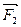,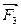…, 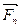(рис.6.1) и требуется найти величину и направление их равнодейст­вующей .

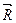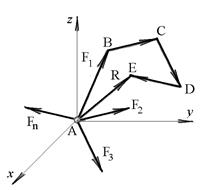
Рис.6.1

Любые две силы заданной системы располагаются в одной плос­кости, поэтому их равнодействующая определяется по правилу параллелограмма или треугольника сил

(см. § 5). Осуществляя пос­ледовательное сложение заданных сил по правилу силового треуголь­ника, получим многоугольник ABCDE, стороны которого геометри­чески равны заданным силам и не лежат в одной плоскости. Замыкаю­щая сторона АE этого многоугольника является равнодействующей всех сил рассматриваемой системы. Следовательно, равнодействующая системы сходящихся сил расположенных в пространстве, равна их геомет­рической сумме:

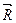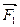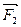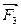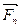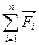= + + +…+ = (6.1)

Если при построении силового многоугольника соблюдается масш­таб сил μ_с, параллельность его сторон линиям действия заданных сил, то модуль равнодействующей можно определить измерением замы­кающей стороны АЕ многоугольника сил в принятом масштабе, т.е.

R = μ_с,∙АЕ (6.2)

При построении многоугольника сил может оказаться, что конец вектора, геометрически равного последней силе 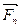_, совпадает с на­чалом первой силы, т.е. с точкой А. В этом случае, замыкающая сто­рона многоугольника отсутствует, а сам многоугольник является зам­кнутым. Все стороны этого многоугольника имеют одинаковые направления при обходе его контура по ходу часовой стрелки или против. Условие, при котором многоугольник сил замкнут, является геометрическим условием равновесия пространственной системы сил.

В частном случае равнодействующая трех сил, не лежащих в одной плоскости (рис.59), определяется диагональю параллелепипеда, пос­троенного на этих силах. В самом деле, при сложении сил 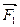и 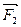получаем их равнодействующую 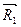, которая выражается диагональю 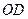параллелограмма .

= +

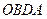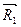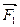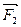
Полученная сила 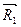лежит в одной плоскости с силой 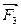. Поэтому их равнодействующая 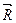определится диагональю 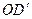параллелограмма 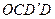, т.е.

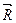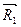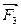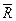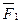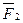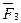= + , или = + + (6.3)

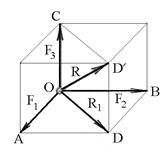
Рис.6.2

Из рисунка 6.2 видно, что диагональ 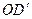параллелограмма 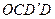совпадает с диагональю параллелепипеда, построенного на трех заданных силах.

Правило сложения трех сил, расположенных в разных плоскостях называется правилом параллелепипеда сил. Используя это правило мож­но разложить любую силу на три взаимно перпендикулярные составляю­щие. Для этого удобно совместить начало прямоугольной системы коор­динат с началом вектора силы, а из его конца опустить перпендику­ляры к координатным плоскостям и осям.

Вернемся теперь к равнодействующей 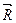системы сходящихся сил, найденной геометрическим путем на рис.6.1 и разложим её три взаим­но перпендикулярные составляющие, направленные вдоль координатных осей х , у , z (рис.6.3). Легко заметить, что найденные составля­ющие равны проекциям равнодействующей 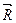на координатные оси.

Обо­значим углы между равнодействующей 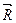и осями х , у , z соответственно через α , β , γ. Тогда проекции равнодействующей на ука­занные оси будут определяться выражениями:

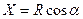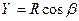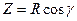, , (6.4)

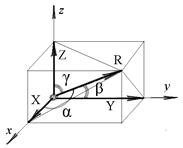
Рис.6.3

Выражения (6.4) позволяют также определить направление равнодейст­вующей в пространстве, т.е. углы α , β , γ , если известны её модуль R, и её проекции X , Y , Z на координатные оси.

Поскольку проекции равнодействующей являются ребрами прямо­угольного параллелепипеда, а сама равнодействующая - его диаго­налью, то модуль R определится известным выражением:

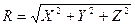(6.5)

В § 9 было установлено, что проекция равнодействующей на любую ось равна алгебраической сумме проекций всех сил на ту же ось, т.е.

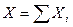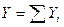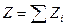, , (6.6)

Докажем условия, при которых пространственная система сходя­щихся сил будет находиться в равновесии. Как установлено ранее, пространственная система сходящихся сил приводится к одной рав­нодействующей 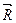. Если равнодействующая заданных сил равна нулю, то под действием таких сил твердое тело находится в равновесии. Из выражения (6.4) следует, что равнодействующая 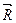может быть равной нулю только в том случае, когда её проекции на каждую из трех взаимно перпендикулярных осей одновременно равны нулю, т.е. Х= 0, Y=0 и Z=0. Учитывая равенства (6.6), получаем следую­щие условия равновесия пространственной системы сходящихся сил:

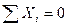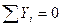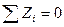, , (6.7)

Итак, для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы одновременно были равными нулю алгебраические суммы проекций всех сил на три взаимно перпендику­лярные оси x, у и z .

Уравнения равновесия вытекают из условий (6.7) при подробном вычислении их левых частей путем суммирования проекций всех задан­ных сил и неизвестных реакций связей рассматриваемого тела на со­ответствующие координатные оси. В случае, когда все силы равновес­ной системы известны, уравнения равновесия обращаются в тождест­ва

0 = 0.