Главный вектор и главный момент

Рассмотрим задачу приведения системы сил, произвольно располо­женных в одной плоскости к произвольному центру.

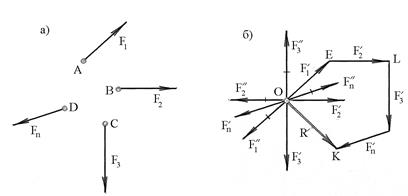
Рис.4.3

Пусть заданы силы 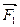, , 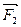,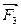…, , 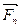(рис.4.3,а) и точка О в плос­кости, в которой действуют заданные силы. Воспользуемся правилом приведения силы к задан­ному центру, рассмотренным в § 4.2.

Приложим в центре приведения О по две противоположно направленные силы, которые соответственно равны и параллельны каждой из заданных сил. В результате получим:

а) систему сил 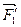, , 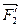,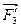… , 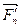приложенных в точке О. Поль­зуясь правилом сложения системы сходящихся сил, найдем замыкающий вектор ОК = 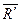силового многоугольника ОEL..K (рис.4.3,б), кото­рый называется главным вектором системы заданных сил и равен их геометрической сумме:

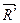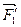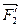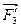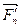= + + +…+ (4.3)

Следует иметь в виду, что главный вектор не эквивалентен равно­действующей заданных сил, так как линии их действия не совпадают.

Используя метод проекций и формулы, полученные в § 2.6., легко вычислить модуль и определить направление главного вектора по отношению к выбранной системе координатных осей.

б) Систему присоединенных пар: ( , ); ( , ); ( , );…( , ).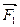

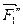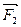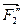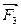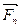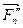Согласно приведенному в § 4.2. определению, моменты присоединенных пар равны моментам заданных сил относительно точки О, т.е.

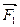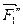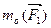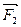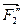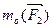m( , )= , m( 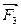, )= 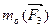, m( , )= … m( 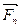, 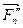)= 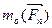Известно, что система пар, расположенных в одной плос­кости, приводится к результирующей паре, момент которой равен сумме моментов составляющих пар. Этот момент носит название главного мо­мента системы заданных сил относительно центра приведения и опреде­ляется выражением:

m_o= + + +…+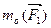

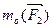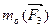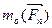
(4.4)

Итак, система как угодно расположенных на плоскости сил приво­дится к одной силе, приложенной в центре приведения О и равной глав­ному вектору 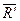и к одной паре, момент которой равен главному момен­ту заданных сил относительно центра О.

Для определения модуля и направления главного вектора 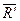целе­сообразно воспользоваться методом проекций, подробно изложенным в § 2.6., а для вычисления главного момента необходимо установить рас­стояния от центра приведения О до линий действия заданных сил и най­ти алгебраическую сумму моментов этих сил относительно центра приве­дения (формула 4.4).