Приведение силы к заданному центру.

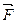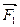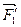Пусть к твердому телу в его точке А приложена сила (рис.4.2). Возьмем произвольную точку О, расположенную в той же плоскости что и заданная сила и приложим к ней две противоположно направленные силы и, , модули которых равны модулю заданной силы, а их ли­ния действия параллельна линии действия силы .

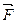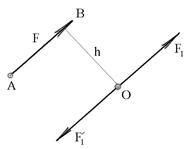
Рис.4.2

Система трех сил 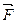, , 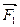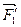эквивалентна заданной силе 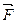, согласно второй аксиоме статики. Силу 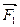называют статически равной силе 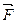, так как модули и направления этих сил совпадают, а линии их действия параллельны. Можно говорить также, что сила 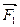является заданной силой 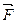, перенесенной параллельно её линии действия (самой себе) в точку О.

Силы 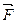и 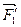образуют пару, которая называется присоединенной парой. Момент присоединенной пары определяется выражением (4.1).

Таким образом, любая сила может быть приведена к произвольной точке О плоскости путем замены её действия такой же силой, приложенной в точ­ке О и присоединенной парой, момент которой равен моменту заданной силы относительно точки О.

Приведение плоской системы сил к заданному центру.