Приложение теории пар к решению задач строительной практики.
Пример 3.1. Недеформируемый стержень (вал) загружен тремя парами сил, расположенными в плоскостях, перпендикулярных к оси стержня (рис.3.9). Моменты пар соответственно равны: m1 = 12 кНмm2 = 8 кНм, m3 = 14 кНм.
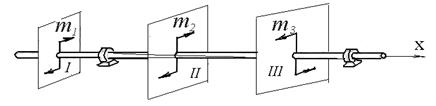
Рис.3.9
Требуется определить момент равнодействующей пары и установить направление вращения вала.
Решение. На основании второго свойства пар, две из заданных пар могут быть перенесены в плоскость действия третьей, например, в плоскость I. В результате получаем возможность для сложения пар по формуле (3.13):
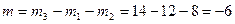 кНм.
кНм.
Так как момент результирующей пары имеет знак минус, то вращение стержня будет происходить в направлении действия пар, расположенных в плоскостях I и II т.е. по ходу часовой стрелки, если смотреть с конца оси x..
Пример 3.2. Балка АВ длиной 5 м заложена в стену толщиной 1 м (рис.3.10,а) и опирается на неё в точках В и С. Балка нагружена в точке А вертикальной силой
F = 10 кН.. Определить силы давления балки в точках В и С.
Решение. Учитывая характер связей балки в точках В и С, устанавливаем направления реакций, нормальные к оси балки. Реакцию  в точке В направим вниз, а реакцию
в точке В направим вниз, а реакцию  в точке С направим вверх и разложим её на две составляющие
в точке С направим вверх и разложим её на две составляющие 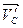 и
и 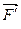 . Четыре силы, представленные на рис.3.10,б образуют две пары, под действием которых балка находится в равновесии.
. Четыре силы, представленные на рис.3.10,б образуют две пары, под действием которых балка находится в равновесии.
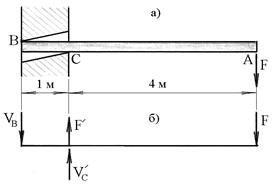
Рис.3.10
Используя условие равновесия пар, составим уравнение равновесия:
т( 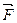 ,
, 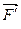 )+ т(
)+ т( 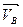 ,
, 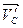 ) = 0, где: т(
) = 0, где: т( 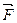 ,
, 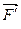 )=-F∙4=-10∙4=-40 кНм и
)=-F∙4=-10∙4=-40 кНм и
т( 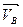 ,
, 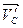 ) =
) = 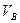 ∙1=
∙1= 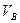
Следовательно, -40+ 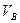 =0,
=0, 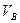 =
= 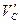 =40 кН
=40 кН
Учитывая, что реакция в точке С равна сумме двух сил 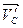 и
и 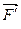 ходим:
ходим:
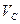 =
= 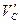 +
+ 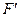 = 40+10 = 50 кн.
= 40+10 = 50 кн.
Пример 3.3. Поворотный кран, схема которого представлена на рис.3.11,а поднимает груз 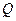 = 150 кН. Определить реакции подшипника А и подпятника В этого крана.
= 150 кН. Определить реакции подшипника А и подпятника В этого крана.
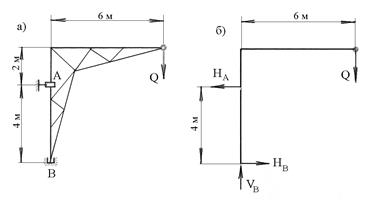
Рис.3.11
Решение. В подшипнике А возникает горизонтальная реакция 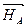 , а реакция подпятника В может быть разложена на две составляющие: горизонтальную
, а реакция подпятника В может быть разложена на две составляющие: горизонтальную 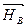 и вертикальную
и вертикальную 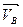 (рис.3.11,б).
(рис.3.11,б).
Действующие на кран силы образуют две пары, которые находятся в равновесии. Следовательно, алгебраическая сумма моментов этих пар равна нулю, т.е.
т( 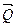 ,
, 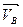 ) + т(
) + т( 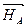 ,
, 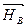 ) = 0, или
) = 0, или
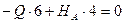 , откуда
, откуда 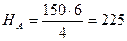 кН.
кН.
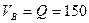 кН.
кН.
Вопросы для самоконтроля полученных знаний.
1) Какие силы называются парой сил?
2) Чем характеризуется механический эффект действия пары сил на тело?
3) Как определяется момент пары сил?
4) В каком случае момент пары сил имеет знак +(плюс) и в каком случае – знак – (минус)?
5) Может ли пара сил быть перенесенной в другое место в плоскости её действия?
6) Может ли пара сил быть перенесенной в другую плоскость? При каком условии это возможно?
7) Что такое система пар сил? Что такое равнодействующая пара? Как определяется момент равнодействующей пары?
8) При каком условии система пар на плоскости будет находиться в равновесии?
Дата добавления: 2018-11-26; просмотров: 1111;











