Момент силы относительно точки.

Если линии действия сил не параллельны и не пересекаются в одной точке, то имеет место общий случай расположения сил на плос­кости или в пространстве. В настоящей главе рассматриваются силы, действующие в одной плоскости. Для получения метода их сложения вводится понятие момента силы относительно произвольной точки.

Рассмотрим некоторую силу 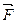(рис.4.1), представленную направ­ленным отрезком 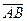. Возьмем произвольную точку O в стороне от силы 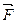и опустим из неё перпендикуляр на линию действия заданной силы. Длина h проведенного перпендикуляра между точкой и силой называется плечом силы 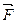относительно точки O.

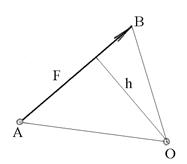
Рис.4.1

Произведение модуля силы на плечо h, взятое со знаком +(плюс) или –(минус), называется моментом этой силы 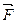относи­тельно точки О и обозначается символом 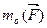. Следовательно:

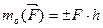(4.1)

В правой части выражения (4.1) сохраняют положительный знак, если сила 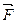относительно точки О стремится повернуть плоскость, в которой она действует, против часовой стрелки. Момент силы при­нимается отрицательным, если сила относительно точки О стремится повернуть плоскость в направлении часовой стрелки.

Указанное выше правило знаков является чисто условным. Строго­сть и точность выкладок и практических решений не нарушится, если изменить правило знаков момента.

Соединим, далее, точку О с точками А и В, т.е. с началом и кон­цом рассматриваемой силы 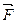. В результате получим треугольник АОВ, площадь которого равна:

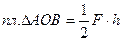
но 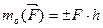, следовательно:

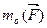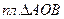= ± 2 (4.2)

Итак, момент силы относительно точки численно равен удвоенной площади треугольника, основанием которого является сила 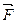, а вер­шиной точка О.

С приближением точки О к линии действия силы 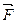, момент силы относительно этой точки уменьшается и становится равным нулю, если линия действия силы проходит через точку О.

Размерность момента силы относительно точки та же, что и размерность момента пары сил.