Сил. Три вида условий равновесия

Необходимыми и достаточными условиями равновесия плоской сис­темы сил являются условия равенства нулю главного вектора и глав­ного момента этих сил, т.е.

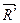= 0 и m₀ = 0.

Модуль главного вектора определяется по известной формуле:

,

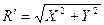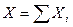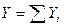где и - проекции главного вектора на координатные оси x и y соответственно. Из приведенной формулы следует, что главный вектор может быть равным нулю, если равны нулю одновремен­но его проекции на две взаимно перпендикулярные оси, т.е. есл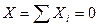и

и ,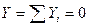

Главный момент системы сил, произвольно расположенных в плоскости также должен равняться нулю, т.е. .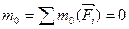

В результате получаем три следующих условия равновесия плоской системы сил:

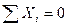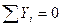, и 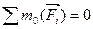, (4.10)

Итак, система сил, произвольно расположенных в одной плоскос­ти находится в равновесии, если:

а алгебраическая сумма проекций всех сил на координатную ось x равна нулю;

б) алгебраическая сумма проекций всех сил на координатную ось y равна нулю;

в) алгебраическая сумма моментов всех сил относительно произвольной точки О плоскости равна нулю.

Выражения (4.10) представляют первый или основной вид условий равновесия. При составлении уравнений равновесия с использованием условий (4.10) необходимо рационально выбирать направления осей проекций и положение моментной точки О, чтобы полученные уравнения были наиболее простыми.

Второй вид условий равновесия состоит в том, что вместо условия равенства нулю суммы проекций на одну из осей, обычно на ось y, принимается условие равенства нулю суммы моментов всех сил относительно другой произвольной точки А, т.е

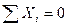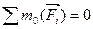, и 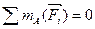(4.11)

Таким образом, для равновесия плоской системы сил необходимо и достаточно чтобы были равными нулю:

а) сумма проекций всех сил на произвольную ось x;

б) суммы моментов всех сил относительно двух произвольно выбранных

точек О и А.

Система сил, произвольно расположенных в плоскости, будет на­ходиться в равновесии и в том случае, когда равны нулю суммы мо­ментов всех сил относительно трех любых точек О, А, В, не лежащих на одной прямой, т.е:

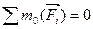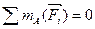, и 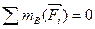(4.12)

Выражения (4.12) являются условиями равновесия третьего вида.

Система параллельных сил на плоскости (рис.4.6) является част­ным случаем системы произвольно расположенных сил, поэтому усло­вия её равновесия могут быть получены из общих условий равновесия (4.10).

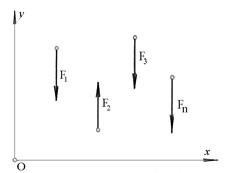
Рис.4.6

Выберем систему координат xOy так, чтобы ось y была параллельной заданным силам. Тогда сумма проекций всех сил на ось х. будет тож­дественно равна нулю, и для равновесия системы параллель­ных сил необходимо и достаточно выполнить два следующие условия:

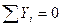и 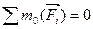(4.13)

Первое из условий (4.13) можно заменить условием равенства нулю суммы моментов всех параллельных сил относительно другой точки плоскости, не совпадающей с точкой О и не лежащей с ней на одной прямой, параллельной заданным силам. В результате приходим ко второму виду условий равновесия:

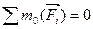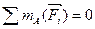, (4.14)

В этом случае условие 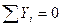используется для контроля пра­вильности решения задач.

Рассмотрим несколько примеров на равновесие тел под действием системы сил, как угодно расположенных в плоскости и системы параллельных сил.

Пример 4.1. Твердое тело АВ весом Q = 80 кН закреплено в точ­ках А и В при помощи трех стержней (рис.4.6). Определить усилия в стержнях, возникающие от действия активной силы .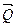

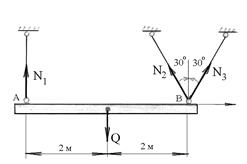
Рис.4.6

Решение. Освобождаем мысленно закрепленное тело от стержневых связей и их действие компенсируем приложением неизвестных по величине реакций 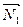, , 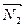, 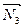численно равных искомым усилиям в стержнях. В результате тело АВ будет находиться в равновесии под действием четырех сил, произвольно расположенных в плоскости чертежа (рис.4.6).

Воспользуемся условиями равновесия второго вида, приняв нап­равление оси x перпендикулярным силам 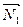и 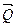, а также приняв точки А и В в качестве моментных точек. Запишем эти условия:

, ,

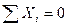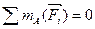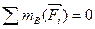
Составляем уравнения равновесия, используя эти условия:

1) 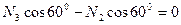, откуда находим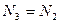

2) 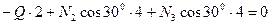, учитывая, что

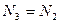, находим из этого уравнения 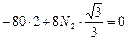, откуда получаем

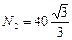кН.

3) 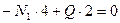, откуда определяем 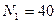кН

Для проверки найденных значений используем условие равновесия в форме проекции всех сил на вертикальную ось y.

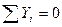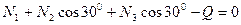- . После подстановки найденных значений усилий в стержнях, получим:

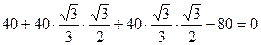или 80-80=0.

Таким образом, усилия в стержнях определены верно.

Пример 4.2. Тело весом Q = 12 кН подвешено в точке В при по­мощи троса (гибкой нити), опирается в точке А на шарнирно неподвиж­ную опору и загружено в точке С вертикальной силой F = 3 кН. (рис.4.7). Тре­буется определить силу натяжения троса N и реакцию шарнирной опоры.

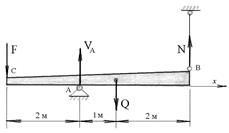
Рис.4.7

Решение. Известно, что реакция троса всегда направлена вдоль его геометрической оси, а реакция шарнирной опоры может иметь лю­бое направление на плоскости. Однако в рассматриваемом случае все заданные силы и усилие в тросе параллельны между собой, следова­тельно, реакция шарнирной опоры должна быть им параллельна. На рис.4.7 показаны четыре силы, под действием которых рассматриваемое тело находится в равновесии.

В качестве условий равновесия принимаем:

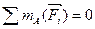и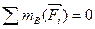

Эти условия приводят к уравнениям с разделенными неизвестными, так как линия действия одной из неизвестных проходит через моментную точку. Составим уравнения равновесия:

1) 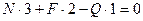, откуда 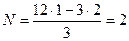кН.

2) 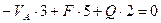, откуда 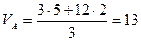кН.

Для проверки правильности решения примера используем условие равенства нулю суммы проекций всех сил на вертикальную им ось y.

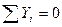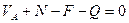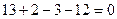- или , 0=0

Вопросы для самоконтроля полученных знаний

1) Что такое момент силы относительно точки? Как он определяется?

2) Может ли момент силы относительно точки иметь знак – (минус)?

3) Как осуществляется приведение силы к точке плоскости?

4) Чем заменяется действие силы при приведении её к точке (центру)?

5) Как осуществляется приведение плоской системы сил к выбранному центру?

6) Что такое главный вектор плоской системы сил? Чему он равен и зависит ли он от выбора центра приведения?

7) Что такое главный момент плоской системы сил? Чему он равен и зависит ли он от выбора центра приведения?

8) В каком случае плоская система произвольно расположенных сил находится в равновесии?

9) Сформулируйте и докажите теорему Вариньона для плоской системы сил.

10) Как находится равнодействующая плоской системы сил графическим способом?

11) Что такое силовой многоугольник (план сил)?

12) Что такое веревочный многоугольник? Как определяется точка плоскости, через которую проходит линия действия равнодействующей плоской системы сил?

13) Какие виды условий равновесия плоской системы сил можно использовать при решении задач?