Влияние температуры на скорость реакции. Энергия активации
В общем случае скорость химической реакции с повышением температуры увеличивается. Поскольку  , то влияние температуры на скорость выражается через влияние температуры на «К», поскольку концентрация от температуры практически не меняется. Опыт показывает, что при повышении температуры на 10 0С скорость реакции возрастает в 2 – 4 раза (правило Вант-Гоффа). Для характеристики зависимости скорости химической реакции от температуры был выведен температурный коэффициент скорости реакции:
, то влияние температуры на скорость выражается через влияние температуры на «К», поскольку концентрация от температуры практически не меняется. Опыт показывает, что при повышении температуры на 10 0С скорость реакции возрастает в 2 – 4 раза (правило Вант-Гоффа). Для характеристики зависимости скорости химической реакции от температуры был выведен температурный коэффициент скорости реакции:
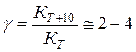
Если известны константы скорости при температурах, отличающихся не на 10 0С, то коэффициент Вант-Гоффа может быть определен из уравнения:
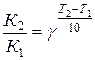
где К2 и К1 – константы скорости при температурах Т2 и Т1.
Более строгую зависимость от температуры константы скорости дает уравнение:
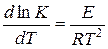
которое получило название уравнения Аррениуса. Величина «Е» имеет размерность энергии и носит название энергии активации.
Энергию активации можно определить как тот избыток энергии по сравнению со средней энергией молекул при данной температуре, которым должны обладать молекулы, чтобы они могли легко вступить в химическую реакцию. Поскольку Е > 0, то производная 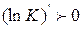 следовательно, lnK и К будут всегда возрастать с ростом Т.
следовательно, lnK и К будут всегда возрастать с ростом Т.
Связь энергии активации с тепловым эффектом можно проиллюстрировать с помощью представления об энергетическом барьере. Химическую реакцию можно представить как переход системы из энергетического состояния 1 в состояние 2, сопровождающееся тепловым эффектом 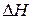 (при р = const). Из рисунка 3 видно, что переход из состояния 1 в состояние 2 возможен при затрате энергии Е, а обратный переход возможен при затрате энергии Е’. Поскольку Е’ > Е, то есть энергетический барьер обратной реакции будет больше, чем прямой, следовательно скорость обратной реакции будет меньше скорости прямой.
(при р = const). Из рисунка 3 видно, что переход из состояния 1 в состояние 2 возможен при затрате энергии Е, а обратный переход возможен при затрате энергии Е’. Поскольку Е’ > Е, то есть энергетический барьер обратной реакции будет больше, чем прямой, следовательно скорость обратной реакции будет меньше скорости прямой.
В задачу химической кинетики входит найти способы уменьшения энергетического барьера, энергии активации, для увеличения скорости. Одним из таких способов является применение катализатора.
При осуществлении реакции в прямом направлении выделяется количество энергии 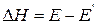 , а в обратном направлении затрачивается такое же количество энергии, что выделяется в прямом.
, а в обратном направлении затрачивается такое же количество энергии, что выделяется в прямом.
Уравнение (5) легко проинтегрировать. Считая, что 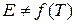 , получим
, получим
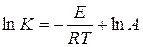
где lnA – константа интегрирования.
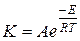
Отсюда видно, что величинами, характеризующими реакцию, являются предэкспоненциальный множитель А и энергия активации Е.
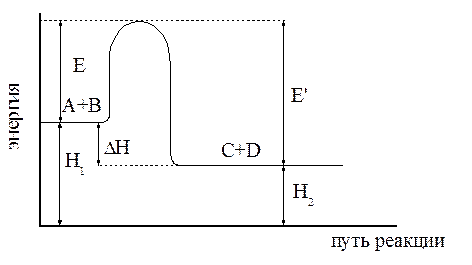
Рисунок – Диаграмма, иллюстрирующая связь Е и 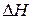 .
.
Поскольку для вступления в химическую реакцию молекулы должны обладать некоторой избыточной энергией (по сравнению со средней величиной) Е (рисунок ), то влияние повышения температуры на рост скорости реакции можно объяснить увеличением числа частиц, обладающих этим избытком энергии.
Обратимся к рисунку , на нем изображена зависимость величины 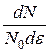 от энергии, так называемая кривая распределения молекул по энергиям. Где dN – число молекул, обладающих энергиями от
от энергии, так называемая кривая распределения молекул по энергиям. Где dN – число молекул, обладающих энергиями от 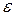 до
до 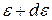 ; N0 – общее число молекул. Пусть
; N0 – общее число молекул. Пусть 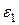 - энергия, превышающая среднюю на энергию активации.
- энергия, превышающая среднюю на энергию активации.
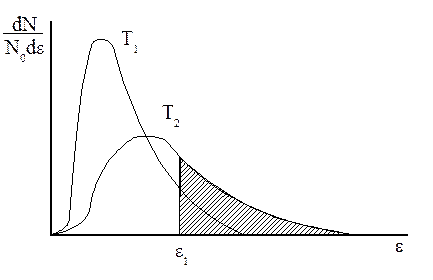
Рисунок – Кривая распределения молекул по энергиям.
Площадь под кривой правее абсциссы 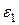 , ограниченная кривой и осью абсцисс, определяет собой долю молекул, обладающих энергией, превышающей
, ограниченная кривой и осью абсцисс, определяет собой долю молекул, обладающих энергией, превышающей 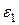 . С повышением температуры (Т2 >Т1) кривая сдвигается вправо, и эта доля молекул быстро возрастает.
. С повышением температуры (Т2 >Т1) кривая сдвигается вправо, и эта доля молекул быстро возрастает.
Величину энергии активации можно определить двумя методами. Первый метод – графический, с использованием уравнения Аррениуса в виде ( ):
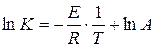
Если построить график зависимости экспериментальных величин от 1/Т, то получим прямую. По оси ординат отсекается отрезок, равный lnA. Тангенс угла наклона на кривой равен 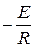 .
.
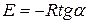

Рисунок
Второй метод – измеряется скорость этой реакции при двух температурах. Тогда из уравнения (5) получим:
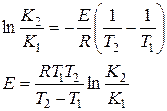
Постоянной энергия активации может быть только в простых реакциях. Для сложных реакций величина «Е» является переменной и не имеет такого простого физического смысла, как в случае простых реакций. Тем не менее и в этом случае принято величину «Е» называть энергией активации, но определяют ее из дифференциального уравнения Аррениуса 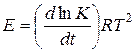 , используя зависимость
, используя зависимость 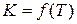 .
.
Дата добавления: 2016-06-22; просмотров: 2765;











