Основные свойства пар сил.

Свойство I. Действие пары сил на тело не изменится от перено­са её в любое положение в одной плоскости.

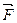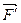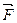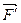Пусть задана пара сил ( , ), действующая в плоскости черте­жа (рис.3.5). Плечо это пары сил равно h . Перенесем точки приложения сил и в новые положения С и D, взятые на линиях действия этих сил. Через точки С и D проведем произвольно параллельные прямые, расстояния между которыми равно плечу h заданной пары сил. Очевидно, что эти прямые образуют тупые углы с линиями действия сил заданной пары. Прямая СD является биссектрисой этих углов (рис.3.5).

В точках С и D вдоль проведенных ранее параллельных прямых приложим по две равные и противоположно направленные силы, имеющие те же модули, что и заданные силы. В тачке С прикладываем силы и 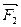, а в точке D - силы 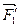и .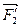

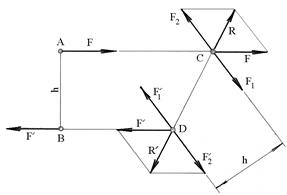
Рис.3.5

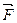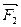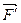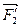Пользуясь правилом параллелограмма, сложим геометрически силы и , приложенные в точке С, а также силы и , приложенные соответственно в точке D . Равнодействующие 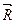и 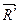указанных сил (рис.3.5) равны по величине и направлены вдоль прямой CD в противоположные стороны. Известно, что такие силы взаимно уравновешиваются и могут быть сняты с тела без нарушения его состояния равновесия или дви­жения. Оставшиеся силы и 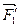, приложенные в точках С и D сос­тавляют новую пару сил, полученную переносом заданной пары сил в новое положение при сохранении модулей сил и плеча пары.

Свойство 2. Действие пары сил на тело не изменится, если пере­нести эту пару в плоскость, параллельную плоскости её действия.

Пусть пара сил ( 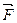, 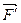), имеющая плечо h, действует в плоскос­ти П₁ (рис.3.6). Возьмем плоскость П₂, расположенную параллельно плоскости П₁ на произвольном от неё расстоянии и из точек приложе­ния сил заданной пары проведем перпендикуляры к плоскости П₂, которые пересекают эту плоскость в точках С и D . Так как прямые ВС и АD одновременно перпендикулярны к плоскостям П₁ и П₂, то четы­рехугольник ABCD является прямоугольником. Следовательно CD = АВ = h .

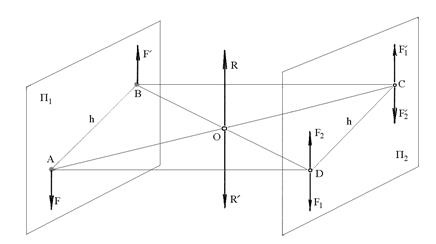
Рис.3.6

Приложим в точках С и D плоскости П₂ по две взаимно уравновешенные силы, линии действия которых перпендикулярны отрезку CD, т.е. силы и 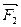в точке С и силы 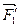и 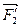в точке D. Эти силы параллель­ны силам заданной пары, а их модули равны модулям сил заданной пары.

Рассмотрим силы 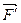и 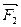. Эти силы равны по модулю, параллель­ны и направлены в одну сторону. Заменим их действие силой 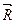, при­ложенной в точке пересечения диагоналей прямоугольника ABCD , на­правленной параллельно указанным силам в ту же сторону и равной их алгебраической сумме, т.е. = + .

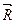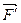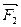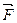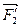Аналогично силы и приводятся к равнодействующей 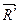, приложенной в точке О, направленной параллельно этим силам в ту же сторону и равной их алгебраической сумме, т.е. = +

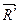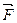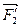
Полученные силы 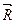и 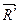взаимно уравновешиваются так как они равны по модулю, приложены в одной точке О и направлены вдоль общей прямой в противоположные стороны.

В результате на тело остаются действовать силы и 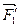, расположенные в плоско-сти П₂ и образующие пару одинаковую с задан­ной парой сил ( 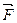, 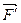). Следовательно, любая пара сил может быть пе­ренесена в параллельную ей плоскость.

Свойство 3. Две пары сил, моменты которых равны и направления вращения совпадают, статически эквивалентны.

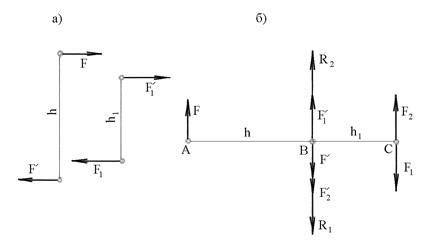
Рис.3.7

Эквивалентные пары оказывают одинаковые воздействия на тела, к которым они приложены.

Рассмотрим две пары сил: ( 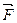, 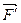) и ( , 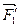) , действующие в одной плоскости и имеющие одинаковые моменты и направления вращения (рис.3.7,а).

Пусть плечо первой пары сил равно h , а плечо второй – h₁ . Тогда их моменты будут равны:

т( 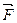, 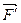)= 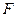∙ h и т ( , 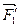) = 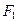∙ h₁

Так как по условию, т( 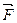, 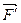)= т ( , 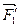) , то

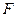∙ h= 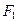∙ h₁ (3.7)

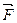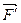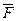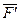Пользуясь первым свойством пар, повернем пару сил ( , )против часовой стрелки в плоскости действия этой пары так, чтобы её составляющие расположились вертикально, т.е. силы и приложим в точках А и В соответственно (рис.3.7,б). На продолжении прямой АВ, отложим отрезок ВС численно равный плечу h₁ пары сил ( , 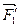) и в точках В и С перпендикуляр­но к этой прямой приложим по две равные и противоположно направ­ленные силы 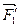, 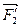и , , 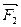которые взаимно уравновешиваются.

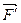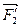Силы и , приложенные в точке В и направленные вдоль общей прямой в одну сторону, приводятся к равнодействующей 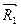, совпадающей по направлению с составляющими силами и численно рав­ной: .

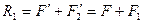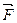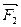Силы и , приложены соответственно в точках А и С дей­ствуют в одну сторону вдоль параллельных прямых. Они приводятся к равнодействующей 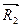, направленной в ту же сторону, равной по мо­дулю их алгебраической сумме 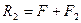, приложенной в точке, которая делит расстояние АС на отрезки, обратно пропорциональные этим силам. Обозначим точку приложения 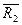буквой B₁ и запишем от­ношение отрезков, на которые сила 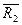делит расстояние АС:

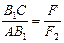(3.8)

Из равенства (3.7) следует:

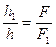, но 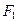= 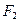, h₁ = ВС и h = АВ. Тогда равенство (3.8) принимает вид:

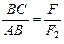(3.9)

Сопоставляя выражения (3.8) и (3.9), легко установить, что точки В и B₁ совпадают.

Таким образом, равнодействующие рассмотренных выше сил прило­жены в точке В, направлены вдоль общей прямой в противоположные стороны и равны по модулю. Такие силы взаимно уравновешиваются.

Оставшиеся силы и 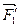образуют пару, результат действия которой равен результату действия пары сил ( , 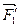),т.е. заданные пары ста­тически эквивалентны.

Из рассмотренного свойства пар вытекают два важных для прак­тики следствия:

а) Действие любой пары сил на тело можно заменить действием другой пары сил, статически ей эквивалентной.

б) При переносе пары сил в плоскости (или в другую плоскость ей параллельную) можно произвольно изменять модуль сил и её плечо при условии, что момент пары остается неизменным по величине и знаку.

3.4. Теорема о сложении пар.