Выражение магнитного потока через векторный потенциал

Установим связь между магнитным потоком Ф сквозь некоторую поверхность s и векторным потенциалом 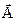магнитного поля. Имеем (3.1)

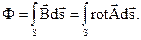
Согласно теореме Стокса последнее выражение можно переписать в виде:

(3.10)

Таким образом, магнитный поток сквозь поверхность s равен линейному интегралу векторного потенциала по замкнутому контуру, ограничивающему эту поверхность.

Граничные условия

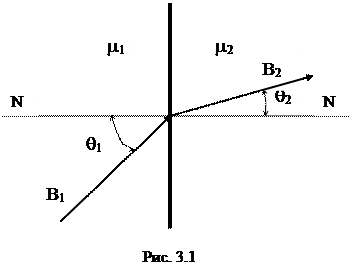На поверхности раздела двух сред с различными магнитными проницаемостями (рис. 3.1) равны между собой касательные составляющие магнитного поля

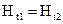(3.11)

и нормальные составляющие магнитной индукции

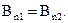(3.12)

Здесь индекс 1 относится к первой среде, а индекс 2 – ко второй.

Условия (3.11) и (3.12) можно представить и в таком виде

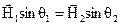и .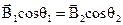

Из данных граничных условий можно получить еще одно условие - условие преломления линий поля при переходе их из одной среды в другую:

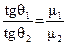, (3.13)

где q₁ и q₂ - углы между вектором магнитной индукции (или напряженности) и нормалями к границе раздела сред.

При этом, если вектор напряженности перпендикулярен к границе раздела, то магнитная индукция не меняется при переходе из одной среды в другую, а напряженность поля меняется скачком.

Большое практическое значение имеет вопрос о характере магнитного поля в воздухе около поверхностей стальных частей различных электротехнических устройств. Магнитные проницаемости ферромагнитной среды и воздуха сильно разнятся между собой. Если магнитные силовые линии выходят из стали (например, с m₁ = 1000m₀) в воздух (m₂ = m₀), то, как следует из уравнения (3.13), угол q₂ будет много меньше угла q₁. Практически можно считать, что линии магнитной индукции в воздухе нормальны к поверхностям тел из ферромагнитных материалов.