Конечные поля многочленов.

Возьмем в кольце многочленов Z_p[x] некоторый неприводимый многочлен f(x)=a_kx^k + … + a₁x + a₀ и построим полную систему наименьших вычетов по модулю f(x) так же, как строили полную систему наименьших неотрицательных вычетов в Z. В эту систему войдут все многочлены из Z_p[x], чья степень меньше k, а таких ровно p^k штук. Получившееся множество вместе с операциями сложения и умножения полиномов с коэффициентами из Z_p по модулю f(x) обозначим как Z_p[x]\f(x). Эта конструкция будет полем мощности p^k, в котором единичным элементом является 1, а нулевым – 0.

В дальнейшем будем обозначать Z_p[x]\f(x) как GF(p^k) (поле Галуа).

Заметим, что GF(p^α) имеет характеристику p, и GF(p) (то есть Z_p) является подполем GF(p^α) для соответствующего p.

Каждый ненулевой элемент поля обратим, и обратный элемент можно найти с помощью расширенного алгоритма Евклида.

Пример.

Построим в Z₂[x] поле GF(2³)=Z₂[x]\f(x), где f(x)=x³+x²+1 – неприводимый многочлен.

GF(2³)={0, 1, x, x+1, x², x²+1, x²+x, x²+x+1}. Мощность построенного множества составляет 2³=8 элементов.

Продемонстрируем процедуры сложения, умножения многочленов и отыскание обратного элемента в Z₂[x]\f(x) на примере:

(x+1)+(x²+x+1)= x².

(x+1)·(x²+x+1)=(x³+x²+x+x²+x+1) mod f(x) = (x³+1) mod f(x) = x².

Отыщем обратный к (x+1) по модулю f(x):

x³+x²+1=x²(x+1)+1 1=f(x)—x²(x+1) (x+1)^-1=(—1 mod 2) x² =x².

Проверка: x²(x+1)mod f(x)=1. Решение верно.

Поскольку GF(p^α) является конечным полем, то, как известно из алгебры, мультипликативная группа его ненулевых элементов является циклической, а значит в нем существует порождающий элемент. Если многочлен f(x) степени m неприводим, и порождающим элементом мультипликативной группы ненулевых элементов поля Z_p[x]\f(x) является многочлен g(x)=x, то f(x) называют примитивным многочленом.

Например, нетрудно проверить, что многочлены x³+x²+1 и x³+x+1 являются примитивными над Z₂.

Теорема 1

Неприводимый многочлен f(x) из Z_p[x] степени m примитивен 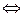f(x)\(x^k—1) для всех k ≥ p^m—1.

Теорема 2

Для любого m≥1 существует φ(p^m—1)/m примитивных многочленов степени m над полем Z_p.

Заметим, что не существует эффективного детерминированного алгоритма нахождения примитивных многочленов. Проще всего генерировать многочлен заданной степени случайным образом и проверять, не является ли он примитивным, например, с помощью критерия Эйзенштейна.

Для конечных полей многочленов, так же как и для Z_p, определено понятие дискретного логарифма.