Отражение и поляризация фотонов
Поскольку фотон вращается относительно своей оси и движется поступательно, то такое движение называется плоскопараллельным, а плоскость вращения – плоскостью поляризации. Спин фотона равен постоянной Планка 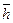 и направлен вдоль оси его вращения перпендикулярно направлению его движения (рис. 16). Тогда упрощенная модель правоциркулярного фотона будет такой, как показана на рис. 23, а, левоциркулярного – на рис. 23, b.
и направлен вдоль оси его вращения перпендикулярно направлению его движения (рис. 16). Тогда упрощенная модель правоциркулярного фотона будет такой, как показана на рис. 23, а, левоциркулярного – на рис. 23, b.
Обратим внимание на четкость смыла, давно введённых понятий правоциркулярной (рис. 23, а) левоциркулярной (рис. 23, b) поляризации фотонов. Важно запомнить правило направления вектора 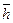 . Оно определяется так, что при виде с острия вектора
. Оно определяется так, что при виде с острия вектора 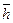 вращение должно быть направлено против хода часовой стрелки.
вращение должно быть направлено против хода часовой стрелки.
Мы уже показали, что движение центра масс такой модели описывают уравнения (70) и (71), а изменение скорости центра масс фотона описывается уравнением (73).
Для анализа процесса отражения фотона необходимо знать закономерность изменения направления вектора скорости центра масс фотона (73) перед отражением. Она представлена на рис. 23, с).
Угол 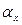 между направлением вектора скорости
между направлением вектора скорости 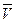 центра масс фотона и осью ОХ (рис. 23, с) определяется по формуле
центра масс фотона и осью ОХ (рис. 23, с) определяется по формуле
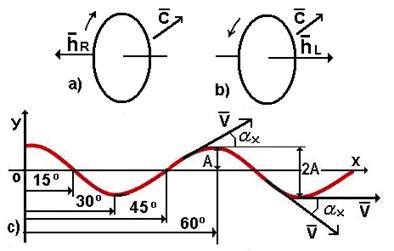
Рис. 23. Упрощенные схемы:
а) модели фотонов с правоциркулярной; b) левоциркулярной
поляризациями; с) закономерность изменения скорости V
центра масс фотона
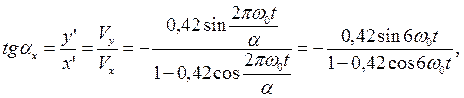 (94)
(94)
где 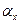 - угол наклона результирующего вектора скорости
- угол наклона результирующего вектора скорости 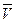 центра масс фотона к оси ОХ;
центра масс фотона к оси ОХ; 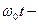 угол поворота центра масс одного магнитного поля фотона (рис. 15, и 16) относительно центра масс фотона;
угол поворота центра масс одного магнитного поля фотона (рис. 15, и 16) относительно центра масс фотона; 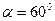 - угол, определяющий количество магнитных полей фотона, замкнутых друг с другом по круговому контуру.
- угол, определяющий количество магнитных полей фотона, замкнутых друг с другом по круговому контуру.
Центр масс фотона находится на гребне волны при 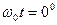 и
и 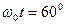 , и - в яме волны при
, и - в яме волны при 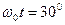 и
и 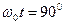 (рис. 23, с). Поскольку модель фотона магнитная, то он легко деформируется при встрече с препятствием. При этом, в момент отражения центр масс фотона находится преимущественно на гребне или в яме волны, то есть при
(рис. 23, с). Поскольку модель фотона магнитная, то он легко деформируется при встрече с препятствием. При этом, в момент отражения центр масс фотона находится преимущественно на гребне или в яме волны, то есть при 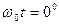 и
и 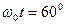 или при
или при 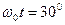 и
и 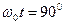 .
.
Для всех этих случаев формула (94) даёт один результат 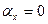 . То есть в момент отражения фотона отсутствует поперечная составляющая импульса
. То есть в момент отражения фотона отсутствует поперечная составляющая импульса 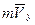 .
.
А теперь проанализируем процесс поляризации фотонов при отражении. Из рис. 24 следует, что плоскость падения 2 луча 1, состоящего из фотонов с разной поляризацией, и плоскость его отражения 4 должны совпадать независимо от ориентации плоскостей фотонов с правоциркулярной и левоциркулярной поляризациями перед отражением.
Отсутствие поперечной составляющей импульса 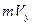 у всех отражающихся фотонов должно приводить их к поляризации в момент отражения. Вполне естественно, что в неполяризованном луче плоскости вращения фотонов будут параллельны направлению движения луча света и ориентированы произвольно (рис. 24, падающий луч 1). В дальнейшем мы будем характеризовать поляризацию фотонов плоскостями их вращения. Поляризация отраженных фотонов была открыта Этьен Малюсом в 1808 г.
у всех отражающихся фотонов должно приводить их к поляризации в момент отражения. Вполне естественно, что в неполяризованном луче плоскости вращения фотонов будут параллельны направлению движения луча света и ориентированы произвольно (рис. 24, падающий луч 1). В дальнейшем мы будем характеризовать поляризацию фотонов плоскостями их вращения. Поляризация отраженных фотонов была открыта Этьен Малюсом в 1808 г.
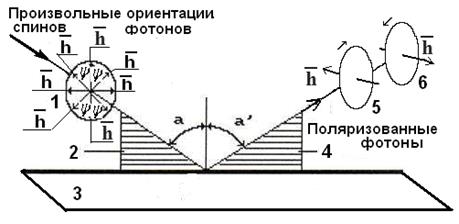
Рис. 24. Схема поляризации отраженных фотонов:
1 – падающий луч; 2 – плоскость падения; 3-отражающая поверхность;
4 – плоскость отражения; 5 и 6 – отраженные фотоны
Возникает вопрос: все ли фотоны поляризуются после отражения так, что плоскость их поляризации совпадает с плоскостью падения 2 лучей? Ответ на этот вопрос дал Френель (рис. 24). Он установил, что фотоны, поляризованные в плоскости падения 2 и перпендикулярно ей, после отражения не меняют направление своих плоскостей поляризации. Если же плоскости поляризации фотонов не параллельны и не перпендикулярны плоскости падения 2, то отражение таких фотонов сопровождается поворотом плоскостей их поляризации в таком направлении, что все они оказываются поляризованными в плоскости отражения 4, совпадающей с плоскостью падения 2. Из этого следует, что в падающем луче света направление своей плоскости поляризации после отражения изменяют лишь те фотоны, у которых угол 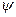 между плоскостью падения 2 луча 1 и плоскостью поляризации находится в интервале
между плоскостью падения 2 луча 1 и плоскостью поляризации находится в интервале 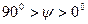 . Те же фотоны, у которых плоскость поляризации перпендикулярна (
. Те же фотоны, у которых плоскость поляризации перпендикулярна ( 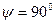 ) плоскости падения 2 или совпадает с ней (
) плоскости падения 2 или совпадает с ней ( 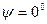 ), отражаются, не меняя ориентации своей плоскости поляризации.
), отражаются, не меняя ориентации своей плоскости поляризации.
Из описания Френеля следует, что большая часть фотонов поляризуется в плоскости отражения 4 (рис. 24) и меньшая часть - в плоскости, перпендикулярной плоскости отражения. Схематически это можно показать в виде позиций 5 и 6 поляризованных фотонов (рис. 24).
Таким образом, если плоскость поляризации падающего фотона (рис. 24) перпендикулярна плоскости падения 2 или лежит в ней, то плоскость 3, на которую падает фотон, не меняет направление плоскости его поляризации. Если же плоскость поляризации падающего фотона не перпендикулярна плоскости падения 2, то отражающая плоскость 3 изменяет её направление так, что она становится параллельной плоскости отражения 4.
Таким образом, в отраженном луче большая часть фотонов поляризована в плоскости отражения 4 и меньшая часть в плоскости, перпендикулярной плоскости отражения. Возникает вопрос: почему фотоны ведут себя так? Если плоскость поляризации фотона не перпендикулярна плоскости падения 2, то все фотоны начинают контактировать с отражающей плоскостью 3 одним (из шести) магнитных полюсов, что облегчает процесс поворота их плоскостей поляризации. При этом, если угол падения равен или близок к 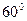 , то скорость центра масс фотона равна 1,4С (рис. 22, а). Это главный факт существования угла Брюстера (рис. 26, зависимость 3).
, то скорость центра масс фотона равна 1,4С (рис. 22, а). Это главный факт существования угла Брюстера (рис. 26, зависимость 3).
Когда плоскость поляризации фотона перпендикулярна плоскости падения 2, то фотон, сближаясь с отражающей плоскостью 3, контактирует с ней в основном двумя магнитными полями, что увеличивает устойчивость процесса контакта и затрудняет поворот плоскости поляризации фотона при его отражении (рис. 24).
Теперь нам необходимо запомнить ориентиры поляризации фотонов. Первый и главный – плоскость вращения фотона совпадает с плоскостью поляризации и c направлением движения фотонов. Второй - направление спина 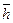 фотона. Он всегда направлен перпендикулярно направлению движения фотона, плоскости его вращения и плоскости поляризации. Из этого следует, что если на схеме показана траектория движения фотона (луча света), то плоскость поляризации фотона параллельна этой траектории, а спин
фотона. Он всегда направлен перпендикулярно направлению движения фотона, плоскости его вращения и плоскости поляризации. Из этого следует, что если на схеме показана траектория движения фотона (луча света), то плоскость поляризации фотона параллельна этой траектории, а спин 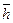 - перпендикулярен ей.
- перпендикулярен ей.
На рис. 25, b представлена схема очень важного опыта С.И. Вавилова, доказавшего поляризацию отраженных фотонов. Вначале (рис. 25, а) неполяризованный лучь света 1, направляется в сосуд 2 с водой, взмученной каплей молока. Пройдя через сосуд, он высвечивается на экране 3 в неполярзованном состоянии 4.
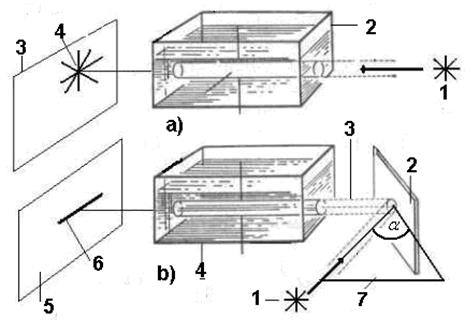
Рис. 25: а) через сосуд 2 с водой, взмученной каплей молока, проходит неполяризованный луч света 1 и на экране 3 высвечивается в таком же неполяризованном состоянии 4; b) луч света 1, отразившись от плоскости 2 под углом 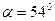 , направляется 3 через тот же сосуд 4 и на экране 5 высвечивается в состоянии 6, поляризованном в
, направляется 3 через тот же сосуд 4 и на экране 5 высвечивается в состоянии 6, поляризованном в
плоскости падения 7
Если же через этот же сосуд направить луч света 1 (рис 25, b) отраженный от плоскости 2 под углом, примерно 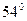 , то рассеяние света наблюдается в основном в горизонтальной плоскости 7, а при виде на сосуд сверху, рассеянный свет очень слаб или почти не виден.
, то рассеяние света наблюдается в основном в горизонтальной плоскости 7, а при виде на сосуд сверху, рассеянный свет очень слаб или почти не виден.
Таким образом, луч света, проходящий через сосуд без предварительного отражения (рис. 25, а), рассеивается во всех направлениях, что указывает на то, что фотоны в нём сохраняют исходную поляризацию 1. Если же в сосуд (рис. 25, b) направить такой же 1, но отраженный луч 3, то он, отражаясь от плоскости 2, поляризуется и, проходя через сосуд, рассеивается в основном в горизонтальной плоскости 7 и высвечивается на экране 5 в виде горизонтальной полосы 6. Это является доказательством того, что отраженный луч поляризован в основном в плоскости падения 7 (рис. 25, b), как это показано 6 на экране 5.
Простой опыт, проведённый С. И. Вавиловым, является косвенным доказательством отсутствия поперечной составляющей импульса у отраженных фотонов (94). Из этого также следует, что независимо от направления плоскостей поляризации падающих фотонов плоскость поляризации 6 отражённых фотонов 3 совпадает с плоскостью падения 7. Попутно отметим, что в этом простом опыте отражена физическая суть работы телевизоров, интернета и мобильных телефонов.
Далее, необходимо знать детали процесса отражения поляризованных фотонов. На рис. 26 показаны зависимости коэффициента отражения фотонов с разной поляризацией на границе воздух-стекло.
Обратим внимание на то, что при совпадении плоскостей падения, отражения и поляризации фотонов коэффициент отражения при угле падения, близком к 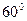 , приближается к нулю (рис. 26, зависимость 3). Угол этот называется углом Брюстера. Его величина зависит от показателя преломления
, приближается к нулю (рис. 26, зависимость 3). Угол этот называется углом Брюстера. Его величина зависит от показателя преломления 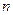 . Если
. Если 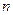 равно 1,4; 1,5; 1,6 или 2,0, то угол Брюстера составляет соответственно
равно 1,4; 1,5; 1,6 или 2,0, то угол Брюстера составляет соответственно 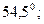
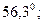
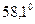 и
и 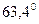 .
.
Мы уже описали причину такого поведения фотонов. При угле падения, близком к 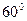 , центр масс фотона, начинающего контактировать с отражающей плоскостью, на гребне волны и его скорость равна 1,42 С (рис. 20, а), поэтому он и проходит через материал отражающей плоскости или поглощается электронами атомов этого материала (рис. 26, зависимость 3).
, центр масс фотона, начинающего контактировать с отражающей плоскостью, на гребне волны и его скорость равна 1,42 С (рис. 20, а), поэтому он и проходит через материал отражающей плоскости или поглощается электронами атомов этого материала (рис. 26, зависимость 3).
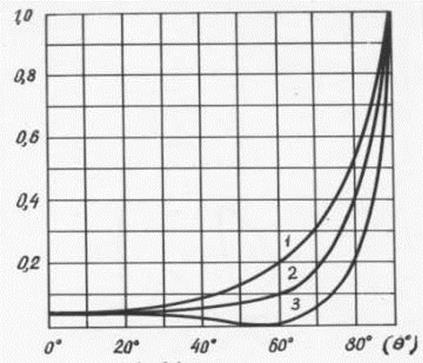
Рис. 26. Зависимость коэффициента отражения фотонов от границы воздух – стекло от угла падения 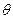 при разной их поляризации:
при разной их поляризации:
1 – плоскости падения фотонов и поляризации перпендикулярны;
2 – неполяризованный луч; 3 – плоскости падения, поляризации и отражения фотонов совпадают
Дифракция фотонов
Дифракция фотонов рождает картины, подобные картинам, возникающим при взаимодействии волн. Поэтому дифракция фотонов считается главным доказательством того, что модель фотона - волна.
Однако, энергия фотона, определяемая по формуле 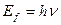 , убедительно доказывает, что фотон – корпускула. Анализ существующих математических моделей, описывающих поведение фотона, как мы уже показали, подтверждает этот факт.
, убедительно доказывает, что фотон – корпускула. Анализ существующих математических моделей, описывающих поведение фотона, как мы уже показали, подтверждает этот факт.
Сейчас мы увидим, как дифракция фотонов управляется процессом взаимодействия их ротационных полей, которые формируются их спинами 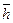 .
.
Главный факт, который мы должны учитывать при анализе процессов дифракции фотонов – взаимодействие их спинов. Чтобы понять суть этого взаимодействия, проанализируем взаимодействие осей вращения (эквивалентно спинов) гироскопа. В качестве гироскопа можно представить вращающийся волчок (рис. 27).
Известно, что если подействовать на ось быстро вращающегося волчка, то она начнет описывать коническую поверхность и у волчка появляются два вращения: одно относительно оси его симметрии (рис. 27, а) и второе – вращение оси волчка относительно вертикали, называемое прецессией волчка (рис. 27, b). Однако прецессионное вращение волчка оказывается недолгим. Его ось вращения быстро возвращается в вертикальное положение. Процессом возврата оси волчка из наклонного в вертикальное положение управляет гироскопический момент 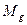 , определяемый по формуле
, определяемый по формуле
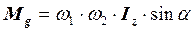 , (95)
, (95)
где 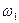 - угловая скорость вращения волчка относительно своей оси;
- угловая скорость вращения волчка относительно своей оси; 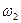 - угловая скорость вращения оси волчка относительно вертикали (угловая скорость прецессии);
- угловая скорость вращения оси волчка относительно вертикали (угловая скорость прецессии); 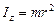 - момент инерции волчка относительно оси вращения
- момент инерции волчка относительно оси вращения 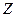 ;
; 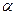 - угол между векторами
- угол между векторами 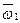 и
и 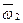 .
.
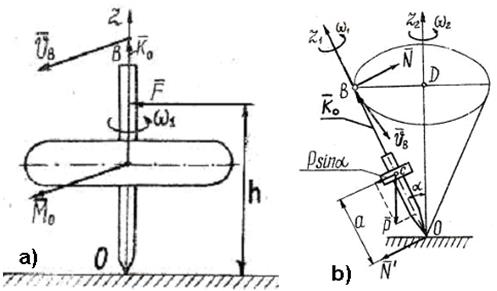
Рис. 27: а) волчок; b) прецессия волчка
Гироскопический момент – следствие реакции поверхности, которой касается вращающаяся ось волчка. Главное следствие описанного явления – стремление волчка иметь одну ось вращения. Оно подтверждается поведением свободного гироскопа, у которого силы, действующие на ось, близки к нулю. Поэтому он имеет одну ось вращения, направление которой в пространстве не меняется при любом повороте корпуса, в котором крепится гироскоп.
А теперь обратим внимание на формулу (95). При совпадении оси вращения гироскопа и оси прецессии 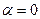 ,
, 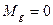 ,
, 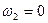 .
. 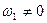 (рис. 27, b). Поскольку момент инерции гироскопа равен
(рис. 27, b). Поскольку момент инерции гироскопа равен 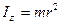 , то в формуле гироскопического момента (95) остаётся выражение
, то в формуле гироскопического момента (95) остаётся выражение 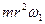 . Это и есть спин
. Это и есть спин 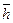 гироскопа – величина векторная. У фотона она равна постоянной Планка
гироскопа – величина векторная. У фотона она равна постоянной Планка 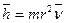 , поэтому фотон также обладает гироскопическими свойствами, но ось его вращения не имеет какой – либо материальной основы.
, поэтому фотон также обладает гироскопическими свойствами, но ось его вращения не имеет какой – либо материальной основы.
Тем не менее, в окружающем его пространстве формируется ротационное поле, носителем которого является, по-видимому, субстанция, называемая эфиром, из которого формируется магнитное поле вокруг проводника с током (рис. 14). В последние годы такое поле называют торсионным. Поскольку этот термин ещё не закрепился, то нам представляется, что понятие «ротационное поле» точнее отражает то, что формируется вблизи вращающегося тела или частицы. Источником формирования такого поля является процесс вращения, который характеризуется величиной, названной спином 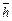 .
.
У фотона, электрона, да и у других частиц, эту функцию выполняет постоянная Планка. Поскольку спин 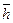 фотона перпендикулярен плоскости его вращения и направлению движения, то возникает вопрос: как будут взаимодействовать друг с другом два фотона, если оси их вращения совпадут, и спины будут направлены в одну сторону? В этом случае плоскости их вращения будут параллельны, и они будут иметь одинаковую циркулярную поляризацию (рис. 28, а).
фотона перпендикулярен плоскости его вращения и направлению движения, то возникает вопрос: как будут взаимодействовать друг с другом два фотона, если оси их вращения совпадут, и спины будут направлены в одну сторону? В этом случае плоскости их вращения будут параллельны, и они будут иметь одинаковую циркулярную поляризацию (рис. 28, а).
Экспериментально установлено, что два параллельных луча света с одинаковой циркулярной поляризацией, движущиеся на расстоянии 0,5 мм друг от друга, притягиваются (рис. 28, а), а при противоположной циркулярной поляризации – отталкиваются (рис. 28, b). Отмечается, что сила взаимодействия между ними квадратично зависит от расстояния.
Вот что писал об этом Френель в 1816 г. «Поляризованные световые волны взаимодействуют, как силы, перпендикулярные к лучам». Далее он отметил, что лучи, поляризованные во взаимно перпендикулярных плоскостях, не оказывают друг на друга такого влияния, которое наблюдается у лучей, поляризованных в одном направлении. Это очень важное наблюдение. Оно проясняет картину взаимодействия единичных фотонов (рис. 28). Модель фотона позволяет нам понять причину сближения и отталкивания фотонов при разной циркулярной поляризации. Когда направления циркулярной поляризации совпадают, то, видимо, совпадают и направления эфинрых вихрей, формируемых вращающимися фотонами, и они сближаются (рис. 28, а).

Рис. 28. Схема взаимодействия лучей фотонов:
а) с одинаковой циркулярной поляризацией;
b) с противоположной циркулярной поляризацией
Когда же направления циркулярной поляризации противоположны, то вращение эфирных вихрей противоположно и фотоны, формирующие их, удаляются друг от друга (рис. 28, b).
Нетрудно видеть, как будут вести себя два фотона с одинаковой циркулярной поляризацией, если линии их движения будут пересекаться (рис. 29).
Если спины 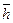 фотонов будут взаимно перпендикулярны или будут близки к перпендикулярному состоянию, то, согласно Френелю, они не будут взаимодействовать. Если же угол между направлениями спинов будет острый, то есть все основания полагать, что при сближении их поведение будет подобно поведению волчка, имеющего две оси вращения (рис. 27, b). Как и волчок, фотоны будут стремиться сделать свои оси вращения соосными, а спины
фотонов будут взаимно перпендикулярны или будут близки к перпендикулярному состоянию, то, согласно Френелю, они не будут взаимодействовать. Если же угол между направлениями спинов будет острый, то есть все основания полагать, что при сближении их поведение будет подобно поведению волчка, имеющего две оси вращения (рис. 27, b). Как и волчок, фотоны будут стремиться сделать свои оси вращения соосными, а спины 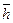 - направленными в одну сторону (рис. 29).
- направленными в одну сторону (рис. 29).
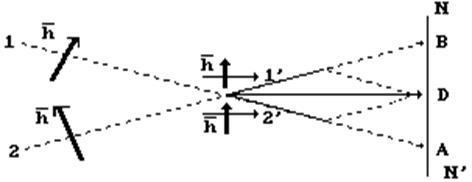
Рис. 29. Схема изменения направления движения
фотонов с синхронизированной частотой и
одинаковой циркулярной поляризацией
Поскольку параметры их ротационных полей определяют их постоянные Планка, а они у всех фотонов одинаковые, то, взаимодействуя друг с другом, они будут стремиться совместить свои оси вращения. Результирующая ось вращения фотонов изменит направления их движения (рис. 29). Если до встречи они двигались по траекториям 1 и 2, в которых лежат плоскости их поляризации, то после взаимодействия спинов  они начнут двигаться по траекториям 1’ и 2’ и окажутся на экране не в точках А и В, а в точке D. Этому будет способствовать и эффект сближения траекторий фотонов с одинаковой циркулярной поляризацией (рис. 28, а).
они начнут двигаться по траекториям 1’ и 2’ и окажутся на экране не в точках А и В, а в точке D. Этому будет способствовать и эффект сближения траекторий фотонов с одинаковой циркулярной поляризацией (рис. 28, а).
Итак, изложенная нами информация позволяет перейти к анализу явлений дифракции и интерференции фотонов. Сейчас мы увидим, что это одно и то же явление и нет нужды называть его двумя понятиями.
Теперь нам надо описать характеристики объектов, взаимодействуя с которыми, фотоны формируют дифракционные картины. Прежде всего, обратим внимание на дифракционные картины, формируемые фотонами, проходящими через отверстия. На рис. 30, а дифракция Фраунгофера на круглом отверстии диаметром 6 мм, а на рис. 30, b – его же дифракционная картина на прямоугольном отверстии (7х8 мм).
Сразу видно, что главную роль в формировании этих картин играет геометрия контура отверстия. Если контур – окружность, то дифракционная картина состоит из кругов и колец (рис. 30, а). Если же форма контура отверстия прямоугольная, то дифракционная картина состоит из двух серий взаимно перпендикулярных полос (рис. 30, b). Из этого однозначно следует, что главную роль в формировании дифракционных картин играет контур отверстия, а точнее – контур отражения фотонов. Для простоты последующего анализа возьмём круглое отверстие с диаметром 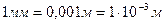 или проволоку с таким же диаметром.
или проволоку с таким же диаметром.
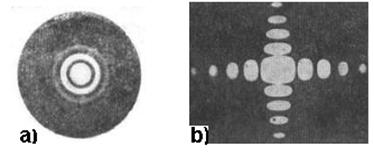
Рис. 30: а) дифракционная картина Фраунгофера на круглом отверстии диаметром 6 мм; b) Фраунгоферова дифракция на квадратном
отверстии (7х8 мм)
Так как длина волны фотонов светового диапазона изменяется от 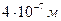 до
до 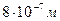 (табл. 2), то в дальнейшем будем использовать среднюю величину
(табл. 2), то в дальнейшем будем использовать среднюю величину 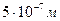 , которая соответствует зелёному фотону. Учитывая, что размер фотона, примерно, в два раза больше его длины волны или радиуса, имеем
, которая соответствует зелёному фотону. Учитывая, что размер фотона, примерно, в два раза больше его длины волны или радиуса, имеем 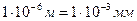 . Из этого следует, что отверстие или провод диаметром 1мм, примерно, в тысячу раз (на три порядка) больше размера одного фотона.
. Из этого следует, что отверстие или провод диаметром 1мм, примерно, в тысячу раз (на три порядка) больше размера одного фотона.
Дифракция фотонов на отверстии образуются в результате пересечения траекторий фотонов, отраженных от кромок О-О отверстия (рис. 31). Кроме того, в процессе отражения они поляризуются (рис. 24).
Если траектории фотонов с разной циркуляционной поляризацией будут пересекаться, то разнонаправленные ротационные поля будут отталкивать их друг от друга (рис. 28, b).
Траектории фотонов 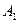 и
и 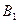 (рис. 31) вначале будут сближаться (1-1’) и (2-2’), а потом расходиться (1’-1’’) и (2’-2’’) и они окажутся на экране NN’ не в точках C и D, а в точках A и B (рис. 31). Если в потоке окажутся фотоны
(рис. 31) вначале будут сближаться (1-1’) и (2-2’), а потом расходиться (1’-1’’) и (2’-2’’) и они окажутся на экране NN’ не в точках C и D, а в точках A и B (рис. 31). Если в потоке окажутся фотоны 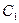 и
и 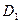 , с одинаковой циркулярной поляризацией, то траектории их движения будут сближаться, и они окажутся на экране не в точках C и D, а в точке Е.
, с одинаковой циркулярной поляризацией, то траектории их движения будут сближаться, и они окажутся на экране не в точках C и D, а в точке Е.
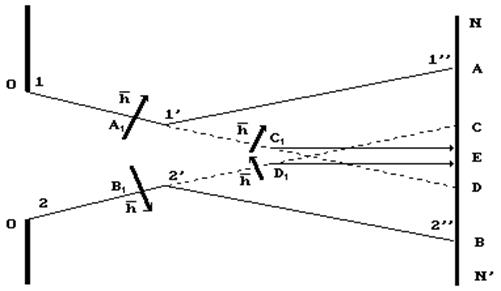
Рис. 31. Схема взаимодействия фотонов с разной и одинаковой циркулярной поляризацией, отражённых от кромок отверстия
Взаимодействие спинов фотонов начинается на расстоянии между ними, примерно, равном 0,5 мм, то есть на расстоянии в 500 раз большем размеров самих фотонов. Эту же величину начала взаимодействия фотонов установил и Френель. Она почти в 500 раз больше размера фотона. Учитывая эту особенность, опишем формирование дифракционной картины за проволокой (рис. 32).
Отметим те важные наблюдения, которые были сделаны Френелем при анализе дифракционной картины за проволокой. Если прикрыть свет, исходящий от одной стороны проволоки, то внутренние каёмки исчезают. Следовательно, для образования каёмок необходимо взаимодействие лучей, идущих с обеих сторон проволоки. Из этого также следует, что каёмки образуются в результате перекрещивания лучей света, идущих от обеих сторон проволоки или, иными словами, в результате пересечения траекторий движения фотонов.
Френель считал, что каёмки снаружи тени образуются скрещиванием лучей, исходящих от светящейся точки и от краёв проволоки, а каёмки внутри тени образуются скрещиванием лучей света, загибающихся около обоих краёв проволоки. Если один край проволоки закрыть, то каёмки исчезают (рис. 32).
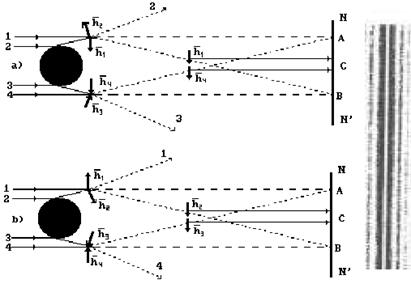
Рис. 32. Схема формирования светлой полосы в центре тени
от проволоки
Френель считал, что результаты его опытов - веское доказательство волновой природы света и ошибочности точки зрения Ньютона о корпускулярной его структуре. Сейчас мы увидим, что ошибался Френель, но не Ньютон.
Фотоны 1 и 4 пролетают вблизи проволоки. Фотоны 2 и 3 отражаются от краёв проволоки (рис. 32). Вполне естественно, что при отражении от проволоки фотоны поляризуются с разной циркулярной поляризацией. Конечно, спины 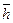 у всех фотонов одинаковые по величине, но, чтобы облегчить анализ их поведения, присвоим им номера. Если спины фотонов 1 и 2
у всех фотонов одинаковые по величине, но, чтобы облегчить анализ их поведения, присвоим им номера. Если спины фотонов 1 и 2 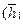 и
и 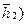 направлены противоположно (рис. 32, а), то их траектории удаляются друг от друга (рис. 28, b). Аналогично ведут себя и фотоны 3 и 4.
направлены противоположно (рис. 32, а), то их траектории удаляются друг от друга (рис. 28, b). Аналогично ведут себя и фотоны 3 и 4.
Поскольку спины фотонов 1 и 4 направлены в одну сторону, то их траектории сближаются (рис. 28, а) и они оказываются не в точках А и В экрана NN’, а в точке С (рис. 32). Аналогично ведут себя фотоны с противоположной циркулярной поляризацией (рис. 32, b). В результате в центре тени от проволоки образуется светлая полоса. Вот что об этом писал О. Френель: «Из опытов, которые я провел, вытекает, что явления дифракции нельзя приписать только лучам, которые касаются тел, и поэтому следует предположить, что бесконечное множество других лучей, отделенных от этих тел заметными интервалами, тем не менее, оказываются повернутыми от своего первоначального направления и также участвуют в образовании каёмок». Описанное при анализе рис. 32, подтверждает это тонкое наблюдение Френеля.
А теперь проанализируем теорию Френеля. Он считал, что при взаимодействии волн света, идущих от точечного источника, с краями проволоки (рис. 32) образуются вторичные волны, которые, пересекаясь, формируют дифракционные картины в тени проволоки. Для теоретического доказательства этой гипотезы он взял крайние точки проволоки в качестве центров и провел из них две окружности с радиусами, отличающимися на половину длины 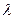 волны света.
волны света.
Свет движется от источника света касается краёв А и В (рис. 33) проволоки, где, по мнению Френеля, формируются вторичные волны, которые распространяются в виде сфер с радиусами 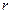 и
и 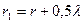 , длина которых отличается на половину длины волны
, длина которых отличается на половину длины волны 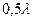 света.
света.
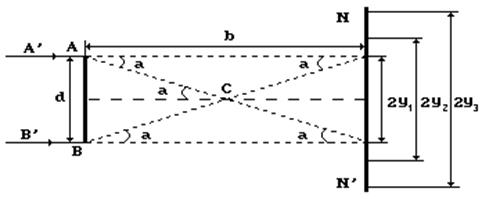
Рис. 33. Схема к анализу теории и эксперимента Френеля
Уравнения световых окружностей он записал так:
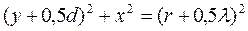 , (96)
, (96)
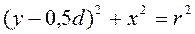 . (97)
. (97)
Совместное решение этих уравнений даёт результат
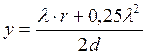 . (98)
. (98)
Пренебрегая квадратом длины волны ввиду того, что величина эта очень маленькая, он получил
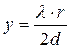 . (99)
. (99)
Следующий шаг Френель делает без каких-либо пояснений. Вместо радиуса сферы 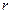 он ставит в уравнение (99) величину
он ставит в уравнение (99) величину 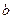 - расстояние от проволоки до экрана
- расстояние от проволоки до экрана 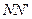 (рис. 33).
(рис. 33).
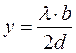 . (100)
. (100)
Чтобы формула (100) давала результат расчета расстояний между тёмными каёмками разных порядков, Френель ввел в неё коэффициент, который принимает значения 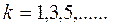 и формула (100) приняла следующий окончательный вид
и формула (100) приняла следующий окончательный вид
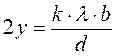 . (101)
. (101)
В табл. 4 приведены экспериментальные данные Френеля и результаты расчета по формуле (101). При этом диаметр проволоки 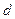 равнялся 1 мм, а длина волны света -
равнялся 1 мм, а длина волны света - 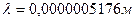
Как видно (табл. 4), сходимость теоретических результатов с экспериментальными данными достаточно хорошая. Это даёт основание считать, что формула Френеля имеет ещё один вывод. Чтобы найти его, преобразуем формулу (101) следующим образом
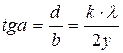 . (102)
. (102)
Таблица 4. Результаты опытов Френеля
| b, м | Порядок каёмки | Теория (м) | Эксперимент (м) |
| 0, 592 | 2-й | 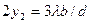 =0,00092 =0,00092
| 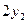 =0,00096 =0,00096
|
| 0,592 | 3-й | 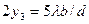 =0,00153 =0,00153
| 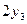 =0,00161 =0,00161
|
| 1,996 | 2-й | 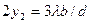 =0,00310 =0,00310
| 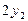 =0,00323 =0,00323
|
| 3,633 | 1-й | 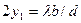 =0,00188 =0,00188
| 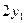 =0,00188 =0,00188
|
Из формулы (102) следует, что 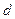 и
и 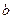 , а также
, а также 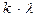 и
и 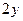 - катеты подобных прямоугольных треугольников (рис. 33, 34). Схема на рис. 34, показывает, что при постоянных значениях
- катеты подобных прямоугольных треугольников (рис. 33, 34). Схема на рис. 34, показывает, что при постоянных значениях 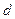 и
и 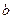 угол
угол 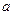 постоянен.
постоянен.
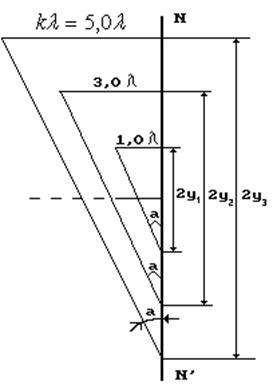
Рис. 34. Схема к анализу закономерности изменения правой части
формулы (102)
Это значит, что числитель 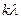 и знаменатель
и знаменатель 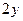 в формуле (102) изменяются пропорционально так, что их отношение остаётся постоянным (рис. 34).
в формуле (102) изменяются пропорционально так, что их отношение остаётся постоянным (рис. 34).
Таким образом, числитель 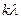 и знаменатель
и знаменатель 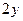 формулы (102) изменяются так, что их отношение остаётся постоянным для всех тёмных каёмок дифракционной картины за проволокой. Величины
формулы (102) изменяются так, что их отношение остаётся постоянным для всех тёмных каёмок дифракционной картины за проволокой. Величины 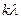 показывают место расположения каёмки на экране NN’ (рис. 34). Таким образом, формулы (100) и (101) Френеля не имеют никакого отношения к волновому распространению света. Они следуют из описанного процесса взаимодействия спинов фотонов, как частиц.
показывают место расположения каёмки на экране NN’ (рис. 34). Таким образом, формулы (100) и (101) Френеля не имеют никакого отношения к волновому распространению света. Они следуют из описанного процесса взаимодействия спинов фотонов, как частиц.
В табл. 5 представлены результаты эксперимента Френеля и дан расчёт тангенса угла 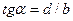 , по величине которого можно судить о небольшой величине угла, под которым фотоны, коснувшись края проволоки, движутся к экрану.
, по величине которого можно судить о небольшой величине угла, под которым фотоны, коснувшись края проволоки, движутся к экрану.
Таблица 5. Результаты экспериментов Френеля
| Величина b, м | Порядок каёмки | Формулы для расчета | 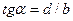
|
| 0,592 | 2-й | 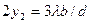
| 0,000845 |
| 0,592 | 3-й | 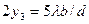
| 0,000845 |
| 1,996 | 2-й | 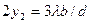
| 0,000250 |
| 3,633 | 1-й | 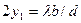
| 0,000138 |
Таким образом, формула (100) Френеля следует из прямоугольного треугольника на рис. 33, который образуется траекториями движения фотонов между препятствием, формирующим дифракционную картину, и экраном.
Поскольку угол 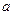 в формуле (102) очень маленький, то при выводе формул можно использовать две тригонометрические функции
в формуле (102) очень маленький, то при выводе формул можно использовать две тригонометрические функции 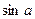 и
и 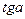 , поэтому надо знать пределы изменения этого угла, при которых допустима такая замена (табл. 6).
, поэтому надо знать пределы изменения этого угла, при которых допустима такая замена (табл. 6).
Таблица 6. Значения углов и тригонометрических функций
Угол 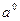
| 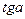
| 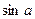
| 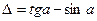
|
| 0,0 | 0,0000 | 0,0000 | 0,0000 |
| 1,0 | 0,0175 | 0,0175 | 0,0000 |
| 2,0 | 0,0349 | 0,0349 | 0,0000 |
| 3,0 | 0,0524 | 0,0523 | 0,0001 |
| 4,0 | 0,0699 | 0,0698 | 0,0001 |
| 5,0 | 0,0875 | 0,0872 | 0,0003 |
Сравнивая таблицы 7 и 8, видим, что самый большой угол 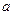 в экспериментах (табл. 5) меньше
в экспериментах (табл. 5) меньше 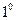 . Следовательно (табл. 6), имеется возможность использовать вместо -
. Следовательно (табл. 6), имеется возможность использовать вместо - 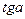 функцию
функцию 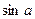 . Необходимость использования гипотенузы прямоугольного треугольника вместо его катетов может возникать при экспериментальных исследованиях. Тогда формуле (102) будут соответствовать схемы, показанные на (рис. 33 и 34).
. Необходимость использования гипотенузы прямоугольного треугольника вместо его катетов может возникать при экспериментальных исследованиях. Тогда формуле (102) будут соответствовать схемы, показанные на (рис. 33 и 34).
Представление о волновой природе света сформировались не только на основании опытов Френеля, но и - Юнга. Самым знаменитым из них является опыт по, так называемой интерференции света за двумя щелями (рис. 35).
Свет проходит через щели А и В и на экране NN’ формируется, как считалось, интерференционная картина, как следствие сложения волн, исходящих из двух щелей. Юнг установил, что расстояния между светлыми полосами рассчитываются по формуле
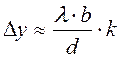 . (103)
. (103)
Аналогичная величина в опыте Френеля с учетом формулы (103) определится так
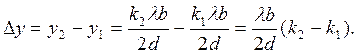 (104)
(104)
В опыте Френеля 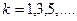 , поэтому
, поэтому 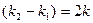 и формула (104) принимает вид формулы Юнга (103). Если величину
и формула (104) принимает вид формулы Юнга (103). Если величину 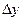 измерять от оси симметрии (рис. 32, 33, 34), то
измерять от оси симметрии (рис. 32, 33, 34), то
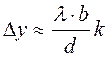 . (105)
. (105)
Формула Френеля (105) для расчета дифракционной картины за проволокой (рис. 32) отличается от формулы Юнга (103) для расчета дифракционной картины за двумя щелями (рис. 35) значением коэффициента 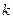 .
.
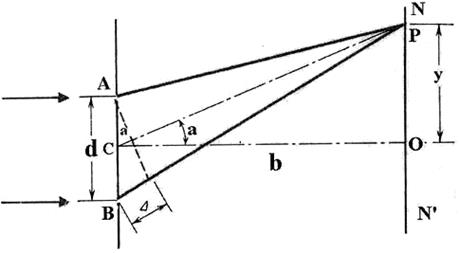
Рис. 35. Схема эксперимента Юнга с двумя щелями
Френель измерял расстояния, как он писал, между темными каёмками с учетом центра картины. Юнг измерял просто расстояния между светлыми каёмками, начиная от центральной светлой полосы. Поскольку явление, формирующее дифракционные картины в обоих случаях одно и тоже, то формула для их расчёта получается одна. Так как в центре картины светлая полоса (рис. 32, b, 35), то коэффициент 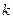 в формуле (103) Юнга принимает значения
в формуле (103) Юнга принимает значения 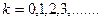 , а в формуле (102) Френеля - значения
, а в формуле (102) Френеля - значения 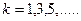 .
.
Юнг установил, что количество интерференционных полос увеличивается с увеличением расстояния от щелей А и В до экрана NN’(рис. 35). Такая закономерность объясняется увеличением количества пересечений траекторий фотонов по мере удаления их от источников поляризации, то есть - от кромок щелей А и В (рис. 35, 36).
 а)
а)
|  b)
b)
|  c)
c)
|
Рис. 36. Схема формирования дифракционных (интерференционных полос) за двумя щелями при разном расстоянии до экрана
Мы привели качественное и, частично, количественное объяснение корпускулярных свойств света при взаимодействии спинов фотонов, проходящих через отверстия и отраженных от кромок проволоки и щелей. Этого достаточно для доказательства формирования дифракционных картин потоками фотонов, спины которых взаимодействуют при пересечении траекторий их движения от краёв отверстий. Поэтому нет нужды вводить понятие интерференция волн.
Конечно, Френель и Юнг не могли предвидеть рождение лазерных технологий не только гражданского, но и военного назначения. Американцы рекламировали свою военную лазерную экспериментальную установку, оборудование которой (конденсаторы и трансформаторы) занимало площадь, равную площади футбольного поля. В 2012г их специалистам впервые было позволено посетить российский город Саров. Корреспонденты поинтересовались, что они хотели бы увидеть в этом, недавно закрытом для иностранцев, городе? Ответ был краток: «Лазеры».
Весной 2013г Интернет раскрыл причину этого интереса. Американский эсминец, шедший по Чёрному морю на помощь Украине в освобождении Крыма, был встречен российским самолётом. После облёта эсминца на значительном расстоянии от него, операторы всех электронных систем эсминца потребовали немедленной высадки их с корабля на берег. Сошли в Одессе и улетели домой в США, а эсминец с неполным экипажем ушёл к румынским берегам. В Интернете причину объяснили так: приближение российского самолёта вывело из строя все электронные системы корабля.
Известно, что световые фотоны излучаются и поглощаются электронами атомов. Оказалось, что масса фотонов середины светового диапаз
Дата добавления: 2016-06-22; просмотров: 4605;











