Теория формирования структуры фотона

Поскольку единичный фотон представляет собй частицу - корпускулу, которая движется прямолинейно и равномерно с большй скоростью , то это возможно при наличии в его структуре, так называемого вечного двигателя, который работает без внешней энергии. Это противоречило закону сохранения энергии, ошибочность которого мы уже доказали теоретически и экспериментально. Познакомимся с этим доказательством в главе «Научные проблемы энергоэффективности»

В качестве первого приближения к структуре фотона мы использовали кольцо (рис. 12) в виде окружности (рис. 13, а). Линейная частота 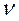в константе Планка 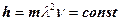вынуждает нас перейти к более сложной - шестигранной структуре фотона (рис. 13, b).

При вращении и прямолинейном движении такой структуры может формироваться траектория движения её центра масс, близкая по форме к синусоиде, которая описывается линейной частотой .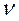

Принято считать, что если синусоидальная волна распространяется вдоль оси ОХ, то её положительная (+А) и отрицательная (-А) амплитуды равны, а ось ОХ является осью симметрии синусоиды (рис. 17, а).

При качении шестигранника (рис. 13, bи рис.17, b) его геометрический центр 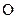является центром масс шестиугольника и описывает криволинейную траекторию (рис. 17, а). Какую?

Когда шестигранник в покое (рис. 17, b), то его центр О находится в нижнем положении, а когда он становится на ребро (рис. 17, с), то оказывается в самом верхнем положении. Расстояние от нижнего до верхнего положения центра шестигранника равно двум амплитудам 2А колебаний его центра масс относительно оси 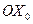(рис. 17, b и с), которая является осью симметрии этих колебаний. Из рис. 17. с находим связь амплитуды колебаний А центра шестиугольника с его радиусом 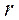. Она имеет вид

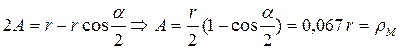. (43)

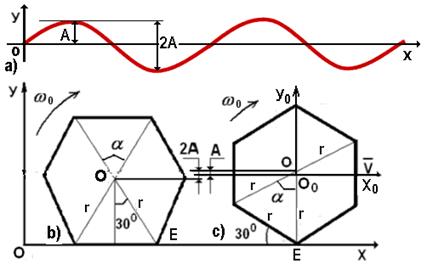
Рис. 17. а) синусоида; b) исходное положение геометрического центра О (центра масс) шестигранника; c) изменение положения центра масс О шестигранника при его повороте на угол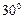

Обратим внимание на небольшую величину амплитуды 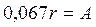(43) колебаний центра масс О шестигранника (рис. 17, b и с) в долях его радиуса и на то, что центр масс шестигранника совпадает с его геометрическим центром 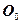(рис. 17, b и с), а у фотона (рис. 16) центр масс М не совпадает с его геометрическим центром 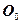(рис. 18). Из этого следует, что центр масс М фотона (рис. 16) описывает траекторию относительно его геометрического центра 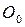- центра подвижной системы отсчёта 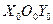(рис. 18, a).

Известно, что точка, зафиксированная на радиусе равномерно и прямолинейно катящейся окружности (рис. 12), может описывать различные траектории относительно неподвижной системы отсчёта . Траектория точки К (рис. 12 и рис. 18, а) называется обыкновенной циклоидой (рис, 18, b), траектория точки N (рис. 18, а) – удлинённой циклоидой (рис. 18, b), а траектория точки М (рис. 18, а) - укороченной циклоидой (рис. 18, b).

Совместим ось ОХ неподвижной системы отсчёта УОХ с осью 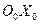подвижной системы отсчёта (рис. 18, a) и направим их так, чтобы они делили удвоенную амплитуду 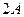укороченной циклоиды 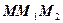(рис. 18, а) пополам, а вертикальную ось 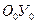оставим связанной с геометрическим центром 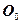фотона (рис. 16 и 18, а). Тогда его центр масс 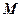не будет совпадать в движении с его геометрическм центром 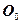(рис. 15 и 16 и 18, а) и будет описывать укороченную циклоиду 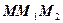(рис. 18, а и b).

Траектория соответствует повороту окружности радиуса 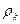на угол 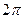с угловой скоростью 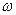(рис. 18, a).

Рис. 18: а) траектория 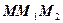- траектория движения центра масс 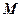фотона; b) траектории движения точек 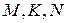: К – обыкновенная циклоида; N – удлинённая циклоида; М – укороченная циклоида

Совмещение вращательного и поступательного движений шестигранника (рис. 17, b) формируют движение его геометрического центра 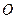,а значит ицента масс 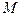фотона по укороченной циклоиде М (рис. 18, а).

Если время поворота шестигранника и фотона на угол и время поворота условной окружности радиуса 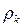(рис. 18, а и b) на угол 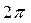будет одно и то же, то период колебаний геометрического центра 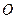шестигранника (рис. 17, b и с), а значит и центра масс М фотона (рис. 16), запишется так (рис. 18, а).

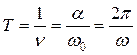, (44)

где 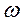- угловая скорость вращения условной окружности радиуса 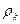(рис. 18, a). Из этих зависимостей имеем:

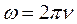, (45)

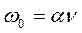. (46)

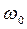Они показывают связь между угловыми скоростями и вращения условных окружностей с радиусам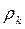и и 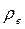и линейной частотой 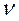колебаний геометрического центра 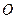(рис. 17, а и с) шестигранника, а значит и его центра масс.

На рис. 18, a хорошо видна траектория движения центра масс М фотона в интервале длины одной волны (рис. 18, a). Окружность радиуса 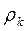делает за это время один полный оборот.

Обращаем внимание на то, что угловая скорость 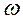условной окружности с радиусом 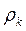, как это следует из зависимостей (44), связана с угловой скоростью 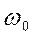условной окружности с радиусом 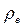простой формулой

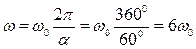. (47)

Скорость центра масс Е одного поля фотона (рис. 13, с) относительно подвижной системы отсчёт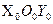а равна 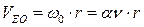. Если градусы угла 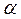перевести в радианы, то окружная скорость центров масс Е магнитных полей фотона (рис. 13, с) превышает поступательную скорость центра масс М фотона (рис. 15 и 16) на мизерную величину

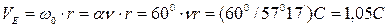. (48)

Итак, константа Планка в первозданном виде (33) может описывать лишь синусоидальный процесс и не имеет прямого отношения к вращательному процессу. Тем не менее, как мы уже показали, физический смысл момента импульса присутствует в формуле (33) косвенно и нам надо увидеть его явное проявление. Это возможно лишь при условии аналитического вывода основных соотношений (28-39) давно описавших движение фотона. Представляем аналитические выводы таких соотношений.

Для этого мы должны проследить за волновым движением центра масс 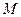всего фотона (рис. 16) и центров масс 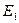отдельных его магнитных полей (рис. 13, с и рис. 16).

На рис. 19 показана схема перемещения центра масс 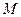фотона и центра масс 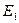одного его магнитного поля в интервале длины 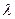одной волны.

Движение центра масс 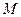фотона моделирует точка 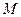, расположенная на расстоянии 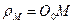от геометрического центра 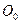фотона (рис. 18, а и 19). Движение центра масс одного магнитного поля фотона моделирует точка 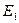, расположенная на расстоянии от его центра масс, равном 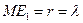(рис. 19).

Некоторые исследователи отмечали, что фотон имеет скрытые параметры. Если бы удалось найти их, то корпускулярные математические соотношения (28-39), описывающие его поведение, вывелись быаналитически. Попытаемся установить эти параметры.

Конечно, сложность модели фотона (рис. 16) затрудняет реализацию описанного плана. Однако если учесть, что фотон имеет плоскость поляризации, то движение его центра масс 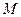в этой плоскости и движение центров масс 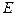шести его магнитных полей можно сопровождать качением условных окружностей, кинематические и энергетические параметры которых будут эквивалентны соответствующим параметрам фотона.

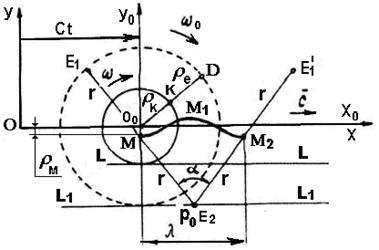
Рис. 19. Схема движения центра масс М фотона

и центра масс 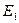одного его магнитного поля

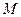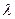Центр масс фотона совершает полное колебание в интервале длины его волны (рис. 17, c, 18, а и рис. 19), поэтому радиус условной окружности ради (первый скрытый параметр) описывает движение этого центра в интервале длины 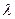одной волны. Он определится по формуле (рис. 19)

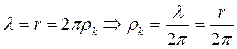. (49)

Кинематическим эквивалентом группового движения центров масс шести магнитных полей фотона будет вторая условная окружность. Её радиус 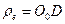(второй скрытый параметр) определяется из условия поворота центра масс каждого магнитного поля 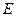фотона на угол 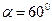в интервале каждой длины 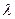его волны (рис. 18, а и рис. 19).

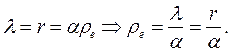(50)

Особо отметим, что время, в течение которого эти две условные окружностиповорачиваются на разные углы 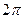и 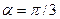, одно и то же, что соответствует Аксиоме Единства.

Кинематическая эквивалентность между движением сложной магнитной структуры фотона (рис. 15 и 16) и движением условных окружностей с радиусам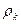и и 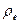позволяет вывести постулированные раннее математические соотношения, описывающие его поведение.

Сейчас мы увидим, как скрытые, ненаблюдаемые параметры фотона участвуют лишь в промежуточных математических преобразованиях и исчезают в конечных формулах.

Мы уже обозначили (рис. 19) угловую скорость условной окружности, описывающей движение центра масс 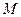фотона относительно его геометрического центра 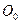символом 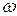(это - третий скрытый параметр), а угловую скорость условной окружности, описывающей движение центра масс каждого магнитного поля 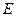, - через 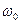(четвертый скрытый параметр), и линейную частоту - через 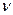, поэтому период колебаний центра масс 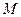фотона определится по формулам (44).

Соотношение связи между длиной волны 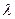, которую описывает центр масс 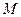фотона, и радиусом 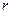имеет простой вид (рис. 17 и 19)

. (51)

Поскольку малая условная окружность радиуса 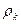перемещается в плоскости вращения фотона (рис. 19) без скольжения, то скорость любой её точки будет равна скорости её центра 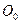и групповой скорости фотона. Используя соотношения (45) и (49), получим

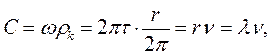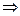(52 34)

что соответствует соотношению (34).

Аналогичный результат дают и соотношения (46) и (50) второй условной окружности радиуса .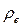

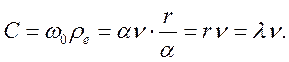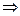(53 34)

Теперь видно, что вывод соотношений (34) и (52, 53) не только согласуется с моделью фотона (рис. 15 и 16) и механикой её движения (рис. 17, c, рис. 18, а и рис. 19), но и объясняет корпускулярные и волновые свойства фотона.

При выводе соотношения (29) обратим внимание на то, что кинетическая энергия движения фотона с массой 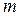эквивалентна кинетической энергии качения условной окружности с радиусом 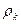с той же массой 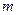, равномерно распределенной по её длине. Общая кинетическая энергия условной окружности c радиусом 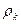будет равна сумме кинетической энергии её поступательного движения и энергии вращения относительно геометрического центра 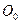. Используя зависимость (45) и (49), имеем

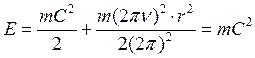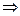. (54 29)

Тот же самый результат получится и при использовании второй условной окружности радиуса 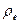(46) и (50).

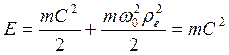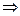. (55 29)

Приведем уравнение (54) к виду (32)

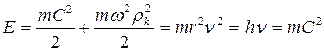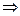, (56 32)

здесь .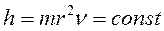

Вот теперь у нас есть полное право утверждать, что постоянством константы (36) Планка управляет закон сохранения момента импульса, который формулируется так: если сумма моментов внешних сил, действующих на вращающееся тело, равна нулю, то его момент импульса остаётся постоянным по величине и направлению, то есть постоянная Планка величина векторная .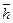

Механика движения фотона (рис. 18, a и табл. 3) ярко демонстрирует действие момента импульса на фотон при повороте его на каждые 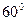. За один оборот фотона совершается 6 моментных импульсов. С учетом соотношений (44) получаем

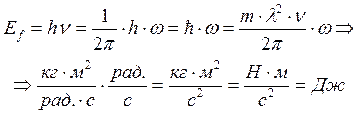. (57)

Таким образом, мы вернули истинный физический смысл размерности константы Планка - момент импульса. Линейная частота 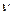имеет четкую связь с угловой частотой 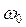вращения фотона (46).