Тороидальная модель электрона

Итак, электрон в первом приближении имеет форму кольца. В качестве второго приближения к электромагнитной модели электрона рассмотрим тор. Для начала будем считать его полым. Радиус окружности сечения тора (рис. 40) обозначим через .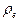

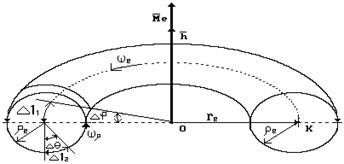
Рис. 40. Схема тороидальной модели электрона

Тогда площадь его поверхности определится по формуле

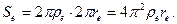(139)

Обозначим поверхностную плотность электромагнитной субстанции электрона 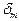. Тогда

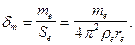(140)

Определим момент инерции полого тора. Из рис. 40 имеем

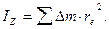(141)

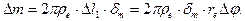(142)

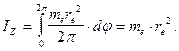(143)

Интересно то, что момент инерции полого тора равен моменту инерции кольца. Поскольку электрон проявляет одновременно электрические и магнитные свойства и имеет кинетический момент 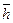, то у нас есть основания предполагать, что он имеет два вращения. Обычное вращение относительно оси симметрии с угловой частотой 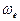назовем кинетическим вращением, формирующим его кинетический момент 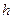и кинетическую энергию 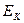. И второе - вихревое вращение относительно кольцевой оси с угловой частотой 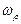(рис. 40, 41).

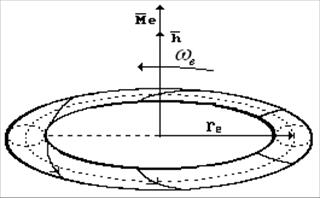
Рис. 41. Модель электрона с двумя вращениями: относительно центральной оси и относительно кольцевой оси тора

Назовем его потенциальным вращением, формирующим его потенциальную 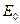энергию и магнитный момент 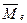. Вихревое вращение относительно кольцевой оси тора формирует магнитное поле электрона, поэтому потенциальная энергия электрона характеризует его потенциальные электрические и магнитные свойства.

При анализе энергетики электрона, как вращающегося кольца, мы показали, что его полная фотонная энергия 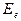состоит из равных между собой кинетической 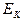и потенциальной 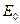составляющих. Посмотрим на возможность реализации этого постулата в тороидальной модели электрона. Кинетическая энергия вращения полого тора определится по формуле (рис. 41).

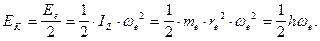(144)

Учитывая частоту 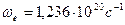(120), имеем

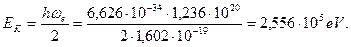(148)

Как видно (148), кинетическая энергия 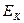электрона равна половине его полной, фотонной энергии (119), подтверждая работоспособность нашего постулата.

Величина радиуса 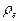окружности сечения тора (рис. 40) определяется из потенциального вращения электрона с частотой 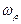. Для этого предполагаем, что

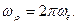(146)

Наступает очень важный момент. Нам трудно представлять линейную скорость какой-либо части электрона равной скорости света. Слишком она большая. Поэтому есть основания предполагать, что в этом случае математический символ скорости света С надо заменять равной ему совокупностью символов 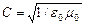. Тогда участие в формировании структуры электрона электрической 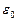и магнитной 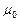постоянных усиливает физическую суть этого процесса, так как электрическая 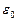и магнитная 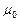постоянные – главные характеристики эфира.

Мы пока не будем делать такой замены, но отметим необходимость анализа каждого случая, где эта замена целесообразна.

Поскольку скорость света относительно пространства постоянна, то есть основания полагать, что скорость точек осевого кольца тора электрона в кинетическом вращении равна скорости точек поверхности тора в потенциальном вращении.

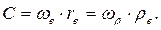(147)

Из этих соотношений найдем

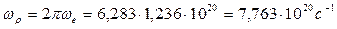(148)

и

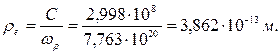(149)

Полагая, что вихревое вращение электрона генерирует его потенциальную энергию, имеем

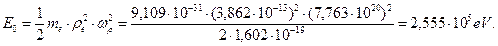(150)

Складывая результаты (145 и 150), получим полную фотонную энергию свободного электрона (119).

Итак, равенство кинетической и потенциальной энергий электрона даёт основание считать доказанными постулаты (145), (150). Удельная плотность массы полого тора электрона равна

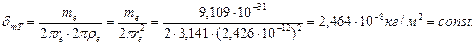(151)

Если мы на правильном пути, то из тороидальной модели электрона должна следовать математическая модель для расчета магнетона Бора 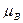. Учитывая радиус сечения тора 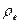(149) и известные зависимости между током 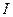и радиусом сечением провода 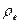( 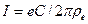), а также зависимость магнитного момента 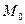формируемого током вокруг проводника ( 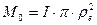) и пологая, что 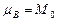, найдём магнетон Бора

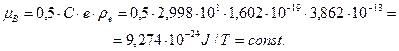(152)

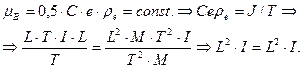(153)

Размерность (153) соблюдается, поэтому формула (152) заслуживает доверия. Совпадение результатов расчёта фотонной энергии электрона, магнетона Бора и радиуса электрона по разным формулам, даёт основание предполагать, что электрон представляет собой замкнутый кольцевой вихрь, формирующий тороидальную структуру, которая вращается относительно своей оси симметрии и относительно кольцевой оси тора, генерируя таким образом его кинетическую 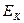и потенциальную 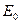энергии, а также магнитный момент электрона 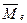равный магнетону Бора 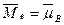(рис. 42, а).

Если показать всю совокупность линий, характеризующих магнитное поле электрона, то его модель примет форму, близкую к форме яблока (рис. 42, а).

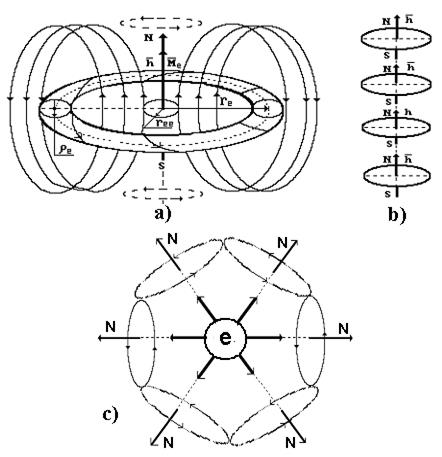
Рис. 42. а) схема теоретической модели электрона

(показана лишь часть магнитных силовых линий);

b) кластер электронов;

c) схема процесса излучения фотона электроном

Новая информация об электроне даёт основания считать, что, приводимая в справочниках величина 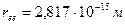, названная классическим радиусом электрона, является радиусом цилиндра, ограничивающего сближение магнитных силовых линий электрона, идущих вдоль оси его вращения в одном направлении (рис. 42, а - вверх). Достоверность этого подтверждает безразмерная величина тонкой структуры 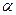, которая равна отношению длины окружности 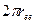указанного цилиндра к радиусу электрона .

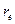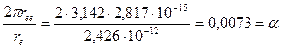. (154)

А теперь представим, что внешние силы начинают вращать такой тор в обратную сторону или тормозить его вращение (рис. 41). Сразу же на экваториальной поверхности тора образуется шесть вихревых, радиально направленных кольцевых полей (рис. 42, с).

Удаляясь от электрона, они формируют структуру из шести замкнутых друг с другом кольцевых магнитных полей. Малейшее изменение плотности одного из этих полей или малейшая удалённость его от геометрического центра формирует нецентральные силы, которые начинают вращать такую структуру. Возникающая асимметрия между её полями формирует неустойчивое положение такой структуры, автоматически влекущее её в прямолинейное движение со скоростью света 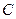(рис. 15 и 16).

Оставшаяся часть электрона (рис. 42, a) вновь восстанавливает свое вихрекольцевое движение, изменив соответственно угловые скорости 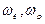и радиусы 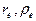так, чтобы отличие между ними в 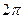раз сохранилось. Энергия электрона 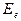уменьшится соответственно (119).

Так как энергия электрона равна произведению постоянной Планка на угловую частоту 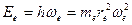, то после излучения фотона энергия электрона уменьшится за счет изменения его массы.

Чтобы постоянная Планка сохранила свое постоянство, радиус электрона 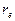должен увеличиться, а частоты 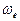- уменьшиться. Изменённые параметры электрона нарушают устойчивость его состояния, поэтому он вынужден восстановить исходную массу. Если вблизи есть фотон с такой массой, то он немедленно поглотит его и восстановит все свои константы. Если же вблизи нет фотона, необходимого для восстановления потерянной массы, то у электрона одна возможность – восстанавливать свою массу путем поглощения субстанции окружающей среды, которую мы называем эфиром. Он поглотит такое количество этой субстанции, которое восстановит его постоянную массу 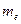. Автоматически восстановятся и все другие его параметры и 23 константы, управляющие его устойчивостью (рис. 43).

Рис. 43. Кадр из видео о формировании дельфином тора из воды

Таким образом, свободный электрон имеет строго постоянную массу 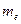, заряд 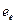и радиусы 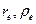. Когда он устанавливает связь с другим валентным электроном, то он тоже излучает фотон, и его параметры изменяются, но стабильность сохраняется благодаря энергии связи с другим валентным электроном. Если эту связь разорвать механическим путем, то исчезают условия пребывания электрона в стабильном состоянии. Чтобы восстановить эти условия, электрон должен поглотить излученный фотон или эквивалентное ему количество электромагнитной субстанции из окружающей среды, которую мы называем эфиром. Только после этого он сохранит свою устойчивость.

Обратим внимание на то, что радиусы световых и инфракрасных фотонов на много порядков больше радиуса электрона. Это значит, что в момент излучения удаляющиеся кольцевые магнитные поля формируют структуру фотона (рис. 42, с) на значительном расстоянии от электрона (рис. 41 и 42, а), определяемом длительностью переходного процесса от 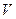до 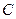. Это расстояние уменьшается с уменьшением радиуса излучаемого фотона. Поскольку радиус электрона равен радиусу рентгеновского фотона, то электрон не может излучить гамма-фотон. Эту функцию выполняет протон при синтезе ядер.

Таким образом, электрон имеет форму вращающегося полого тора (рис. 42, a). Его структура оказывается устойчивой благодаря наличию двух вращений. Первое - относительно оси, проходящей через геометрический центр тора перпендикулярно плоскости вращения, и второе - вихревое вращение относительно кольцевой оси, проходящей через центр окружности сечения тора (рис. 41).

Несколько методов расчета базового радиуса тора, включающих различные его энергетические и электромагнитные свойства, дают один и тот же результат, совпадающий с экспериментальным значением комптоновской длины волны электрона, а именно 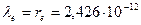м.

Итак, при обосновании модели электрона мы вовлекли в анализ уже существующие законы Кулона и Ньютона и следующие константы: константу локализации 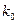, скорость света С, постоянную Планка 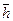, массу покоя электрона 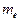, его заряд 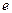, энергию покоя электрона, электрическую постоянную 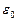, магнитную постоянную 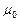, магнетон Бора 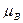, который мы обозначаем так 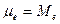, комптоновскую длину волны электрона, которую теперь надо называть комптоновским радиусом 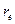электрона.

Другой важной характеристикой электрона является его спин. Он в точности равен постоянной Планка и является величиной векторной 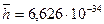. Её векторные свойства следуют из её размерности 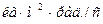- кинетического момента.

Третья важная характеристика электрона - магнитный момент 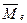или магнетон Бора, который генерирует напряженность 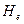магнитного поля электрона (рис. 42, а). В его геометрическом центре она равна 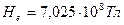. Это - значительная величина, но она интенсивно уменьшается по мере удаления от геометрического центра электрона вдоль оси его вращения.

Таким образом, электрон представляет собой полый тор, который имеет два вращения: относительно оси симметрии и относительно кольцевой оси тора (рис. 42, а). Вращением электрона относительно центральной оси управляет кинетический момент 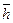- векторная величина. Вращение относительно кольцевой оси тора формирует магнитное поле электрона, а направления магнитных силовых линий этого поля формируют два магнитных полюса: северный N и южный S (рис. 42, а).

Модель электрона (рис. 42, а) невольно формирует представление о возможности образования кластеров электронов (рис. 42, b). Разноименные магнитные полюса могут сближать их, а одноименные электрические заряды ограничивать это сближение. В результате электроны, соединяясь друг с другом, могут формировать кластеры. Уже существует экспериментальное доказательство этому факту. Кроме этого уже установлено, что вся электростатика базируется на взаимодействии не положительных и отрицательных зарядов, а северных и южных магнитных полюсов кластеров электронов (рис. 42, b) в электростатических явлениях. Дальше мы познакомимся с этим подробнее.

Анализ изложенного показывает, что формированием структуры электрона (рис. 42, а) управляют 23 константы, в которых отразилась достоверность всех, сформулированных нами гипотез, и они приобрели статусы постулатов.

О модели протона

Информации о протоне меньше, чем об электроне, поэтому мы ограничимся первым приближением к его электромагнитной структуре. Как и следовало ожидать, в первом приближении модель протона, так же как и модели фотона и электрона, представляет собой кольцо.

Известно, что масса покоя протона 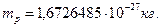Величина комптоновской длины волны протона равна

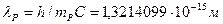. (155)

С учетом этого константа локализации протона оказывается равной константе локализации фотона и электрона

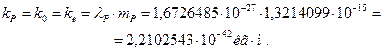(156)

Тогда, полагая, что протон, как и электрон, в первом приближении имеет форму кольца, получим

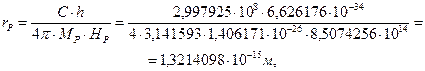(157)

где 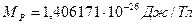- магнитный момент протона; 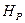- напряженность магнитного поля протона в его геометрическом центре, определяемая по формуле

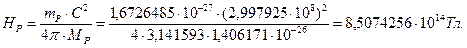(158)

Полученная величина радиуса протона (160) равна его комптоновской длине волны .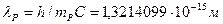

Вполне естественно предположить, что протон, также как и электрон, имеет классический радиус 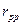. Его величина равна

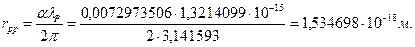(159)

Этот радиус 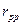на три порядка меньше радиуса 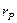(157), поэтому у нас есть основания считать, что это - радиус окружности в центре симметрии протона, ограничивающий сближение его магнитных силовых линий вдоль оси вращения (рис. 44).

Таким образом, базовый радиус протона (157) на три порядка меньше базового радиуса электрона (137). Спин протона также, как и электрона, равен постоянной Планка и направлен вдоль оси его вращения (рис. 44).

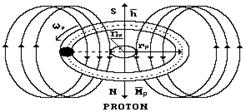
Рис. 44. Модель протона – сплошной тор

Знак заряда протона противоположен знаку заряда электрона. Это требует противоположного направления векторов спина 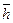и магнитного момента 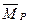(рис. 44). Формула (118 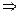160), связывающая постоянную Планка и магнетон Бора, отражает это требование.

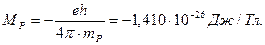(160)

Дальше, при анализе процесса формирования молекул мы получим подтверждение того, что векторы спина и магнитного момента у электрона совпадают по направлению, а у протона - противоположны. Поэтому формулу (118 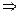160) надо писать с плюсом для электрона (рис. 42, а) и с минусом для протона (рис. 44).

Напряженность магнитного поля протона вблизи геометрического центра его кольцевой модели (162) столь велика, что у нас появляются основания считать, что такая напряженность способна формировать магнитные силы, соединяющие протоны и нейтроны ядра атома, которые называются ядерными силами.

Напряженность магнитного поля вблизи геометрического центра протона можно также рассчитать и по другой формуле, используя его фотонную энергию

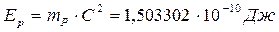. (161)

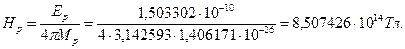(162)

Как видно, она совпадает с величиной, определённой по формуле (158). Если магнитное поле протона подобно магнитному полю стержневого магнита, то разноименные магнитные полюса таких полей будут сближать протоны, а их одноименные электрические заряды – ограничивать это сближение. Дальше мы увидим, что такое явление наблюдается при образовании молекулы водорода, а также при выполнении атомом водорода функции соединительного звена при формировании различных молекул.

Если протон имеет форму тора, заполненного эфирной субстанцией, то объёмная плотность 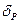этой субстанции должна быть близка к плотности ядер атомов .

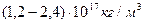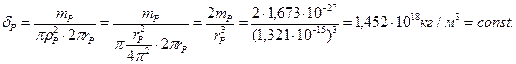(163)

Как видно (163), это действительно так. Плотность протона больше плотности ядер, так как ядро - это не плотная компоновка протонов и нейтронов.

Если представить протон в виде сферы с радиусом 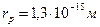(рис. 44), то при непосредственном контакте двух протонов между ними будет действовать кулоновская сила отталкивания

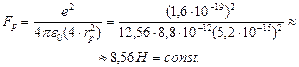(164)

Для сравнения вычислим силу гравитации, действующую в этом случае между протонами.

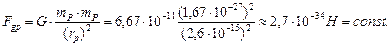(165)

Результаты этих расчетов убедительно доказывают, что при формировании ядер атомов решающую роль играют не силы гравитации, а магнитные силы. Они и формируют ядра атомов.

Чтобы сформировалось более или менее четкое представление о модели протона, отметим, что в первом приближении это кольцо, а во втором – сплошной тор. С учетом совокупности магнитных силовых линий протон можно представить в виде геометрической фигуры, имеющей форму яблока с магнитными силовыми линиями, проходящими вдоль оси яблока и замыкающимися друг на друга. Такая модель имеет два магнитных полюса: северный и южный. Полюса формируются на разных концах оси вращения кольца. При этом направления векторов 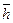и 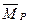противоположны. Это и даёт нам основание постулировать тороидальную модель протона (рис. 44) с вихревым вращением, противоположным аналогичному вращению у тороидальной модели электрона (рис. 35, а). Но плотность сплошного тора, близкая к плотности ядер атомов, наводит на мысль, что тор протона имеет лишь одно вращение, которое и определяет его электрический заряд, поэтому мы представим модель протона пока в виде сплошного тора, осевая линия которого – базовое кольцо протона (рис. 44).

О модели нейтрона

Известно, что масса покоя нейтрона 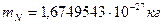. Нейтрон также имеет магнитное поле и магнитный момент 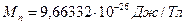. Величина комптоновской длины волны нейтрона равна 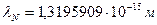. Константа локализации нейтрона оказывается равной константе локализации фотона, электрона и протона.

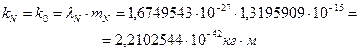. (166)

Нейтрон не имеет заряда. Поскольку масса нейтрона незначительно отличается от массы протона, то комптоновские значения их длин волн или радиусов имеют близкие значения (157), (167). Главное свойство постулированного нами магнитного поля нейтрона – шесть взаимно перпендикулярных магнитных полюсов: три северных и три южных (рис. 45).

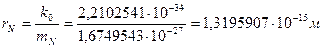(167)

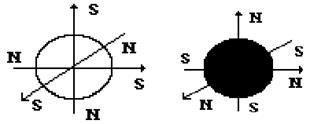
Рис. 45. Схема модели нейтрона

Дальше мы увидим, что такое свойство магнитного поля нейтрона автоматически выявляет структуры ядер атомов и - уже сфотографированных молекул и кластеров графена и бензола. Теоретическая величина радиуса нейтрона равна (167).

Таким образом, константы локализации основных элементарных частиц: фотона, электрона, протона и нейтрона равны одной и той же величине.

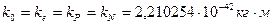. (168)

Известно, что разность между массой нейтрона и протона равна 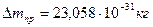. Масса нейтрона больше массы протона на 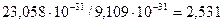масс электрона. Из этого следует, чтобы протон стал нейтроном, он должен захватить 2,531 электрона. Поскольку не существует электронов с дробной массой, то протон должен поглощать целое число электронов. Если он поглотит три электрона, а его масса увеличится только на 2,531 масс электрона, то возникает вопрос: куда денется остаток массы электрона 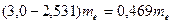? Ортодоксальная физика нарушенный баланс масс в этом процессе объясняет просто: рождением нейтрино, которое не имеет заряда, поэтому, как считается в ортодоксальной физике, рождение этой частицы очень сложно зарегистрировать. Однако, дальше мы увидим, что превращение не поглощенной части электрона протоном в эфир – более плодотворная гипотеза.

Если иметь в виду классический радиус нейтрона, аналогичный классическому радиусу электрона и протона, то он будет равен

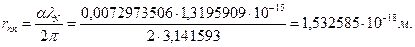(169)

Мы не видим оснований приписывать этот радиус геометрическому размеру всего нейтрона. Скорее всего, это - размер какой-то его части, которую мы назвали радиусом сечения полости центрального магнитного поля, ограничивающим сближение его магнитных силовых линий.

Заключение

Существующие и дополнительные математические модели рассчитывают основные параметры электрона, протона и нейтрона, полученные экспериментально. Сходимость теоретических и экспериментальных результатов настолько значительна, что у нас есть основания использовать полученные модели электрона, протона и нейтрона для интерпретации экспериментов и дальнейших теоретических и экспериментальных исследований.