Кольцевая модель электрона

Известно, что электрон имеет собственную энергию, которую обычно определяют по формуле 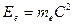. Однако смысл такого допущения не всегда расшифровывается. А он заключается в том, что если всю массу электрона перевести в массу фотона, то энергия электрона будет равна 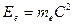. Этот факт имеет экспериментальное подтверждение. Известно, что массы электрона и позитрона равны. Взаимодействуя друг с другом, они образуют два фотона. Вот почему мы можем приписать электрону энергию, равную энергии фотона, имеющего соответствующую массу. Энергию электрона 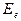, равную энергии фотона, назовем фотонной энергией электрона. А теперь исследуем возможности кольцевой модели (рис. 37, а) свободного электрона.

Для этого предполагаем, что электрон имеет равные между собой кинетическую 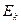и потенциальную 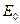энергии, сумма которых равна его фотонной энергии .

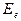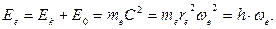(118)

Расчет по этой формуле дает такое значение фотонной энергии электрона

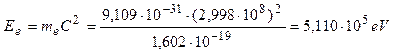. (119)

Если свободный электрон вращается только относительно своей оси, то угловая частота 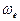вращения кольцевой модели свободного электрона, определенная из формулы (118), оказывается равной

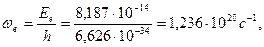(120)

а радиус кольца электрона равен его экспериментальной величине (107) и (109)

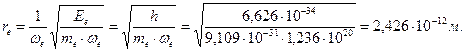(121)

Как видно, теоретические величины угловой скорости электрона, определённые по разным формулам (116) и (120), равны. Теоретические величины радиуса кольца электрона, определённые по формулам (107) и (121), равны экспериментальному значению комптоновской длины волны электрона 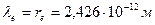(109).

Таким образом, не выявив пока структуру электрона, мы получили его упрощенную модель – кольцо (рис. 37, а). Эта модель помогает нам анализировать механическое поведение электрона, но почти не содержит информации о его электромагнитных свойствах. Поэтому поищем такие математические модели, описывающие поведение кольцевой модели электрона, которые содержали бы его заряд 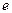, магнитный момент 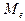и напряженность магнитного поля .

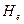При поиске этих математических моделей не обойтись без новых гипотез. Основания для их формулировки возьмём из теоретической и экспериментальной информации, описывающей поведение заряженных элементарных частиц в магнитных полях (рис. 38, а).

Эксперименты на ускорителях элементарных частиц показали, что криволинейная траектория электрона в магнитном поле хорошо описывается математической моделью, отражающей равенство между центробежной силой инерции, действующей на электрон, и силой магнитного поля.

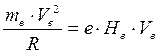. (122)

Тут невольно возникает предположение, что процессом формирования кольцевой структуры электрона управляет этот же закон. Рассмотрим плодотворность этой гипотезы. Поскольку электрон, как мы предполагаем, имеет форму кольца, то для описания процесса формирования кольца надо перевести соотношение (122) в дифференциальную форму. Полагаем, что заряд электрона равномерно распределен по длине его кольцевой модели и каждый элемент кольца 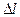имеет массу 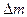и заряд 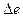(рис. 38, b).

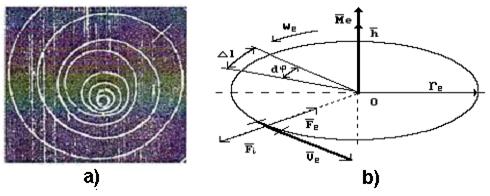
Рис. 38. Схема кольцевой модели электрона

На каждый элемент кольца будет действовать несколько сил: сила инерции 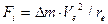, кулоновские силы расталкивания, силы магнитного взаимодействия и какие-то другие, пока неизвестные нам силы. Мы будем предполагать, что центростремительная сила, т.е. результирующая сила, искривляющая траекторию отдельных элементов кольца и заставляющая кольцо совершать вращательное движение вокруг оси, будет равна 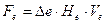(рис. 38, b и формула 122). Дальнейший анализ, как будет показано, подтвердит плодотворность этого предположения и оно превращается в постулат.

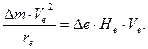(123)

Проверим размерности правой и левой частей формулы (123).

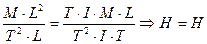. (124)

Они одинаковы, значит формулы (122 и 123) заслуживают доверия. Обозначая массовую плотность кольца 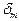, а зарядовую - 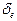, имеем:

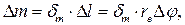(125)

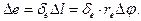(126)

Поскольку

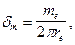(127)

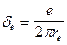(128)

и 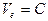, то уравнение (123) принимает вид

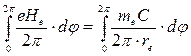. (129)

Интегрируя, найдём

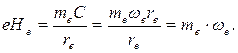(130)

Итак, мы получили математическое соотношение, в которое входят: масса 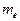свободного электрона, его заряд 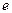, напряженность магнитного поля 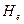внутри кольца, которая генерируется зарядом вращающегося кольца, угловая частота 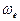и радиус 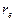кольца электрона. Недостает в этом соотношении магнетона Бора .

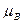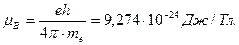(131)

Обратим внимание на тот факт, что в приведенной формуле (131) 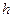- величина векторная, она придает векторные свойства и магнетону Бора .

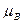Преобразуем соотношение (130) следующим образом

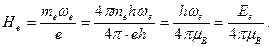(132)

Из этого имеем

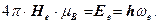. (133)

Теперь мы можем определить из соотношения (132) напряженность 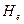магнитного поля внутри кольцевой модели электрона, угловую скорость 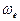вращения кольца и его радиус .

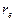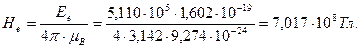(134)

Обратим внимание на очень большую напряженность (134) магнитного поля в центре симметрии электрона. Из (132) имеем

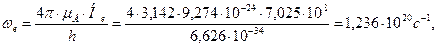(135)

что полностью совпадает со значениями этой величины, определенными по формулам (116) и (120).

Из формулы (134) следует ещё одна математическая модель для расчета радиуса электрона

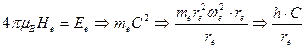. (136)

Отсюда

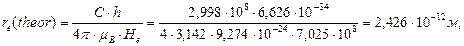(137)

где 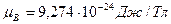- магнетон Бора; 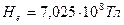- напряженность магнитного поля в центре симметрии электрона.

Итак, главный параметр кольцевой модели свободного электрона - радиус кольца 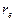, определённый по формулам (107), (121) и (137), оказался одинаковым и равным экспериментальной величине длины волны электрона (109).

Недостаток кольцевой модели электрона в том, что она не раскрывает причину рождения позитрона, поэтому кольцо должно иметь какую-то внутреннюю структуру. Поиск этой структуры - следующая задача. Прежде чем приступить к ее решению, обратим внимание на схему кольцевой модели электрона, следующую из наших расчетов (рис. 37, а). Самой главной особенностью теории и модели электрона является совпадение направлений векторов 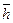и 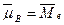.Назовем символ 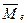магнитным моментом электрона.

Теория фотона убедительно показывает, что формированием структур фотонов всех диапазонов управляет закон сохранения момента импульса 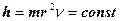. Он - следствие жизни фотонов в движении со скоростью света.

Так как электрон и другие элементарные частицы могут находиться в покое в свободном состоянии, то закон сохранения момента импульса уже не может управлять формированием их структур и ихвзаимодействиями.

Формированием структур элементарных частиц, которые могут быть в относительном покое при свободном состоянии, управляет закон сохранения кинетического момента

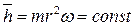. (138)

Чтобы понять физическую суть работы закона сохранения кинетического момента (138) проанализируем вращение фигуриста (рис. 39, а и b) относительно оси, проходящей вдоль его тела. Посмотрите, как выражается этот закон математически для тела, совершающего только вращательное движение, .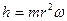

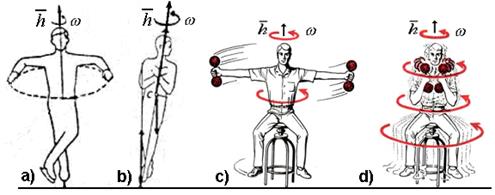
Рис. 39. Наглядная работа закона сохранения кинетического момента

Вы сразу узнали константу Планка. В эту константу Природа и заложила этот закон. Он работает в условиях отсутствия внешнего воздействия на вращающееся тело. Если рассматривать вращение фигуриста, то он, конечно, испытывает внешнее воздействие. Оно проявляется в виде сопротивления, создаваемого воздухом, а также в виде сил трения, действующих на коньки фигуриста. Так что закон этот проявляется здесь не в чистом виде. Но, тем не менее, небольшое сопротивление воздуха и льда дают нам возможность увидеть проявление этого закона.

Посмотрите на выражение константы Планка ещё раз 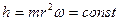. Масса 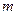фигуриста в момент его вращения не изменяется. Однако распределение этой массы изменяется. Когда он разводит руки (рис. 39, а), то они удаляются от оси его вращения и момент инерции 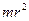фигуриста увеличивается, так как величина, равная массе рук, умноженной на квадрат расстояний 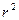их центров масс от оси вращения, растет.

Сразу видно, чтобы константа Планка 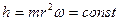осталась постоянной, скорость вращения 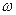фигуриста должна уменьшиться (рис. 39, а). Когда же он (или она) приближает руки к оси своего вращения, то видно (рис. 39, b) что произойдет со скоростью вращения 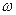при .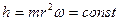

Когда фигурист приближает руки к оси своего вращения, то величина 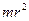уменьшится, так как уменьшится расстояние 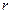для центров масс рук. Чтобы величина 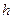осталась постоянной, скорость 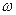вращения фигуриста должна возрасти. Что мы и наблюдаем (рис. 39, b).

Конечно, если бы не было никакого сопротивления, то фигурист мог бы вращаться вечно, как и фотон в движении живёт миллиарды световых лет, принося нам информацию от звёзд далёких галактик.

Наиболее наглядно проявление закона сохранения кинетического моментанаблюдается и при вращении человека, сидящего на вращающемся стуле и разводящем в стороны (рис. 39, с) или прижимающем к груди (рис. 39, d) руки с гантелями.

Обратим внимание ещё раз на размерность константы Планка (115). В классической механике эта размерность соответствует векторной величине и называется кинетический момент. Так как он постоянен, то его постоянством управляет закон сохранения кинетического момента.

Таким образом, основные элементарные частицы можно представлять в первом приближении в виде вращающихся колец (рис. 37, а). Вектор 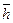направлен вдоль оси вращения кольца так, что если смотреть с его острия, то вращение будет направлено против хода часовой стрелки. Константу Планка 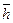в этом случае называют спином (рис. 37, а и b).