Теорема Поклингтона.

Пусть n=RF+1, F= 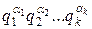- каноническое разложение.

Если 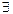a: 1) a^n—1≡1(mod n);

2) 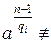1(mod n) .

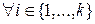p≡1(mod F) для любого простого p\n.

■

Итак, если разложить n—1 на два сомножителя n—1=RF, где F> 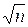—1, то, если для некоторого a будут выполнены условия Теоремы Поклингтона (1) и (2), то n – простое.

Таким образом, можно значительно сократить количество проверок по сравнению с тестом Миллера.

Замечание.

Если n=RF+1 – нечетное простое число, F> 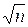—1, F= 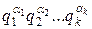, НОД(R,F)=1, то вероятность того, что случайно выбранное 1<a<n будет удовлетворять условиям (1), (2) теоремы Поклингтона, есть .

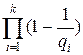Замечание.

Если известно полное разложение n—1, то в качестве F следует брать число, составленное из наибольших делителей n—1 для того, чтобы:

1) сократить число проверок условия (2) для каждого a;

2) уменьшить степени, в которые возводится a на этапе проверки (2);

3) повысить вероятность того, что случайно выбранное a будет удовлетворять условию (2), а значит уменьшить количество перебираемых a.

Пример.

n=4021. 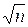—1<63.

n—1=4020=2²·3·5·67. F=67, R=2²·3·5=60.

Проверка условий:

a=2.

1) 2⁴⁰²⁰ mod 4021=1.

2)2⁶⁰—1 mod 4021=1451.

НОД(4021,1451)=1.

n=4021 – простое число.

(Заметим, что вероятность того, что наугад выбранное a будет удовлетворять условиям теоремы Поклингтона для данного примера, есть (1—1/67)≈0,985).