Интегральное исчисление решает обратную задачу – нахождение самой функции по ее производной или дифференциалу.
Определение 1: Функция F(x) называется первообразной функцией для функции f(x) на промежутке I, если в каждой точке x этого промежутка F 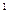 (x)=f(x).
(x)=f(x).
Пример: F(x) = 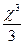 ; т.к .F
; т.к .F 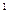 (x) = f(x) = x
(x) = f(x) = x 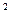 ;
;
F(x) = -сtg x т.к. F 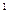 (x) = f(x) =
(x) = f(x) = 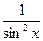
Но F 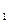 (x) =
(x) = 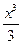 +5; F
+5; F 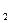 (x) =
(x) = 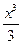 -2; F
-2; F 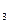 (x) =
(x) = 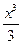 +25,094 таковы,
+25,094 таковы,
что F 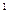
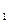 (x)=F
(x)=F 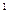
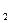 (x)=F
(x)=F 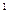
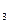 (x)= x
(x)= x 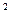 ,
,
т.е. для заданной функции существует множество первообразных, отличающихся друг от друга постоянным слагаемым.
Основное свойство первообразных:
Если F(x) – одна из первообразных функции f(x) на промежутке I, то все множество ее первообразных может быть записано в виде F(x)+C, где С – любое действительное число.
Определение 2:Совокупность всех первообразных для функции f(x) на промежутке I называется неопределенным интегралом от функции f(x) и обозначается 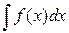 , где
, где 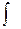 -знак интеграла; f(x) – подынтегральная функция; f(x)dx – подынтегральное выражение.
-знак интеграла; f(x) – подынтегральная функция; f(x)dx – подынтегральное выражение.
Таким образом, из определения неопределенного интеграла и основного свойства первообразной следует выполнение равенства
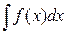 = F(x)+C (*), = F(x)+C (*),
|
где F(x) – некоторая первообразная для f(x), С – произвольная постоянная.
Примеры: 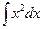 =
= 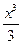 +С, т.к.
+С, т.к. 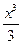 - первообразная для
- первообразная для 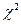
.
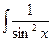
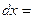 - ctgx +C, т.к. -ctgx – первообразная
- ctgx +C, т.к. -ctgx – первообразная
для 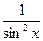 .
.
Дата добавления: 2020-07-18; просмотров: 762;











