Исследование корней по знаку дискриминанта
Рассмотрим неполное кубическое уравнение с действительными коэффициентами, то есть уравнение
y3+py+q=0, где p, qÎR. (1)
дискриминантом уравнения (1) будем называть выражение
D= 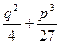 .
.
Так как p, qÎR, то, очевидно, DÎR, поэтому возможен лишь один из трех случаев: D>0, D=0, D<0.
Итак, пусть D>0Û 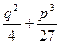 >0 Þ
>0 Þ 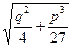 ÎRÞ
ÎRÞ 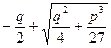 ÎR.
ÎR.
В теории функций действительных переменных доказывается, что существует хотя бы один действительный корень нечетной степени из действительного числа. следовательно, среди значений u1, u2, u3 обязательно есть хотя бы одно действительное, выберем его в качестве u1.
Таким образом, u1ÎRÞ v1= 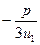 ÎR Þ y1=u1+v1ÎR,
ÎR Þ y1=u1+v1ÎR,
y2=- 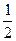 (u1+ v1)+i
(u1+ v1)+i 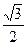 ( u1- v1) ÎC, так как u1¹ v1,
( u1- v1) ÎC, так как u1¹ v1,
y3=- 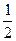 (u1+ v1)-i
(u1+ v1)-i 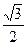 ( u1- v1) ÎC, так как u1¹ v1.
( u1- v1) ÎC, так как u1¹ v1.
Все сказанное позволяет сделать вывод:
Если дискриминант кубического уравнения с действительными коэффициентами положителен, то уравнение имеет один действительный и два комплексно сопряженных корня.
пусть D=0Û 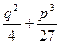 =0Û
=0Û 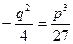 Þ
Þ 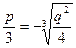 Þ u1-3=
Þ u1-3= 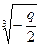 , где
, где 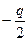 ÎR, следовательно, среди значений u1, u2, u3 обязательно есть хотя бы одно действительное, выберем его в качестве u1 =
ÎR, следовательно, среди значений u1, u2, u3 обязательно есть хотя бы одно действительное, выберем его в качестве u1 = 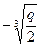 , тогда v1=
, тогда v1= 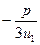 =
= 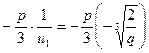 = -
= - 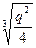
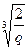 =
= 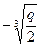 ÎR, y1=u1+v1=
ÎR, y1=u1+v1= 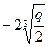 ÎR,
ÎR,
y2=- 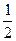 (u1+ v1)+i
(u1+ v1)+i 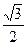 ( u1- v1)= -
( u1- v1)= - 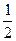 (
( 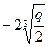 )=
)= 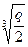 ÎR,
ÎR,
y3=- 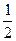 (u1+ v1)-i
(u1+ v1)-i 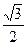 ( u1- v1)= -
( u1- v1)= - 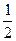 (
( 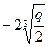 )=
)= 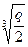 ÎR,
ÎR,
Cказанное позволяет сделать вывод:
Если дискриминант кубического уравнения с действительными коэффициентами равен нулю, тогда уравнение имеет три действительных корня, причем два из них равны между собой.
Наконец, пусть D<0Û 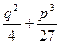 <0
<0
Замечание. Так как DÎR, то последнее неравенство возможно только при в том случае, если р<0.
Обозначим 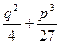 =-b2, где bÎR, b¹0, тогда
=-b2, где bÎR, b¹0, тогда
u1-3= 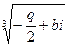 , v1-3=
, v1-3= 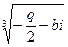
Для нахождения u1 , u2 , u3 найдем модуль и аргумент комплексного числа, записанного под знаком корня:
r= 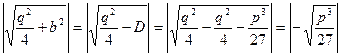 ,
,
cosj=- 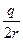 ,
,
sinj= 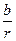 >0,
>0,
u1-3= 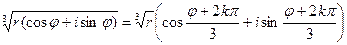 ,
,
k=0,
u1= 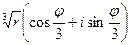 ,
,
k=1,
u2= 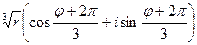 ,
,
k=2,
u3= 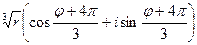 ,
,
v1-3= 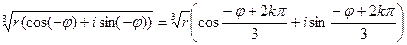 ,
,
k=0,
v1’= 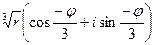 ,
,
k=1,
v2’= 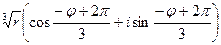 ,
,
k=2,
v3’ = 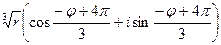 .
.
Теперь, пользуясь соотношением uv= 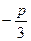 , подбираем пары соответствующих значений. Так как uvÎR, то arg(uv)=kπ, то есть argu+argv=kπ, kÎZ.
, подбираем пары соответствующих значений. Так как uvÎR, то arg(uv)=kπ, то есть argu+argv=kπ, kÎZ.
В качестве упражнения показать, что
y1=u1+v1’, y2=u2+v3’, y3=u3+v2’.
Таким образом,
y1= 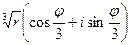 +
+ 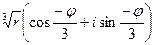 =
= 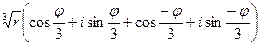 =
=
= 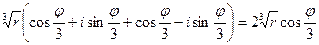 ÎR,
ÎR,
y2= 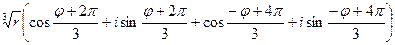 =
=
= 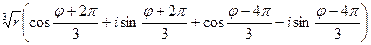 =
=
= 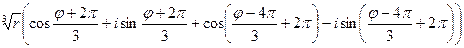 =
=
= 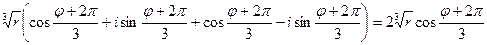 ÎR,
ÎR,
y3= 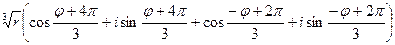 =
=
= 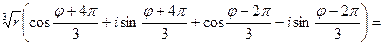
= 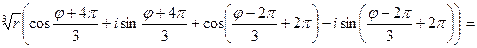
= 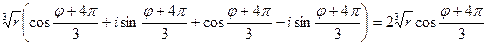 ÎR.
ÎR.
Вывод: Если дискриминант кубического уравнения с действительными коэффициентами отрицателен, тогда уравнение имеет три действительных различных корня.
Дата добавления: 2020-10-25; просмотров: 573;











