Построение регрессионной модели стохастического объекта

Пусть задан некоторый стохастический объект (рис. 2.6) входная и выходная координаты X и Y которого являются случайными величинами.

На Y влияет не только входная координата X, но и случайная помеха Z (нестабильность режима работы объекта, стохастические воздействия внешней среды, погрешности измерения Y и т.д.). Поэтому нельзя говорить о функциональной зависимости Y от X. В подобных случаях следует говорить о наличии стохастической (вероятносной) связи между переменными X и Y объекта в статике.

Случайные величины X и Y являются зависимыми, если закон распределения вероятностей одной из них зависит от значений другой, т. е.

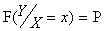{Y<y при условии X=x}

Функция 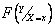, или просто 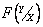, называется условным интегральным законом распределения вероятностей Y при X=x. 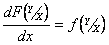называется условной плотностью распределения вероятностей.

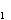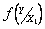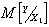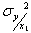Предположим, что можно установить X=x , тогда поведение случайной величины Y будет полностью характеризоваться условной плотностью распределения вероятностей . Обозначим условные числовые характеристики Y - математическое ожидание и дисперсию - через и . Затем зафиксируем X=x 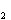и найдем 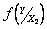, , 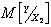, 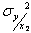положим X=x 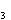, найдем 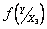, , , 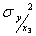и т.д.

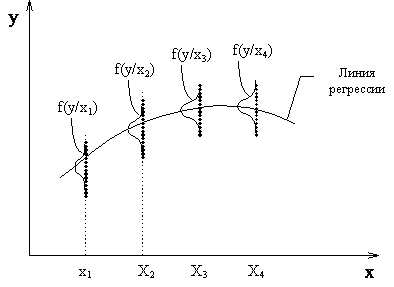
рис. 2.7

Будем считать, что структура 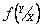не зависит от x, а параметры функции плотност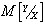и и 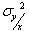зависят от того, какое значение x принимает случайная величина X.

Зависимость 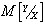от x называется регрессионной. Ниже будем говорить только о регрессионной зависимости

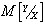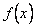= . (5.61)

Регрессионная зависимость показывает, как изменяется среднее значение Y при изменении X.

Если соединить плавной линией точки 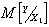, , 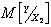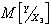и т.д., то получим линию регрессии. Эта линия есть статическая характеристика объекта.

Уравнением регрессии называют функцию 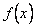, описывающую линию регрессии. Уравнения регрессии классифицируют на линейные (корреляционные) и нелинейные.

При построении регрессионной модели статики (5.61) объекта широко применяется пассивный метод идентификации. Этот метод применяют при изучении статики объектов, уровень помех которых достаточно велик, а также в тех случаях, когда недопустимо нанесение искусственных возмущений на входе объекта.

Пассивный метод идентификации основан в получении статистической информации об объекте по данным его нормальной эксплуатации. Затем реализации входной x и выходной y величин обрабатываются таким образом, чтобы определить регрессионную модель

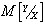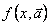= , (5.62)

где - вектор коэффициентов модели.

Определение уравнения регрессии состоит из двух этапов: выбор типа уравнения регрессии и расчет его коэффициентов.

Первый этап обычно осуществляется либо путем эмпирического подбора типа уравнения регрессии по виду корреляционного поля между входными и выходными величинами, либо путем теоретического изучения закономерности физического процесса, отражением которого является стохастическая связь между этими величинами. Иногда оба подхода используются в сочетании друг с другом.

Второй этап - расчет коэффициентов уравнения регрессии - чаще всего выполняется методом наименьших квадратов. При этом минимизация по 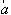выражения

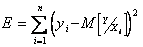(5.63)

приводит к оценкам вектора . Очевидно, на данной реализации для принятого уравнения модели объекта (5.62) полученные оценки дают наименьшее СКО реализации, полученной по модели от наблюдаемой реализации 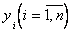объекта.

Следует отметить, что пассивно - статистический метод имеет целый ряд существенных недостатков по сравнению с активными методами:

1) полученная модель объекта справедлива только в пределах использованного экспериментального статистического материала;

2) трудно разделить эффекты от коррелированности части входных величин многомерного объекта;

3) индивидуальные коэффициенты регрессии не имеют какого-либо физического смысла;

4) не извлекается информация об ошибке опытов;

5) требуется получить большой объем экспериментальных данных и производить трудоемкие вычисления.

Указанные недостатки в значительной степени снижают ценность моделей, полученных пассивно-статистическим методом. К этому методу прибегают только в тех случаях, когда другие методы не могут быть использованы.

Предварительный анализ экспериментального статистического материала составляет основную задачу корреляционного анализа при идентификации стохастического объекта. При этом суть корреляционного анализа сводится к оценке силы стохастической связи между случайными величинами X и Y и установлению вида зависимости между ними в виде уравнения регрессии.

Чтобы предварительно определить наличие корреляционной связи между X и Y, наносят экспериментальные точки 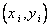на график и строят корреляционное поле (рис. 2.8).

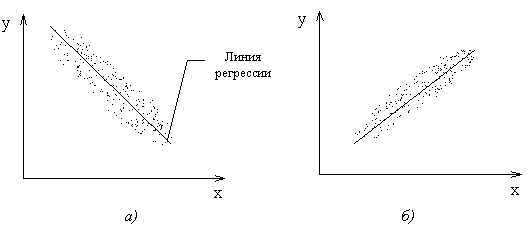
Рис. 2.8

На рис. 2.8 представлены:

а - сильная отрицательная корреляция;

б - сильная положительная корреляция;

в - слабая положительная корреляция;

г, д - отсутствие корреляции.

По тесноте группирования точек вокруг прямой или кривой линии, по наклону линии можно визуально судить о наличии корреляционной связи.

Корреляционное поле характеризует вид связи между X и Y, т.е. наличие линейной или нелинейной зависимости.

Существует три вида корреляции - линейная, нелинейная и множественная корреляция. При линейной корреляции линия регрессии аппроксимируется уравнением прямой, при нелинейной - уравнением кривой. Множественная корреляция определяет связь между многими величинами, и при этом используется уравнение множественной регрессии.

Наиболее распространенной является линейная корреляция.

Понятие корреляции дает возможность судить о том, насколько тесно ложатся экспериментальные точки на аппроксимирующую кривую линии регрессии. Если регрессия определяет предполагаемое соотношение между переменными, то корреляция показывает, насколько хорошо это соотношение отражает действительность.

Задача стохастического анализа объекта ставится таким образом: по данной выборке объема n оценить силу (тесноту) корреляционной связи между X и Y, найти уравнение приближенной регрессии и оценить допускаемую ошибку.

Оценка тесноты корреляционной связи. В общем виде задача выявления и оценки силы стохастической связи не решена. Существуют показатели, оценивающие те или иные стороны стохастической связи.

Поведение случайной величины Y описывается обычно следующими функциональными и числовыми характеристиками:

- интегральным законом распределения вероятностей ;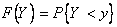

- дифференциальным законом распределения вероятностей 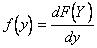( или плотностью вероятностей );

- математическим ожиданием ;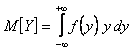

- дисперсией .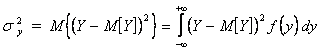

Отметим, что 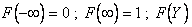— возрастающая функция. Если F(Y) непрерывна по Y, то 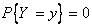, однако, 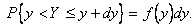Кроме того, .

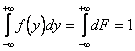Поведение системы двух случайных величин X,Y, значения x и y которых изменяются от 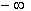до 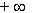, полностью описывается интегральным законом распределения вероятностей

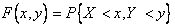
или плотностью распределения вероятностей

,

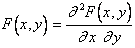т.е.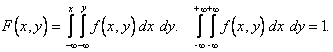

Отметим, что 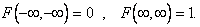Функция F(x,y) есть неубывающая функция x, y, т.к. с ростом x и y вероятность выполнения двух неравенств X < x, Y < y не может уменьшаться. Далее, 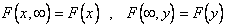, где F(x) и F(y) - функции распределения X и Y.

По известным f(x,y) всегда можно найти f(x) и f(y).

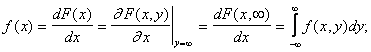
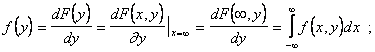
Обратная задача - определение f(x,y) по известным f(x) и f(y) в общем случае не имеет решения т.к. эти две функции не характеризуют взаимную зависимость величин X и Y. Но для независимых случайных величин f(x,y) = f(x)f(y).

Основной числовой характеристикой двух случайных величин X и Y является ковариационный (корреляционный) момент

.

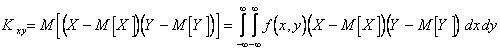Назовем случайную величину 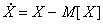центрированной, ее значение 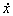есть отклонение x от среднего значения M[X]. Тогда

Момент 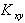равен среднему значению произведения двух центрированных случайных величин 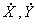и характеризует тесноту взаимной связи X и Y.

Действительно, пусть X и Y независимы, тогда f(x,y) = f(x)f(y) и

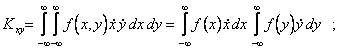
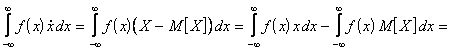
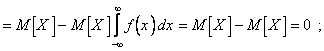
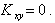
Обратное утверждение - если 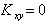, то X и Y независимы - в общем случае доказать нельзя. Более того, можно найти пример, в котором 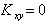, а X и Y - зависимые случайные величины.

Следовательно, величина 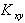не является исчерпывающей характеристикой силы связи X и Y. Оказывается, что 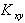характеризует только линейную зависимость случайных величин X и Y. Если 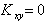, то можно говорить о том, что X и Y линейно независимы ( не коррелированны ).

Ковариационный момент 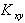характеризует разброс случайных величин X и Y относительно их средних. Если 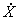мало, то и 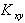также будет малым, хотя X и Y в достаточной мере коррелированны между собой.

Размерность 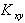не имеет физического смысла, что делает невозможным сравнение ковариационных моментов для двух пар случайных величин X и Y. Поэтому чаще всего используется нормированная величина 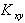, т.е. коэффициент корреляции

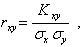(5.64)

где 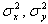- дисперсии X и Y; 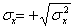и .

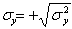Величина 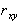безразмерная, кроме того она слабее, чем 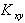, зависит от рассеяния X и Y, так как здесь 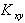нормируется делением на СКО X и Y от M[X] и M[Y].

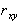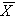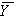Величину можно вычислить по выборке случайных величин X и Y. Допустим, что проведено n испытаний и при каждом отмечались значения случайных величин X, Y. Через и обозначим их среднее значения:

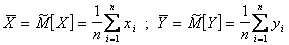(5.65)

где 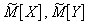- оценки математического ожидания X и Y.

Тогда выборочный коэффициент корреляции определяется по формуле

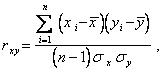(2.66)

где 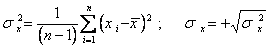; (5.67)

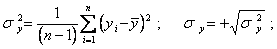(5.68)

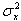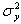, - выборочные дисперсии.

Уменьшение на единицу знаменателя в приведенных выше формулах связано с тем, что величины 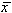и 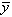, относительно которых берутся отклонения, сами зависят от объема выборки.

Для удобства вычислений и повышения точности расчетов преобразуем формулы (5.66), (5.67) и (5.68). Несложные преобразования их приводят к следующим формулам:

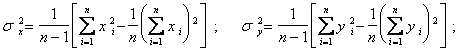(5.69)

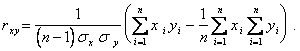(5.70)

Преимущество формул (5.69), (5.70) в том, что в них нет операций вычитания близких чисел, как в формулах (5.66) - (5.68), приводящих к потере точности вычислений. В формулах (5.69), (5.70) эта операция применяется только один раз.

Коэффициент корреляции не меняется от прибавления к X и Y каких - либо неслучайных слагаемых, от умножения X и Y на положительные числа. Если же одну из величин, не меняя другой, умножить на - 1, то на - 1 умножится и коэффициент корреляции.

Для независимых случайных величин 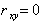, но 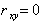может быть и для некоторых зависимых величин, которые при этом называются некоррелированными.

Коэффициент корреляции характеризует не всякую зависимость, а только линейную. Линейная вероятностная зависимость случайных величин X и Y заключается в том, что при возрастании X случайная величина Y имеет тенденцию возрастать ( при 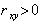) или убывать ( при 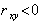) по линейному закону. Величина 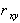характеризует степень тесноты линейной зависимости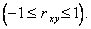

При 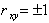величины X и Y связаны между собой линейной функциональной зависимостью, а при 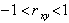связь между этими величинами стохастическая. При 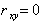между X и Y линейной корреляционной связи не существует, однако может существовать нелинейная регрессия.

Линейная регрессионная модель. Пусть с помощью коэффициента корреляции установлено, что зависимость между X и Y существует и она линейная, т.е.

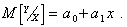(5.71)

Надо только определить коэффициенты 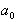и 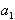. Определим их методом наименьших квадратов. Построим для этого функцию

,

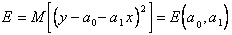где М - символ математического ожидания (усреднения на интервале ).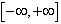

Для краткости записи обозначим 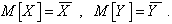Добавим к функции невязки 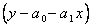слагаемое 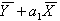и 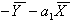получим

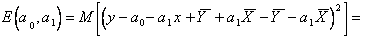
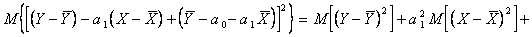
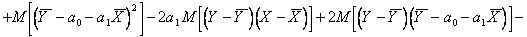
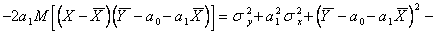
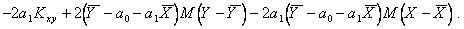
Так как 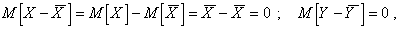получим

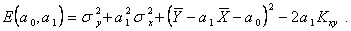(5.72)

Из необходимого условия минимума функции (5.72) 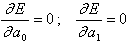получим следующую систему уравнений для определения :

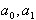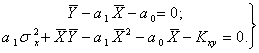(5.73)

Первое уравнение системы (5.73) умножим на 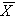и вычтем из него второе, получим

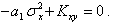
Отсюда находим

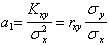. (5.74)

Из первого уравнения системы (5.73) определяем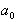

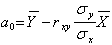. (5.75)

Линейная регрессионная модель имеет вид

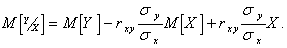(5.76)

Уравнение линейной регрессии, записанное в стандартном виде

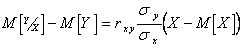(5.77)

наилучшим образом ( в смысле величины квадрата ошибок ) аппроксимирует зависимость условного среднего Y от X.

Если подставить 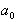и 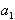в (5.72), то получим наименьшее значение суммы квадратов невязок

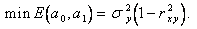(5.78)

Отсюда следует, что чем ближе 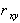к 1, тем лучше качество линейной аппроксимации, тем ближе к линиям регрессии расположены точки .

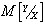Уравнение (5.77) позволяет прогнозировать среднее значение выхода Y для заданного значения входа X.

Теперь покажем, что 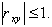Если X и Y связаны линейной функциональной связью, то 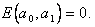Следовательно, 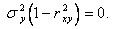Отсюда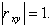

Учитывая, что всегда 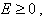то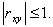

Нелинейная регрессионная модель одномерного объекта. Зададим уравнение регрессии полиномом степени m

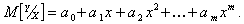(5.79)

Коэффициенты 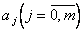можно определить методом наименьших квадратов. При этом, как правило, уравнение (5.79) наилучшим образом (в смысле минимума суммы квадратов невязок) аппроксимирует линию регрессии. Коэффициенты 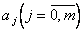не имеют статистической трактовки.

Для оценки силы связи X и Y в общем случае используется корреляционное отношение

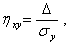(2.80)

где ;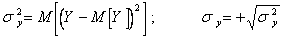

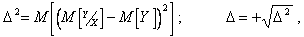
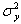- дисперсия Y относительно M[Y];

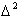- дисперсия линии регрессии 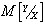, описываемой уравнением (5.79), относительно 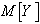. Величина 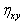равна отношению СКО 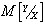от 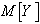к СКО Y от 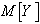(рис. 2.9). Причем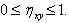

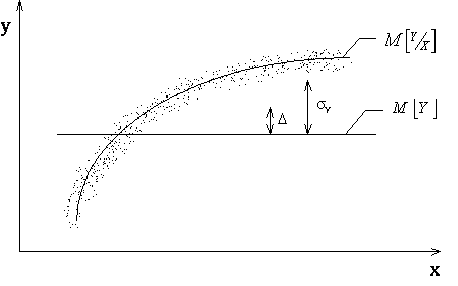
Рис. 2.9

Дисперсию 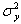можно представить суммой

,

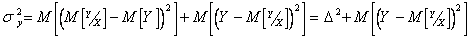Последний член характеризует разброс Y относительно 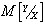. Отсюда находим

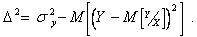(2.81)

Из (2.80) с учетом (2.81) имеем

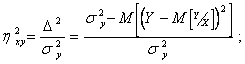
(2.82)

Если все значения Y лежат на линии регрессии, т.е. абсолютно точно удовлетворяют уравнению (2.79), тогда X и Y связаны функциональной связью и

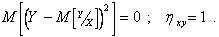
Теперь пусть Y не зависит от X, поэтому линия регрессии 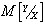совпадает с 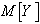и

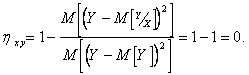
Чем меньше величина 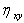, тем слабее связь между X и Y. Отметим, что при увеличении порядка полинома m, величина 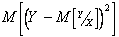будет убывать, а 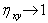, хотя, на самом деле, при зтом сила связи между X и Y остается неизменной. Трудность объективного выбора порядка m усложняет и использование корреляционного отношения 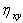для решения практических задач.

Множественная линейная регрессия. Множественная регрессия применяется для описания связи входных величин 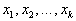и выходной случайной величины Y стохастического объекта. Обозначим условное математическое ожидание случайной величины Y при условии, что 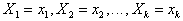через 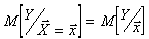, где

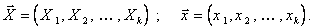
Уравнение линейной множественной регрессии имеет вид

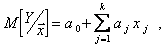(5.83)

где находятся методом наименьших квадратов:

(5.84)

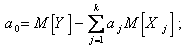(5.85)

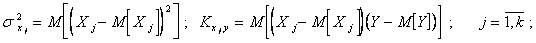
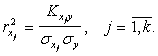
Оценки приведенных выше числовых характеристик случайных процессов можно определить по экспериментальным данным. Пусть в результате эксперимента имеем матрицу наблюдений

(5.68)

где n - количество опытов; 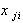- значение j - го входа в i - том опыте.

Тогда имеем следующие оценки характеристик

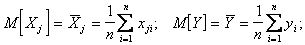
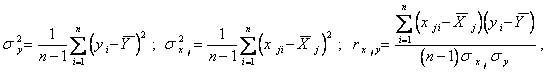
где всюду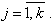

Коэффициенты 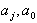получены при условии, что все входные воздействия линейно независимы, т.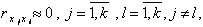е. где

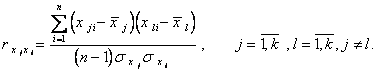
Рассмотрим общий случай, учитывая возможные связи между факторами (входами).

Перейдем от натурального масштаба к новому, проведя нормировку всех значений случайных величин по формулам:

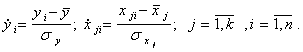(5.87)

При этом имеем исходный статистический материал в безразмерном масштабе:

В новом масштабе имеем:

.

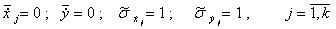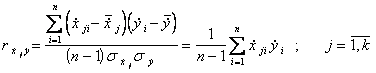
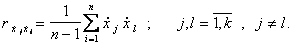
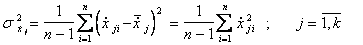
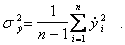
Вычисленные по этим формулам выборочные коэффициенты корреляции равны коэффициентам корреляции между переменными, выраженными в натуральном масштабе, т.е.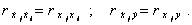

Уравнение регрессии между нормированными переменными не имеет свободного члена, т.к. 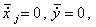и имеет вид

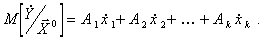(5.88)

Коэффициенты уравнения (5.88) находятся методом наименьших квадратов из условия:

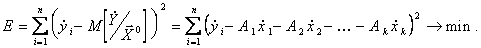
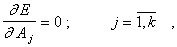
Которые дают следующую систему уравнений

(5.89)

где суммирование всюду осуществляется от 1 до n.

Умножим левую и правую части системы уравнений (5.89) на 1/(n-1). В результате при каждом коэффициенте 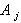получаются выборочные коэффициенты корреляции 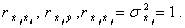С учетом этого, а также учитывая 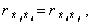получим

(5.90)

Решая систему линейных уравнений (5.90), находим 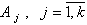. Если все входные воздействия линейно независимы, то 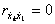и имеем: .

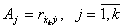Для изучения тесноты связи между функцией отклика Y и факторами 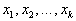используют коэффициент множественной корреляции R

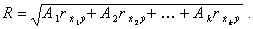(5.91)

Очевидно, что в случае линейно независимых входов

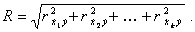(5.92)

R всегда положителен и принимает значение от 0 до 1. Чем больше R, тем лучше качество предсказаний данной моделью опытных данных.

От уравнения (5.88) можно перейти к уравнению (5.83) с переменными в натуральных масштабах, используя формулы (5.87) нормирования переменных входа :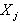

Нетрудно получить следующие формулы для пересчета коэффициентов модели:

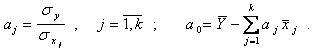
Нелинейная регрессионная модель многомерного объекта. Уравнение нелинейной регрессии стохастического многомерного объекта задается обычно полиномом

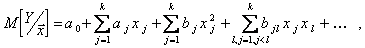(5.93)

где 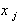- входные переменные объекта,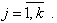

Коэффициенты уравнения (2.93), как правило, определяются методом наименьших квадратов. Наибольшие трудности вызывает структурная идентификация модели, т.е. выбор порядков полинома по каждому из входов, а также вычисление определителя плохообусловленной матрицы, часто встречающейся при идентификации коэффициентов модели.

Использование метода Брандона для построения уравнения множественной регрессии позволяет избежать эти трудности.

По этому методу уравнение регрессии записывается в виде

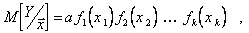(5.94)

где 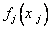- неизвестная функция переменной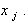

Порядок расположения факторов 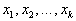в уравнении (5.94) не безразличен. Чем сильнее влияние на Y оказывает вход 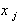, тем меньше должен быть порядковый номер индекса j. Это необходимо для повышения точности обработки результатов наблюдений.

Вид функции 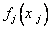выбирается при помощи построения эмпирических линий регрессии. Вначале по точкам выборки 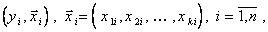строятся поле корреляции и эмпирическая линия регрессии 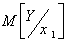(рис. 2.10).

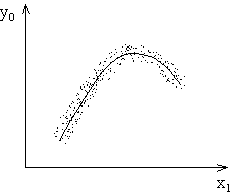
Рис. 2.10

По эмпирической линии регрессии определяется вид зависимости 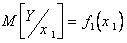и методом наименьших квадратов рассчитываются коэффициенты этого уравнения регрессии. Затем составляется выборка новой величины , где

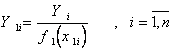(5.95)

Полученная величина 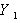не зависит уже от 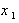,а определяется только параметрами 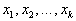. Поэтому можно записать

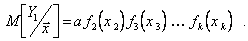(5.96)

По точкам новой выборки величин 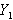и 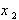вновь строятся корреляционное поле и эмпирическая линия регрессии, характеризующая зависимость 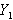от 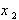(рис. 5.11):

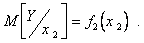(5.97)

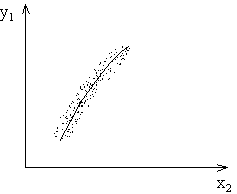
Рис. 2.11

Рассчитываются коэффициенты уравнения (5.97) и вновь составляется выборка новой величины 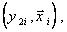где

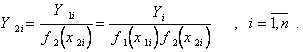(5.98)

Полученная величина 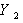не зависит уже от двух факторов 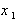и 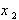и может быть определена из следующего уравнения регрессии:

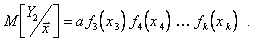(5.99)

Такая процедура определения функций 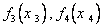и т.д. продолжается до получения выборки величины :

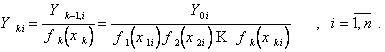(5.100)

Полученная величина 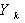не зависит от факторов 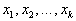и определяется коэффициентом исходного уравнения

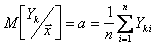(5.101)

где n - объем выборки.

Таким образом, окончательно получаем зависимость условного среднего выхода объекта Y от всех факторов (входов) 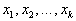, подставляя в уравнение (5.94) численное значение коэффициента 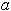и найденные выражения функций 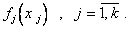Таким образом одновременно решаются задачи структурной и параметрической идентификации.

Оценка значимости коэффициентов и адекватности регрессионной модели. После того как уравнение регрессии найдено, необходимо провести статический анализ результатов. Он заключается в проверке значимости коэффициентов модели в сравнении с ошибкой воспроизводимости и оценке адекватности модели эксперименту. Такое исследование называется регрессионным анализом.

Оценку значимости коэффициентов модели выполняют по критерию Стьюдента. Для каждого проверяемого коэффициента 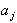вычисляют

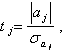(5.102)

где 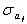- СКО j - го коэффициента.

Как правило, для получения дисперсии воспроизводимости проводится отдельная серия из m повторных опытов при фиксированных значениях входов. Пусть при этом получено 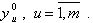Тогда дисперсия воспроизводимости определяется по формуле

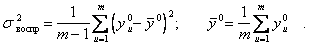(5.103)

Тогда

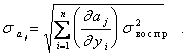(5.104)

Значения частных производных находят из выражения коэффициентов, найденных, например, методом наименьших квадратов.

Если 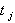больше табличного 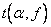(находят из таблицы распределения Стьюдента) для выбранного уровня значимости 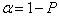(P - доверительная вероятность ) и числа степеней свободы 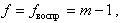то коэффициент 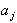значительно отличается от нуля.

Незначимые коэффициенты исключаются из уравнения регрессии. Оставшиеся коэффициенты пересчитываются заново, поскольку коэффициенты закоррелированы друг с другом.

Адекватность модели проверяется по F - критерию Фишера. Для этого вычисляют дисперсию адекватности

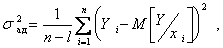(5.105)

где l - число коэффициентов модели, найденных по выборке объема n.

Определяют значение F - критерия 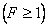по формуле

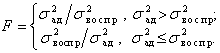(5.106)